Практическое занятие №9
Элементы синтеза систем управления
Цель: Получение практических навыков обеспечения заданных характеристик систем управления
1. Исходные теоретические сведения
1.1. Основные понятия
Под синтезом будем понимать проектирование регулятора системы управления по заданным к ней требованиям к статическим и динамическим свойствам. Эти свойства по-разному проявляются в различных режимах работы системы.
Процессы, протекающие в системе, представляемой моделью
описываются соотношением
.
Режим
отработки
начальных условий
– это процесс перехода из произвольного
начального состояния
в равновесное состояние при отсутствии
внешних воздействий на систему (
,
),
т.е. свободная составляющая процесса.
Этому процессу соответствует первое
слагаемое записанного выражения.
Режим
отработки
входа – это
процесс отработки входного воздействия
при
.
Этому процессу соответствует второе
слагаемое записанного выражения.
Режим
слежения за
входом –
это процесс отработки изменяющегося
входного воздействия
при нулевых начальных условиях и
отсутствии возмущений, т.е.
,
.
Этому процессу также соответствует
второе слагаемое записанного выражения.
Режим
отработки
возмущений
– это процесс отработки возмущений
при фиксированных начальных условиях
и входном воздействии. Этому процессу
соответствует третья составляющая
записанного выражения.
При
описании перечисленных процессов
используются временные (
и
)
характеристики, передаточные функции
(
и
)
и логарифмические частотные (амплитудная
и фазовая
)
характеристики.
Постановка задачи синтеза одноканальных систем. Одноканальный объект описывается передаточной функцией
.
Целью
функционирования замкнутой системы
управления является обеспечение с
заданной точностью ошибки управления
,
обеспечивающей выполнение условия
статики
.
Кроме того, должны быть обеспечены условия динамики, задаваемые обычно в виде оценок
и
.
При
этом управляемая переменная
является измеряемой
величиной, т.е. в цепь обратной связи
поступает не истинное, а измеренное ее
значение
,
так что реальной целью системы управления
является обеспечение условия
.
Таким образом, ошибка регулирования в соответствии с принципом суперпозиции есть сумма трех составляющих:
.
Первая (статическая ошибка по управлению) может быть скомпенсирована соответствующим выбором коэффициента усиления регулятора.
Вторая составляющая (ошибка по возмущению) является наиболее существенной и должна быть уменьшена до максимально допустимой величины:
.
Третья (ошибка измерения управляемой величины) в наибольшей степени проявляется в динамике (помеха измерения представляет собой высокочастотный сигнал).
Условия разрешимости задачи синтеза. К ним относятся:
– ограничение по ресурсам управления;
– устойчивость обратного объекта;
– управляемость и наблюдаемость объекта;
– вырожденность передаточной функции.
Ограниченность по ресурсам управления состоит в том, что сигнал управления должен иметь достаточную мощность для установления заданного значения управляемой переменной.
Полагая помеху измерения нулевой, можно представить уравнение выхода объекта в виде
.
Желаемый
вид управляемой переменной будет
обеспечен при условии формирования
желаемой передаточной характеристики
.
Он будет иметь вид
.
Из двух последних соотношений получаем необходимое «точное» управляющее воздействие в виде
.
Последнее соотношение носит название ресурсного ограничения. Его структурная интерпретация приведена на рис. 1.
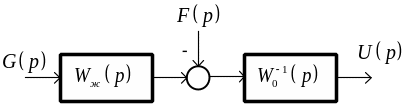
Рис. 1. Структурная интерпретация «точного» управления
Поскольку в реальных системах закон изменения возмущения неизвестен, то задача синтеза разрешима при условии, что
.
Требование
устойчивости
«обратного» объекта
основано на том, что согласно рис. 1 в
обеспечении управления участвует звено
с передаточной функцией
.
Если оно неустойчиво, то система
управления будет неработоспособной.
Это требование соответствует условию
,
т.е. условию отрицательности вещественных частей корней числителя передаточной функции системы.
Условия управляемости и наблюдаемости объекта используются при проверке разрешимости линейных систем, задаваемых в форме пространства состояний и здесь не рассматриваются.
Условие невырожденности передаточной функции состоит в том, что при наличии в передаточной функции системы одинаковых или близких сомножителей в полиномах числителя и знаменателя, т.е. при представлении ее в виде
в результате сокращения получается вырожденная передаточная функция
.
Система будет работоспособной, только если общие сомножители имеют корни с отрицательной вещественной частью. В этом случае удаление этих сомножителей не изменяет характеристик устойчивости системы. Отметим, что наличие в числителе и знаменателе сокращаемых множителей свидетельствует о наличии в системе неуправляемой или ненаблюдаемой частей.