1. 3 Расчёт критического уклона

Критическая глубина зависит только от геометрической формы поперечного сечения русла и расхода, но не зависит от продольного уклона дна .

При равномерном движении жидкости нормальная глубина, как это следует из формулы (1.1), зависит именно от уклона. Тогда очевидно, для русла, при заданном расходе , можно подобрать такое значение , при котором нормальная глубина станет равной критической , такой уклон обозначается через и называется критическим.

Таким образом критическим уклоном называется уклон, при котором нормальная глубина равна критической - .

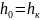Для определения нужно решить совместно уравнения (1.1), принимая , и (1.3), откуда

Нам известны:

м,

м².

Вычислим:

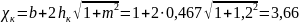м;

м;

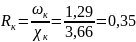м^0,5/с.

Теперь определим :

.

Так как , то 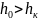и поток при равномерном движении будет находиться в спокойном состоянии.

1. 4 Определение вида кривой свободной поверхности потока

В зависимости от гидравлических условий, создающихся при возведении сооружений, и состояния потока глубины по его длине могут увеличиваться (кривая подпора) или уменьшаться (кривая спада).

Форма кривой свободной поверхности устанавливается на основе анализа дифференциального уравнения неравномерного движения третьего вида

, (1.4)

где , .

При этом тип кривой свободной поверхности зависит от зоны, в которой находится фиксируемая глубина

Равенство числителя нулю в уравнении (1.4), когда и при этом , соответствует равномерному движению. Если знаменатель стремится к нулю, то и свободная поверхность скачкообразно повышается (или понижается). В первом случае происходит переход потока из бурного состояния в спокойное – так называемый гидравлический прыжок, во втором – образуется водопад.

Когда числитель и знаменатель не равны 0, возможны различные сочетания знаков числителя и знаменателя. При глубина вдоль потока непрерывно и плавно увеличивается (кривая подпора), а при непрерывно и плавно уменьшается (кривая спада).

При неравномерном движении в русле с прямым уклоном ( ) различают три случая, характеризуемыми условиями:

и .

При этом получаем три возможные формы кривой свободной поверхности: кривые подпора , 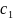и кривую спада .

и .

Здесь также получаем три возможные формы кривой свободной поверхности: кривые подпора , и кривую спада .

и .

Здесь получаем две возможные формы кривой свободной поверхности - кривые подпора , . В случае широкого прямоугольного русла, если считать, что коэффициент Шези не изменяется с глубиной ( ), кривые подпора превращаются в прямые горизонтальные линии.

Таким образом, вопрос о форме свободной поверхности решаем путём сопоставления фактической глубины потока с глубинами и :

В нашем случае и , значит в русле образуется кривая спада типа .

1. 5 Определение гидравлического показателя русла

Гидравлический показатель русла x введён Б.А. Бахметевым для упрощения связи между модулем расхода K и глубиной h. Вместо уравнения Шези он предложил зависимость:

, (1.5.1)

где и - две произвольно взятые глубины в данном поперечном сечении русла; и - соответствующие им расходные характеристики. Величина называется гидравлическим показателем русла. Приближённо считается, что он постоянен для данного поперечного сечения и не зависит от глубин.

Из зависимости (1.5.1) логарифмированием получена формула вычисления, м:

, (1.5.2)

Произведём расчёт:

, определим следующие характеристики при м:

м²,

м,

м,

м^0,5/с.

Теперь определим м³/с.

, определим следующие характеристики при м

м²,

м,

м,

м^0,5/с.

Теперь определим м³/с.7

И наконец гидравлический показатель русла:

.