
- •Лабораторная работа №2 статистическая обработка результатов измерений
- •Задание на подготовку к проведению лабораторной работы
- •Краткие теоретические сведения
- •Статистическая обработка результатов измерений
- •Косвенные измерения и обработка их результатов
- •Совместные измерения и их статистическая обработка
- •Контрольные вопросы
- •Описание лабораторной установки в комплект лабораторной установки входят:
- •Задание на лабораторную работу
- •Порядок выполнения работы
- •1. Проведение многократных измерений и выполнение их статистической обработки
- •Проведение измерений амплитудной характеристики усилителя и ее аппроксимация по методу наименьших квадратов
- •3. Измерение временных и амплитудных параметров сигналов с использованием осциллографа
- •Применение осциллографа как устройства сравнения
- •Содержание отчета
- •Приложение п.7.
Лабораторная работа №2 статистическая обработка результатов измерений
ЦЕЛЬ РАБОТЫ:
Закрепление навыков применения приборов общего назначения для проведения прямых и косвенных многократных измерений параметров радиосигналов и характеристик цепей.
Закрепление навыков проведения совместных измерений и обработки результатов по методу наименьших квадратов
Закрепление навыков применения универсального осциллографа для измерения амплитуд и временных параметров сигналов.
Задание на подготовку к проведению лабораторной работы
Изучить (по конспектам лекций, практических занятий и рекомендованной литературе) теоретический материал, соответствующий тематике лабораторной работы.
Допуск к лабораторной работе проводится в виде письменной работы с ответами на контрольные вопросы или в виде теста на ПЭВМ.
Изучить по данному руководству порядок выполнения работы и подготовить структуру отчета с указанием наименования работы, целей работы, пунктов экспериментальных исследований. В каждом пункте исследований привести схемы измерений, таблицы, координатные оси для построения графиков (масштабы выбираются исполнителем), Оставить место для расчетов и выводов.
Краткие теоретические сведения
Статистическая обработка результатов измерений
Анализ условий наблюдений и метода измерений, выявление возможных причин появления систематических погрешностей, принятие мер по их устранению.
Формирование выборки многократных наблюдений и ее предварительная обработка.
Результат измерения (оценка среднего значения результатов наблюдения), принимаемый за истинное значение измеряемой величины
![]() ,
(2.1)
,
(2.1)
где хi – результат i - го измерения; n – количество измерений.
Оценка СКО наблюдений (характеристика точности наблюдений)
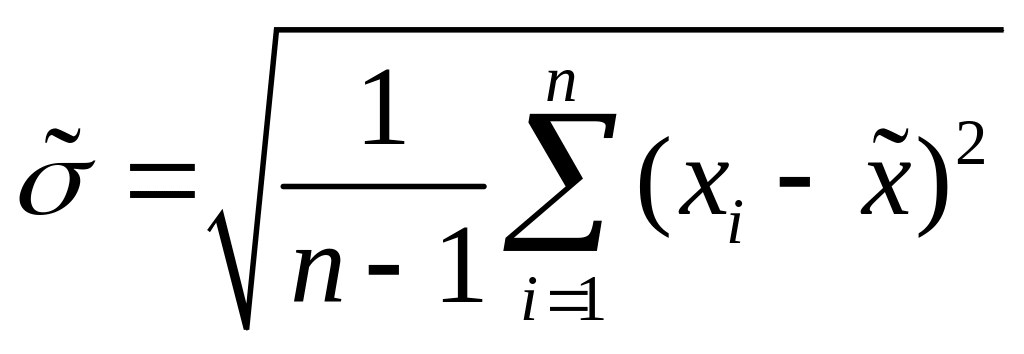 .
(2.2)
.
(2.2)
Оценка СКО результата измерения (характеристика точности результата измерений)
![]() .
(2.3)
.
(2.3)
Определение промахов и их отбрасывание. Результаты упорядочиваются по возрастанию. При неизвестном законе распределения погрешностей для крайних значений рассчитываются коэффициенты
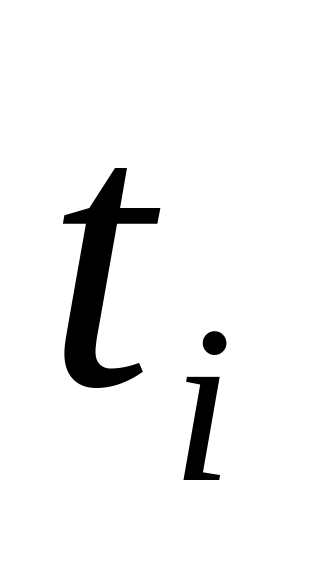 ,
которые сравниваются с коэффициентом
tГ
,
которые сравниваются с коэффициентом
tГ
![]() .
.
![]() .
.
Коэффициент
![]() определяется
по табл.
П. 1,
исходя из числа наблюдений и заданного
уровня значимости q
(обычно
задается 0,05 или 0,025). Если закон
распределения погрешностей нормальный,
то для крайних значений выборки
производится сравнение
определяется
по табл.
П. 1,
исходя из числа наблюдений и заданного
уровня значимости q
(обычно
задается 0,05 или 0,025). Если закон
распределения погрешностей нормальный,
то для крайних значений выборки
производится сравнение
![]() ,
,
![]() .
.
Если условия выполняются, то промахов нет.
Промахи отбрасываются из результатов наблюдений, после чего производится повторное вычисление характеристик выборки по формулам (2.1) – (2.3).
Определение доверительной границы случайной погрешности результата измерения по заданной доверительной вероятности (как правило, РД = 0,95).
задаются доверительной вероятностью PД;
при
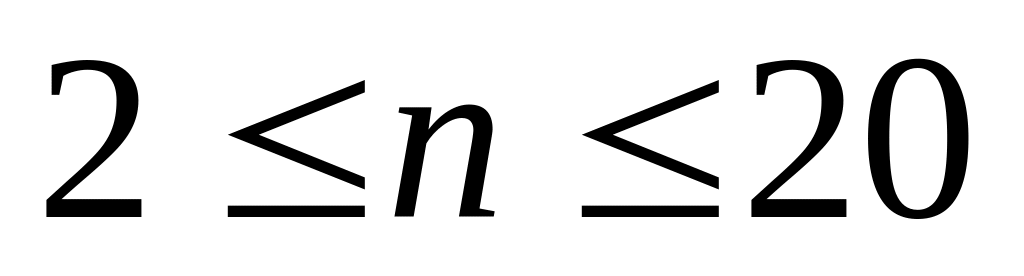 используется
распределение Стьюдента, при n
> 20
– нормальный закон распределения;
используется
распределение Стьюдента, при n
> 20
– нормальный закон распределения;при n < 20 по заданным n и PД из табл. П. 5 находят коэффициент t(PД, n) и определяют доверительную границу случайной погрешности
![]() ;
(2.4)
;
(2.4)
при n > 20 по заданному значению PД из таблицы
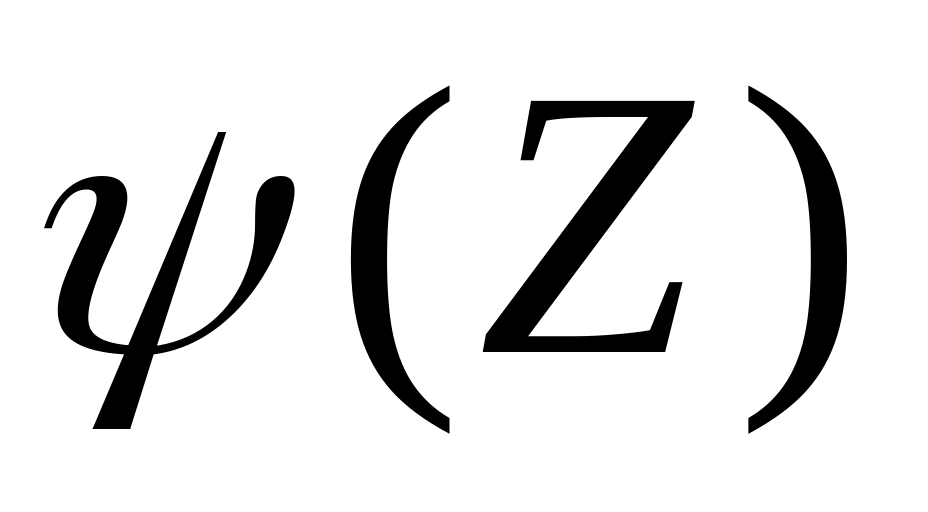 (табл.
П. 6)
находят
Z,
соответствующее условию
(табл.
П. 6)
находят
Z,
соответствующее условию
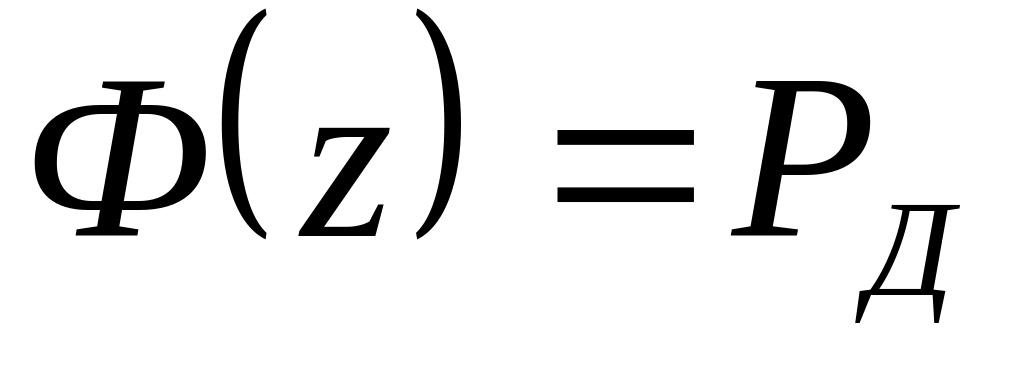 ,
и
определяют
,
и
определяют
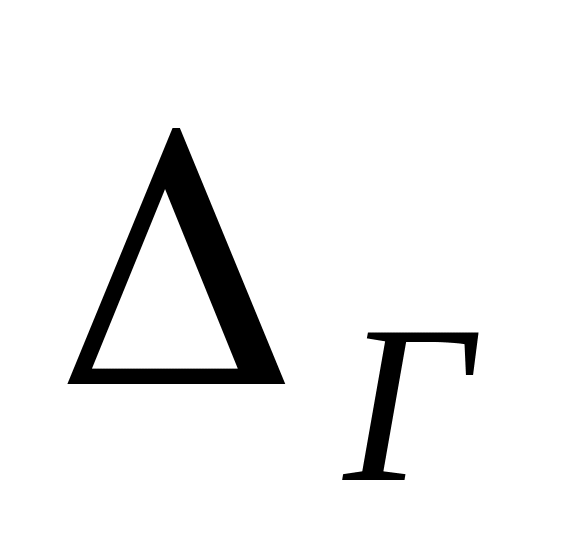 ;
;
![]() ;
(2.5)
;
(2.5)
результат представляется в виде
![]() .
(2.6)
.
(2.6)
1.5. Оценивание границ θi каждой из НСП. В качестве границы каждой НСП, как правило, принимаются пределы допускаемых основных и дополнительных погрешностей средств измерения.
Общую границу совокупности НСП определяют по правилу
![]() ,
(2.7)
,
(2.7)
где коэффициент k находится по специальным графикам или таблицам по значениям доверительной вероятности РД и количеству m неисключенных систематических погрешностей (методика определена ГСИ).
1.6.
Правило оформления результата с учетом
границ НСП. Если
![]() ,
то отбрасываются НСП (их влияние на
погрешность измерений малозначительно).
Если
,
то отбрасываются НСП (их влияние на
погрешность измерений малозначительно).
Если
![]() ,
то отбрасываются случайные погрешности
(их влияние малозначительно), если
,
то отбрасываются случайные погрешности
(их влияние малозначительно), если
![]() ,
то общая граница доверительного интервала
определяется в виде
,
то общая граница доверительного интервала
определяется в виде
![]() .
.
2. Проверка гипотезы о нормальном законе распределения погрешностей результатов наблюдения (промахи отброшены). Выполняется в последовательности:
вычисляют значение смещенной оценки СКО наблюдений
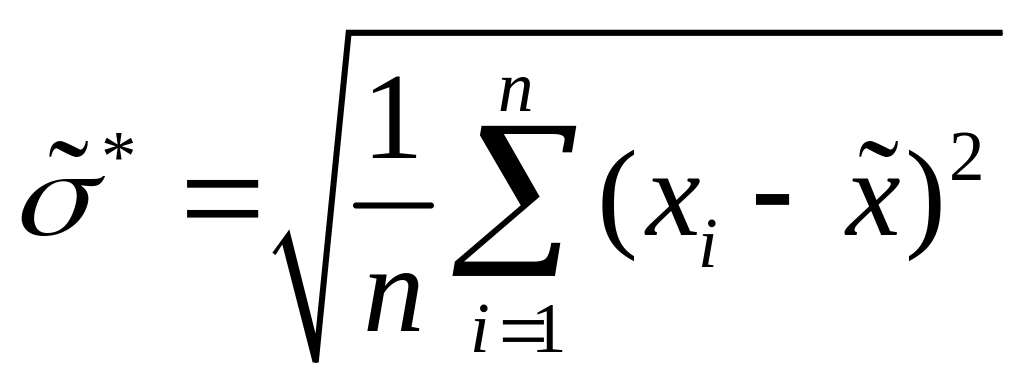 ;
(2.8)
;
(2.8)
вычисляют значения параметра
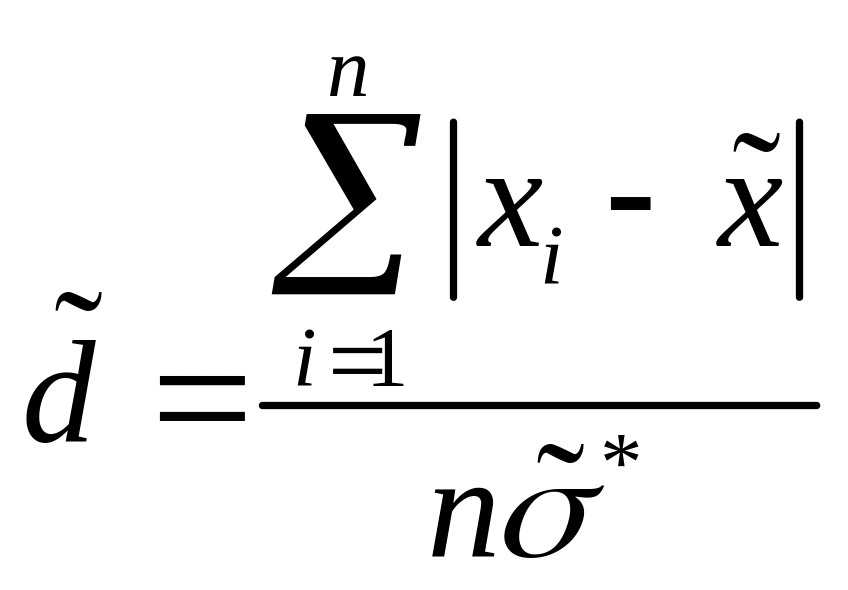 (2.9)
(2.9)
по заданному уровню значимости критерия 1 q1 (обычно q1 = 0,02 или q1 = 0,1) и числу измерений n по табл. П. 2 находят параметры dmin и dmax.
Формула для линейной интерполяции (если число измерений находится между табличными значениями):
![]() ,
,
где n – число измерений; n0, n1 – ближайшее меньшее и большее число измерений, указанное в таблице. Параметр dn определяется отдельно для минимальных ( dmin ) и максимальных (dmax) значений.
При
выполнении условия
![]() принимают
гипотезу о нормальном распределении
по первому критерию;
принимают
гипотезу о нормальном распределении
по первому критерию;
по заданному уровню значимости критерия 2 q2 (0,01, 0,02 или 0,05) и числу наблюдений из табл. П. 3 находят значения вероятности P и коэффициента m.
по величине P/2 из табл. П.4 интеграла вероятностей из уравнения
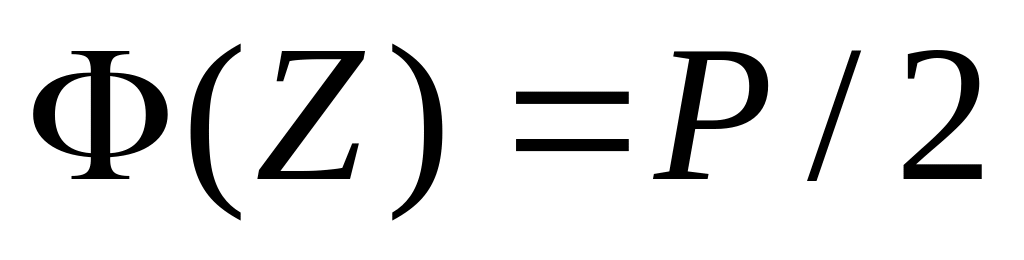 находят аргумент Z
= ZP/2
и рассчитывают коэффициент
находят аргумент Z
= ZP/2
и рассчитывают коэффициент
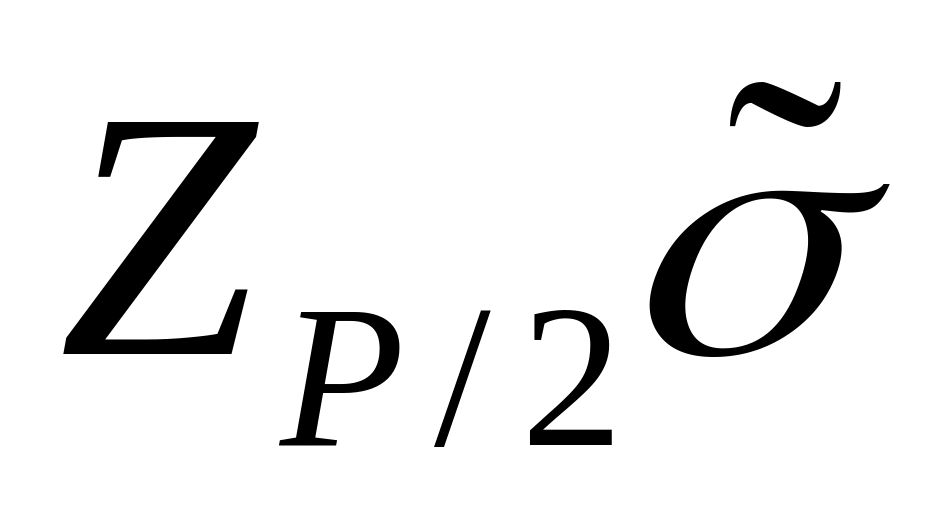 ;
;подсчитывают число mэ модулей погрешностей, которое должно удовлетворять условию
![]() .
.
Если mэ < m, то принимается гипотеза о нормальном законе распределения по второму критерию.
Гипотеза о нормальном законе распределения результатов наблюдения принимается, если выполняются условия обоих критериев.
