4 Приклад роботи програмного комлексу

Проаналізуємо роботу програмного комплексу на прикладі. Задамо у програму логічний вираз, що можна побачити на скріншоті головного вікна на рисунку 4.1.

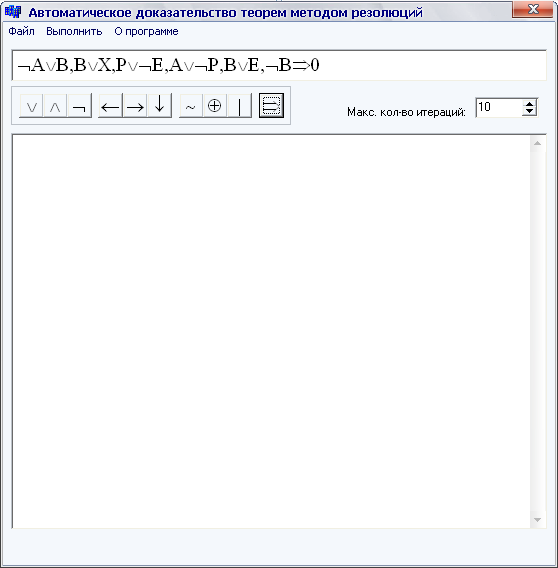
Рис. 4.1 – Головне вікно програми з введеними початковими даними

Після виконання розрахунків, отримано результат, що показаний на рисунку 4.2 – доказ отримано за 38 кроків, що є безперечно занадто великою кількістю кроків для такого малого вхідного виразу, але це є недоліком автоматичного доказу - програма користується повним перебором значень для отримання доказу.

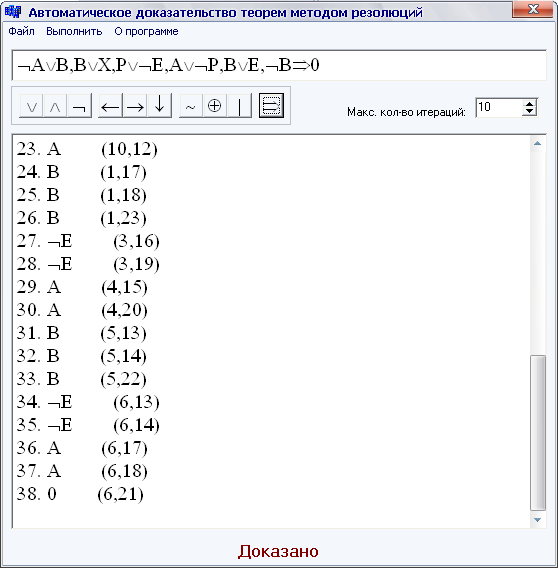
Рис. 4.2 – Результат доказу

Приведемо всі етапи обчислень, що провів програмний комплекс для отримання доказу (розділення на діз’юнкти, склеювання всіх можливих діз’юнктів):













































































Приведемо ще один приклад роботи програми. Візьмемо логічний вираз, показаний на скріншоти на рисунку 4.3.

При встановленні різних показників максимальної кількості ітерацій доказ все одно не знаходиться, тобто є підстави казати, що поданий логічний вираз не є істинним. Програма не може знайти таку склейку серед всіх можливих диз’юнктів, яка б привела до результату 0, який би означав доведення виразу.

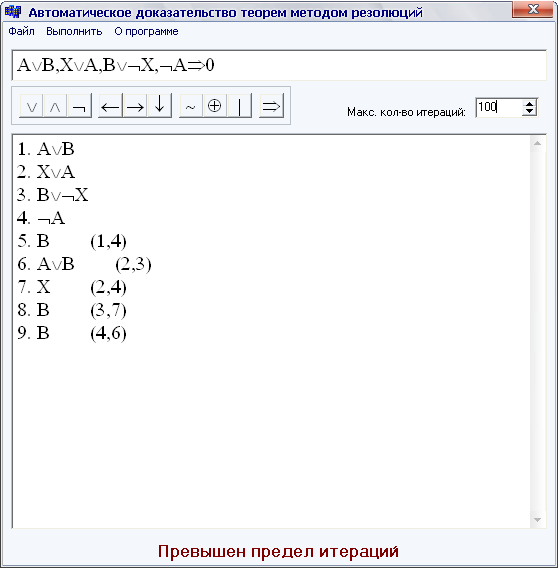
Рис. 4.3 – Відсутність доказу за дане число ітерацій

ВИСНОВКИ

1. В роботі розглянуто метод резолюцій для автоматичного доказу теорем математичної логіки.

2. За допомогою методу резолюцій реалізовано програмний комплекс, який визначає істинність введеного логічного виразу..

3. Програмний комплекс з позитивним результатом протестовано на різноманітних вхідних даних, в тому числі на задачах, що є важковирішуваними «ручними» методами.

4. Програму рекомендовано для використання як інструмент для автоматичного доказу істинності логічних виразів у практичному використанні, а також у якості демонстрації можливостей застосування комп’ютерної техніки для рішення задач математичної логіки.

Перелік посилань

1. Акимов О.Е. Дискретная математика: логика, группы, графы. 2-е изд., дополн. М.: Лаборатория Базовых Знаний, 2001 – 376 с.: ил.

2. Горбатов В.А. Основы дискретной математики.- М.: Высш. шк., 1986

3. Бардачов Ю.М. Дискретна математика. – Київ, Вища школа, 2002

4. Новиков Ф.А. Дискретная математика для программистов – СПб: Питер, 2000. – 304 с.: ил.

5. Донской В.И. Дискретная математика. – Сімферополь, Сонат, 2000

RESUME

An object of work is automatic proof of theorems after the method of resolutions.

A purpose of work is development of programmatic complex for realization of automatic proof of theorems after the method of resolutions.

A programmatic complex is developed by a programming of Borland C++ Builder environment. Created a programmatic complex allows for the set boolean expression to define his truth or fallaciousness with presentation of all intermediate calculations at leading to.

The program is made to order for the use in higher educational establishments in quality the example of automatic implementation of proof of theorems after the method of resolutions, and also as the applied instrument for work from proof of boolean expressions.