ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Транспорт и хранение нефти и газа»

«Массовые расходомеры»

Реферат по дисциплине

«Физические основы учета

нефти и газа при технических операциях»

Выполнил ст. гр. ГТ-08-01 С.М. Чижков

Проверил доктор наук С.В. Китаев

Уфа - 2010

Введение

В связи с развитием рыночной экономики возникает необходимость реорганизации системы учета сырьевых и продуктовых потоков. Все потоки по своему типу, например на нефтеперерабатывающем заводе можно разделить на: входящие (сырье на завод), внутрицеховые, межцеховые, выходящие (продукция с завода).

Возрастающие требования к качеству измерения расхода на узлах коммерческого учета вызывают необходимость замены ряда устаревших приборов на более современные. Причем они должны удовлетворять ряду качественных критериев: измерение массового расхода, измерение плотности, измерение температуры, наличие компьютерного интерфейса, удобство монтажа и эксплуатации.

Приборы, отвечающие этим требованием, относятся к прямому методу измерения массы продукта.

Таким прибором является кориолисов массовый расходомер. Он обладает точностью выше, чем все остальные расходомеры, имеет ряд преимуществ перед объемными расходомерами. В первую очередь это измерение массового расхода напрямую. Это особенно важно на химическом производстве, где необходим точный учет жидкостей.

Измерение массового расхода исключает необходимость в переводе объемного расхода в массовый, путем вычисления.

Рассмотрим подробно понятия и явления и законы, лежащие в основе принципа действия прибора.

Физические основы принципа действия кориолисова расходомера

Скорость

Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и т.п.

Пусть материальная точка (в дальнейшем – частица) переместилась вдоль некоторой траектории из точки 1 в точку 2. Расстояние между точками 1 и 2, отсчитанное вдоль траектории, называется путем, пройденным частицей. Мы будем обозначать его буквой s.

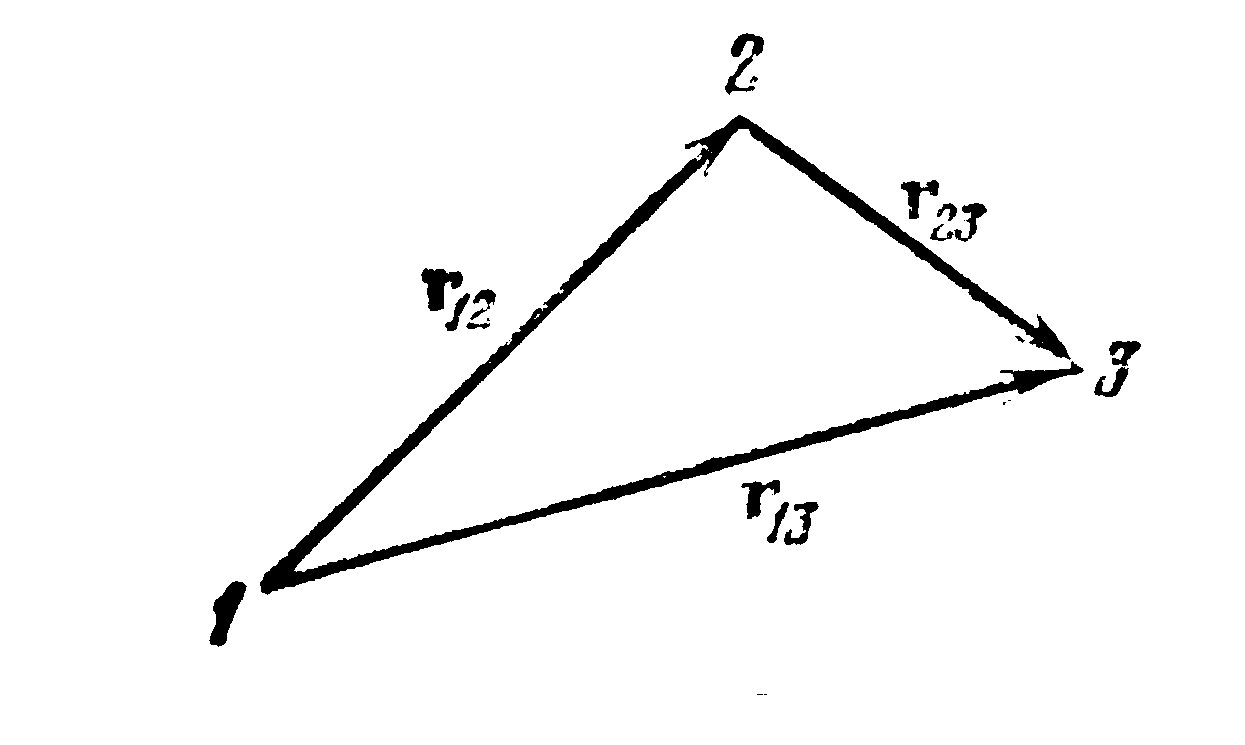Прямолинейный отрезок, проведенный из точки 1 в точку 2, называется перемещением частицы. Обозначим его символом r₁₂. Предположим, что частица

совершает последовательно два перемещения: r₁₂ и r₂₃. Суммой этих перемещений естественно назвать такое перемещение r₁₃, которое приводит к тому же результату, что и первые два перемещения вместе.

Таким образом, перемещения характеризуются численным значением и направлением и, кроме того, складываются по правилу параллелограмма. Отсюда следует, что перемещение есть вектор.

В обыденной жизни под скоростью понимают путь, проходимый частицей за единицу времени. Если за равные, сколь угодно малые промежутки времени частица проходит одинаковые пути, движение частицы называют равномерным. В этом случае скорость, которой обладает частица в каждый момент времени, можно вычислить, разделив путь s на время t.

В физике под скоростью понимают векторную величину, характеризующую не только быстроту перемещения частицы по траектории, но и направление, в котором движется

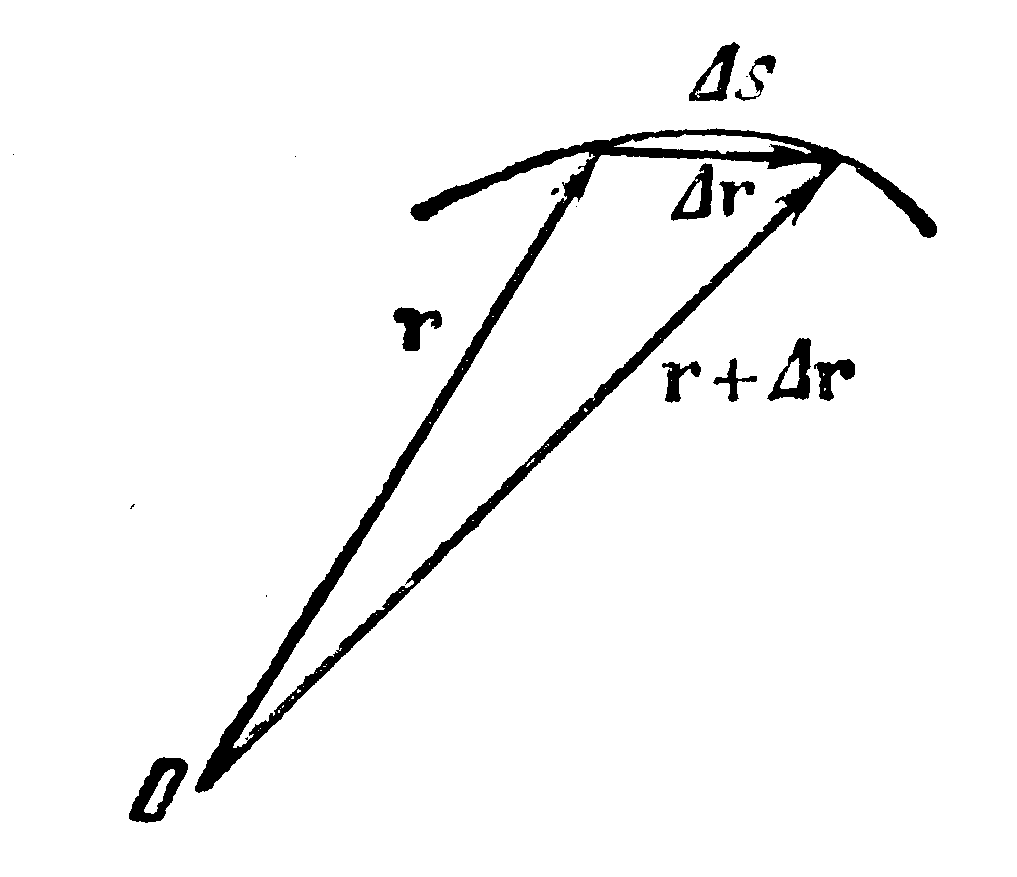
частица в каждый момент времени. Разобьем траекторию на бесконечно малые участки длины ds. Каждому из участков сопоставим бесконечно малое перемещение dr.

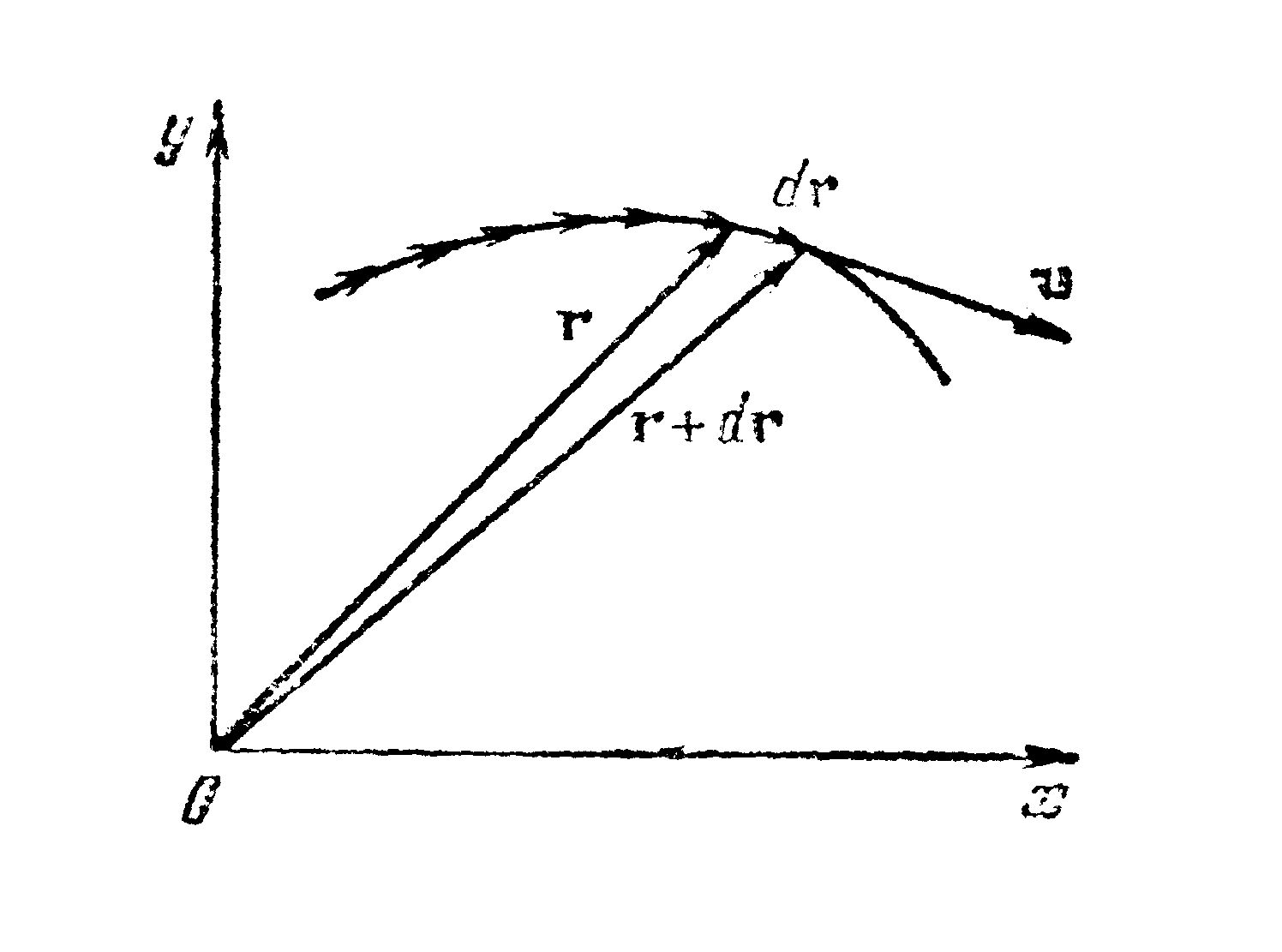
Разделив это перемещение на соответствующий промежуток времени dt, получим мгновенную скорость в данной точке траектории:

Таким образом, скорость есть производная радиуса-вектора частицы по времени. Перемещение dr совпадает с бесконечно малым элементом траектории. Следовательно, вектор v направлен по касательной к траектории.

Рассуждая более строго, для получения формулы мгновенной скорости нужно поступить следующим образом. Зафиксировав некоторый момент времени t, рассмотрим приращение радиуса-вектора Dr, за малый промежуток времени Dt, следующий за t. Отношение Dr/Dt среднее значение скорости за время Dt. Если брать все меньшие промежутки времени Dt, отношение Dr/Dt в пределе даст значение скорости v в момент времени t:

Найдем модуль этого выражения, т.е. модуль скорости v:

В этой формуле нельзя написать Dr вместо |Dr|. Вектор Dr есть по существу разность двух векторов (r в момент времени t+Dt минус r в момент времени t). Поэтому его модуль можно записать только с помощью вертикальных черточек. Символ |Dr| обозначает модуль приращения вектора r, в то время как Dr представляет собой приращение модуля вектора r: D|r|. Обе эти величины, вообще говоря, не равны друг другу:

В этом можно убедиться на следующем примере. Пусть вектор r получает такое приращение Dr, что модуль его не изменяется: |r+Dr|=|r|. Тогда приращение модуля вектора равно нулю (D|r|=Dr=0). В то же время модуль приращения вектора r, т.е. |Dr|, отличен от нуля. Сказанное справедливо для любого вектора a: в общем случае |Da| не равно Da. Видно, что путь Ds, вообще говоря, отличен по величине от модуля перемещения Dr. Однако, если брать отрезки пути Ds и перемещения Dr, соответствующие все меньшим промежуткам времени Dt, то различие между Ds и |Dr| будет убывать и их отношение в пределе станет равным единице:

Н а этом основании можно заменить |Dr| через Ds, в результате чего получится выражение:

Таким образом, модуль скорости равен производной пути по времени.

Очевидно, что величина, называемая в обыденной жизни скоростью, на самом деле представляет собой модуль скорости v. При равномерном движении модуль скорости остается неизменным (v=const), в то время, как направление вектора v, изменяется произвольным образом ( в частности, может быть постоянным).