Задача №1

В поток воздуха, двигающегося по трубе с числом М = 0,8 и температурой торможения Т^* = 700 К, ввели легкий небольшой предмет. Какова будет температура предмета после установления теплового равновесия?

Решение:

Температура тела, помещенного в поток после установления теплового равновесия, будет равна статическому давлению воздуха, т.е.:

Ответ: .

Задача №2

По трубе диаметром 400 мм движется идеальная жидкость со средней скоростью 5 м/сек. Как изменятся скорость движения на участке трубопровода с диаметром 250 мм?

Решение:

Из условия задачи ясно, что G = const. Зная формулу расхода , можем приравнять расход для первого и второго сечений и выразить из полученного соотношения искомую скорость:

Ответ:

Задача №3

Вертикальная труба диаметром 0,7 м и высотой 15 м заполнена водой. Какова величина потенциальной энергии жидкости, если за линию отсчета уровней принять основание вертикальной трубы?

Решение:

Потенциальная энергия вычисляется по формуле:

, причем .

Тогда получаем

.

Ответ: .

Задача №4

Сооружаемая на реке ГЭС будет иметь мощность 6,3·10⁶ кВт. Определять расход воды через турбины гидростанции при напоре 200 м и КПД турбины 0,96.

Решение:

Мощность турбины можно выразить формулой:

.

Тогда можем вычислить расход воды как

.

Ответ:

Задача №5

Трубопровод переменного сечения смонтирован в вертикальной плоскости. В сечении 1–1 трубопровод имеет d₁ = 150 мм и р₁= 1,11 бар. Сечение 2–2 находится выше сечения 1–1 на 7 м и имеет d₂ = 250 мм, а р₂ = 1 бар. По трубопроводу перекачивается Трубопровод переменного сечения смонтирован в вертикальной керосин с плотностью ρ = 830 кг/м³. Определить, в каком направлении движется жидкость по трубопроводу при расходе Q = 0,2 м³/с.

Решение:

Уравнение Бернулли для идеальной несжимаемой жидкости имеет вид:

.

Предположим, что жидкость движется сверху вниз. Тогда ; ; ; ; . В данном случае направление течения совпадает с направлением действия силы тяжести, то есть силы тяжести совершают положительную работу, чему соответствует увеличение энергии единицы массы. Поэтому член в уравнении Бернулли может быть положительным только при . В результате расчеты по уравнению Бернулли приводят к следующему:

.

Следовательно, первоначальное предположение противоречит уравнению Бернулли и должно быть отклонено.

Примем противоположное предположение: жидкость движется снизу вверх. Тогда ; ; ; ; . В данном случае направление течения противоположно направлению действия силы тяжести, поэтому ускорение свободного падения должно быть взято с противоположным знаком, то есть . В результате расчеты по уравнению Бернулли приводят к тождеству:

.

Ответ: жидкость движется снизу вверх.

Задача №6

По трубопроводу перекачивается жидкость с плотностью ρ = 800 кг/м³. В сечения 1–1 диаметр трубопровода d₁ = 150 мм, а в сечении 2–2, расположенном на 6 м выше сечения 1–1, диаметр d₂ = 300 мм и давление р₂ = 1,5 бар. Определить, какое должно быть давление р₁, если жидкость движется снизу вверх, а в другом случае сверху вниз при одинаковом расходе Q = 0,2 м³/с.

Решение:

Уравнение Бернулли для идеальной несжимаемой жидкости имеет вид:

.

В первом случае, при движении жидкости снизу вверх, давление рассчитываем следующим образом:

Во втором случае, при движении сверху вниз, давление будет равно:

Ответ: при движении снизу вверх ; при движении сверху вниз .

Задача №7

Какова потеря удельной энергии потока жидкости (в джоулях на кг) при внезапном расширении трубопровода от d₁ = 500 мм до d₂ = 750 мм. Расход жидкости 2 м³/с.

Решение:

Ответ:

Задача №8

Самолет летит па высоте 11 км. Прибор, замеряющий число М полета, показал, что М = 0,9. Определить скорость полета самолета и температуру торможения, считая внешние условия стандартными.

Решение:

Из определения числа Маха следует, что .

Скорость звука находим как

Тогда полная температура равна

Ответ:

Задача №9

На высоте 15 км скорость полета самолета оказалась 2500 км/ч. Определять число М полета и температуру торможения, считая внешние условия по МСА.

Решение:

Число Маха рассчитывается по формуле: , причем

, где на высоте 15000 м.

Тогда получаем: , .

Температуру торможения выразим из соотношения

.

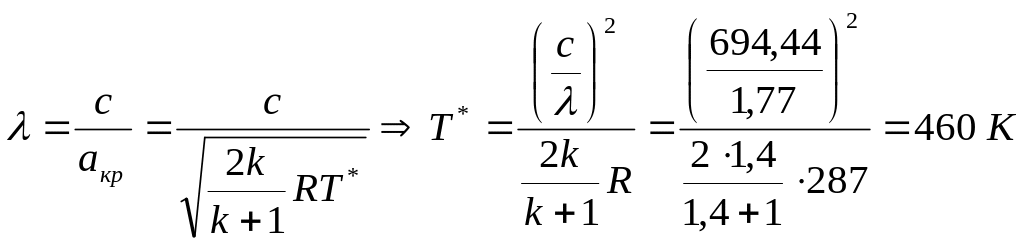Ответ: .

Задача №10

Самолет летит на высоте 6000 м. Насадок полного давления, установленный на самолете, показал давление 681 мм рт. ст. Какова скорость самолета и насколько ее надо увеличить, чтобы лететь со скоростью, равной скорости звука на этой высоте? Внешние условия стандартные.

Решение:

На высоте . Тогда . При этом . Следовательно, самолет летит со скоростью, которая больше скорости звука. , . Полет со скоростью, которая равна скорости звука . Значит, скорость полета надо уменьшить на .

Ответ: нужно уменьшить скорость на .

Задача №11

Определить скорость истечения и расход воздуха из воздухопровода заводской воздушной магистрали через сужающийся насадок площадью 3,14 см². Полное давление в магистрали 50 Н/см², а температура .

Решение: Скорость истечения рассчитываем по формуле:

.

Расход воздуха: .

Ответ: ; .

Задача №12

Лемнискатный насадок для замера расхода воздуха установлен на входе в газотурбинный двигатель (рис. 3). Определить расход и скорость воздуха в мерном насадке, если водяной манометр показал перепад давления , диаметр насадка 400 мм, а внешние условия стандартные (В₀ = 760 мм рт. ст.; Т = 288 К).

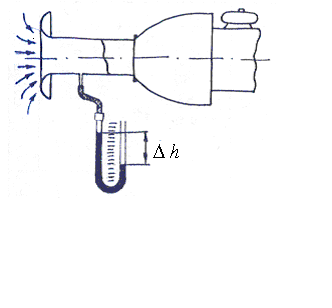
Лемнискатный насадок на входе в аэродинамическую трубу

Решение:

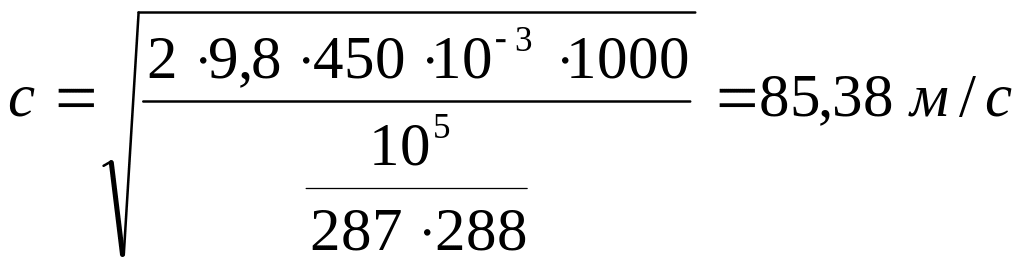Поскольку жидкость несжимаема, запишем для нее уравнение Бернулли: . Также можем записать: . Плотность равна: . Расход можем найти по формуле: . Получаем . Тогда, объединив все формулы, находим искомый расход воздуха в мерном насадке: .

Ответ: