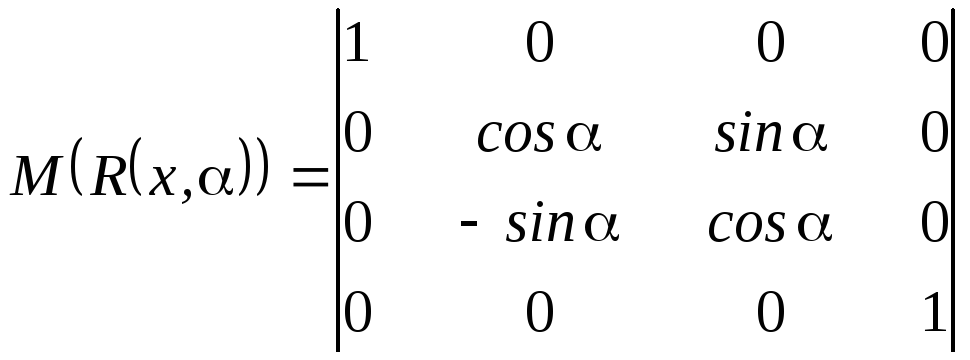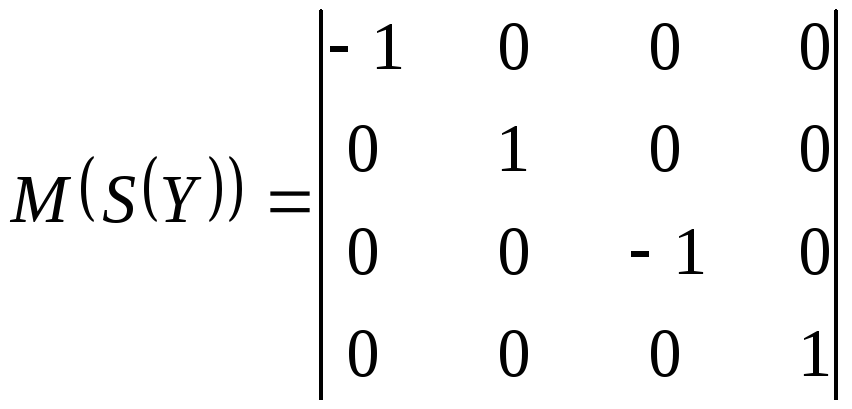55

3.Геометрические преобразования в пространстве

3.1.Основные геометрические преобразования

В общем случае преобразование вектора P (x, y, z, 1) в вектор P’(x’, y’, z’, 1) можно представить в виде

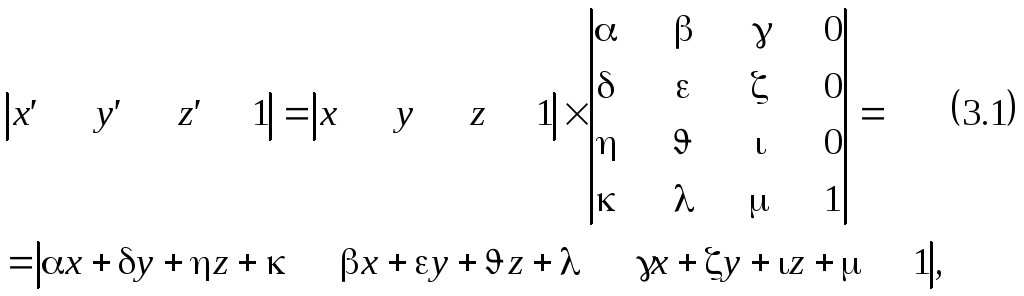
где - элементы матрицы трехмерного геометрического преобразования, которые необходимо определить для реализации требуемого действия. Определение этих элементов возможно двумя способами:

• геометрическое преобразование, примененное к объекту или совокупности объектов, может быть композицией (последовательностью) нескольких преобразований. Для его описания используется матрица, представляющая собой произведение матриц более простых преобразований (следствие ассоциативности матричного умножения), каждая из которых должна быть сведена к цепочке (произведению) описанных ниже элементарных преобразований, элементы матриц которых имеют явный геометрический смысл;

• для требуемого геометрического преобразования известны исходный и преобразованный объекты. В этом случае производится решение уравнения (3.1) относительно элементов матрицы.

К основным трехмерным геометрическим преобразованиям относятся:

• преобразование переноса на вектор T (t_x, t_y, t_z);

• преобразование гомотетии (масштабирования) относительно начала координат на вектор E(e_x, e_y, e_z);

• преобразования поворотов вокруг оси абсцисс на угол , вокруг оси ординат на угол, вокруг оси аппликат на угол;

• преобразование центральной симметрии относительно начала координат;

• преобразования осевой симметрии относительно осей абсцисс, ординат и аппликат;

• преобразования зеркальной симметрии относительно плоскостей XOY, YOZ и XOZ.

В табл.3.1приведены матрицы этих преобразований. Легко заметить, что реально матриц основных геометрических преобразований не 12, как в табл.3.1, а 8. Это связано с тем, что матрицы преобразований осевой симметрии являются матрицами преобразований поворота вокруг соответствующей координатной оси на угол 180 градусов, а матрица центральной симметрии относительно начала координат является произведением матриц преобразований зеркальной симметрии относительно всех трех координатных плоскостей.

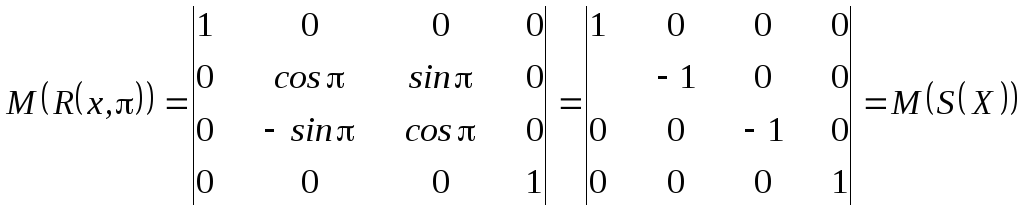
Табл.3.1.Матрицы основных трехмерных геометрических преобразований

Перенос на T (tx, ty, tz)	Гомотетия на E (ex, ey, ez)
Вращение вокруг оси абсцисс на угол	Вращение вокруг оси ординат на угол
Вращение вокруг оси аппликат на угол	Центральная симметрия относительно начала координат
Осевая симметрия относительно оси абсцисс	Осевая симметрия относительно оси ординат
Осевая симметрия относительно оси аппликат	Зеркальная симметрия относительно плоскости X0Y
Зеркальная симметрия относительно плоскости X0Z	Зеркальная симметрия относительно плоскости Y0Z

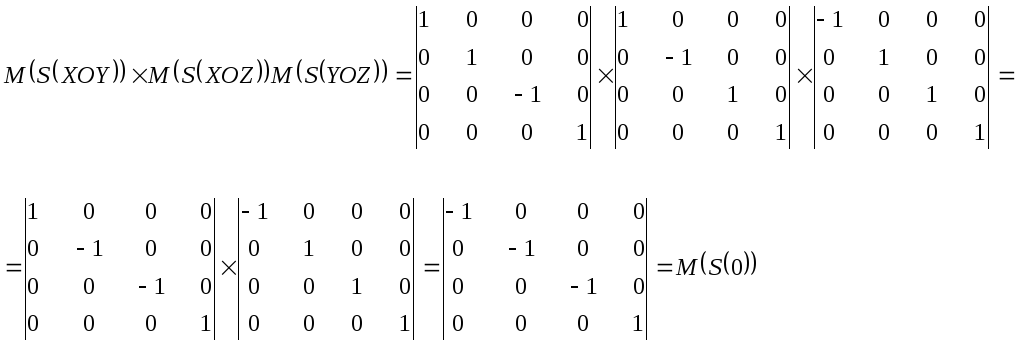
Определители всех матриц (табл.3.1), за исключением матрицы M(E), тождественно равны 1. Физическое объяснение этого факта заключается в том, что при этих преобразованиях соблюдается постоянство объема моделируемого объекта. Выполнение этого условия для преобразования гомотетии возможно при соблюдении следующего соотношения

e_x e_y e_z = 1.

Постоянство объема при трехмерных геометрических преобразованиях накладывает общее ограничение на элементы матрицы полного преобразования в виде равенства 1 ее определителя:

что дает следующее уравнение, связывающее элементы матрицы:

Матрицы двумерных преобразований могут быть получены из соответствующих матриц трехмерных преобразований исключением третьих строки и столбца (элементов, связанных с координатой по оси аппликат).

Реализация геометрических преобразований применительно к конкретной геометрической модели заключается в последовательном перемножении каждого вектора-строки дескриптора вершин S(X,Y,Z), дополненного до однородных координат S(X,Y,Z,1), на необходимые матрицы преобразований. Полученный в результате дескриптор вершин будет содержать координаты преобразованной модели.