Формальная постановка задачи
Рассмотрим задачу о защите посевов при
наличии наблюдений за погодными явлениями
и прогнозных значений, предоставляемых
метеобюро. В качестве возможных состояний
природы будем рассматривать множество
состояний
,
где
- наблюдаются заморозки,
- заморозков не наблюдается. Прогнозные
значения описываются множеством
,
где
- прогнозируются заморозки,
- прогнозируются теплая погода. Множество
решений
включает в себя два возможных решения
,
где
- решение защищать посевы от заморозков,
- решение не защищать посевы от заморозков.
Запишем задачу в терминах потерь, т.е. определим потери от принимаемых решений при различных состояниях природы (см. таблицу ниже).
-
<
>
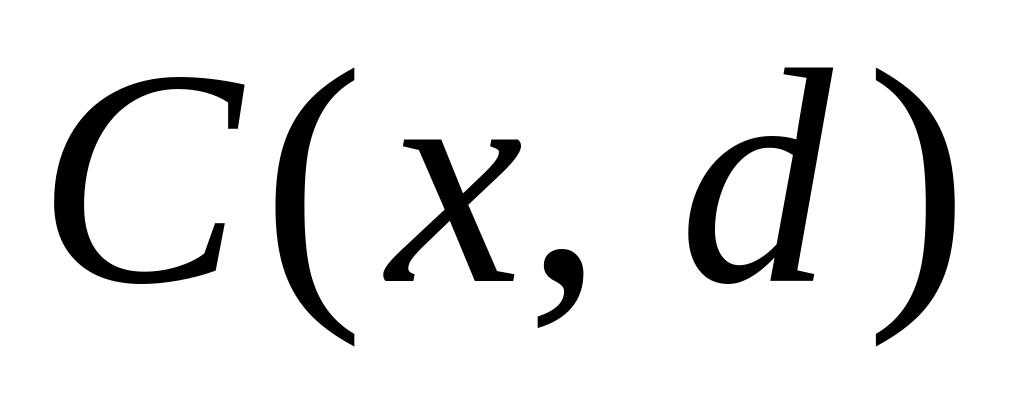
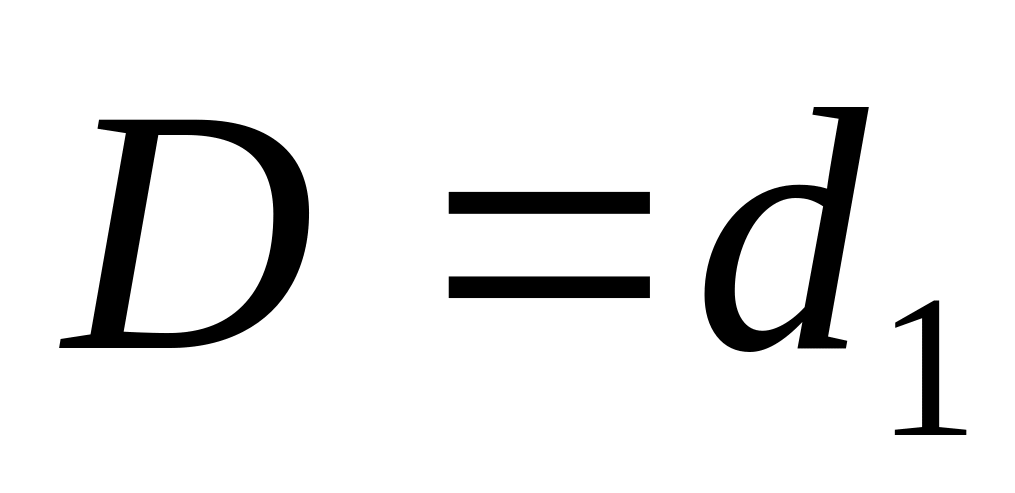
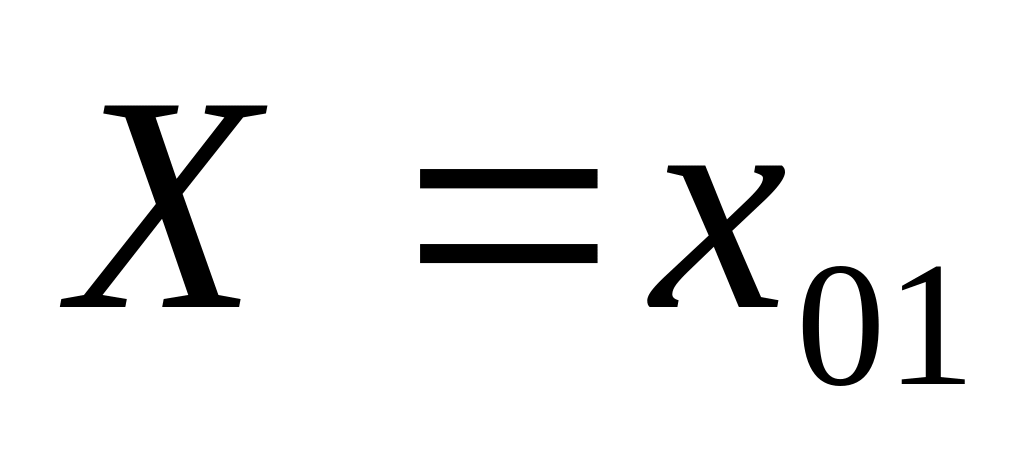
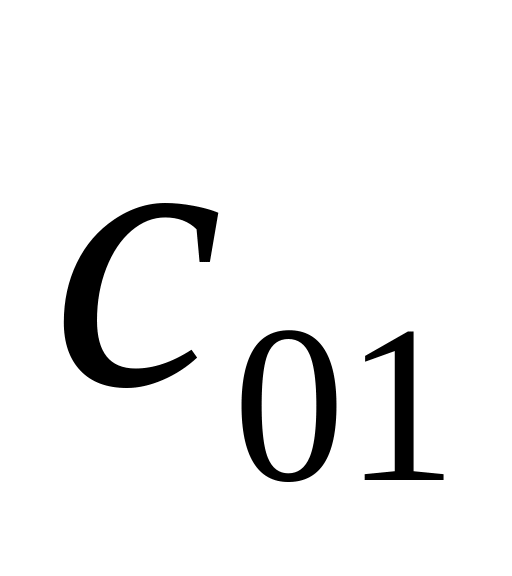
Запишем задачу в терминах доходов, т.е. определим доходы от принимаемых решений при различных состояниях природы (см. таблицу ниже).
-
>
<
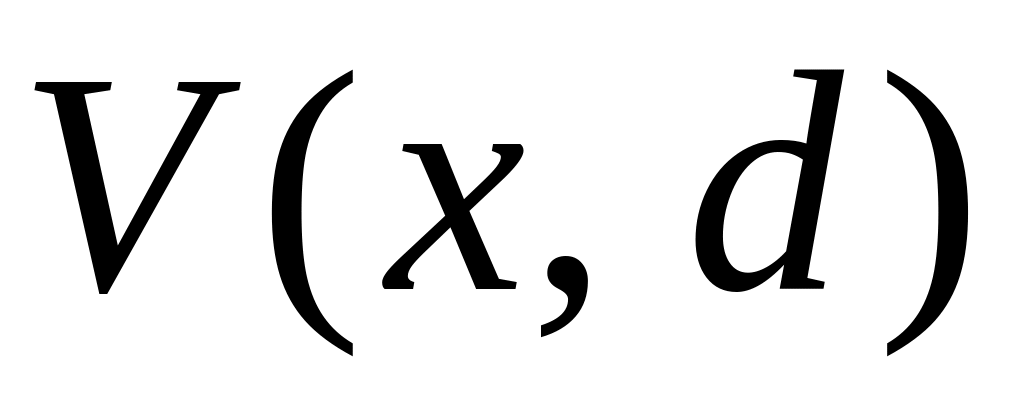
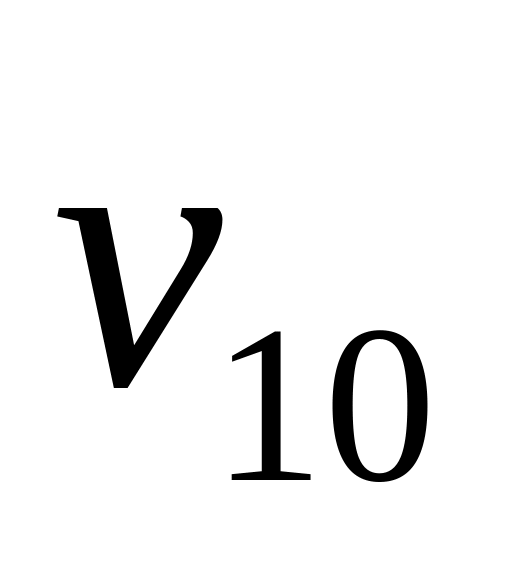
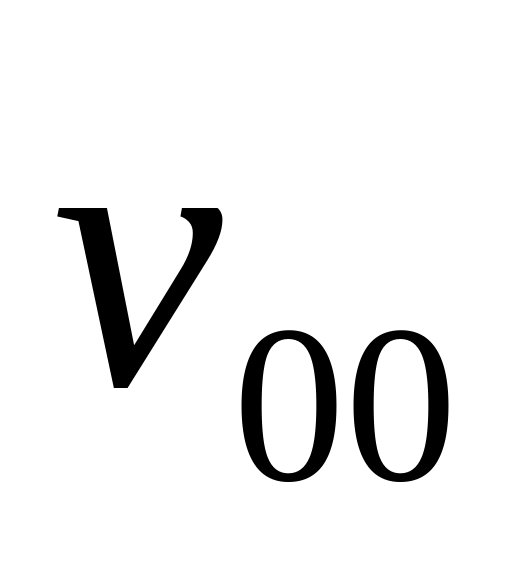
Пусть значения потерь принимают следующие значения:
= 50; = 25; = 150; = 0.
Тогда при функции дохода
значения дохода равны:
= 50; = 75; = -50; = 100.
Для принятия решения необходимо задать
функцию правдоподобия
,
или вероятность наблюдения
при состоянии природы
в случае приборных измерений
,
.
При использовании байесовского подхода
к принятию решений необходимо также
знать априорные вероятности
и
состояний окружающей среды. Априорная
вероятность заморозков
,
априорная вероятность теплой погоды
.
Пусть из многолетних наблюдений известно,
что
,
а
.
Опять же из многолетней практики
известно, что местное метеобюро правильно
предсказывает заморозки с вероятностью
,
а теплую погоду – с вероятностью
.
Тогда функция правдоподобия
принимает значения, представленные в
табл. ниже.
-
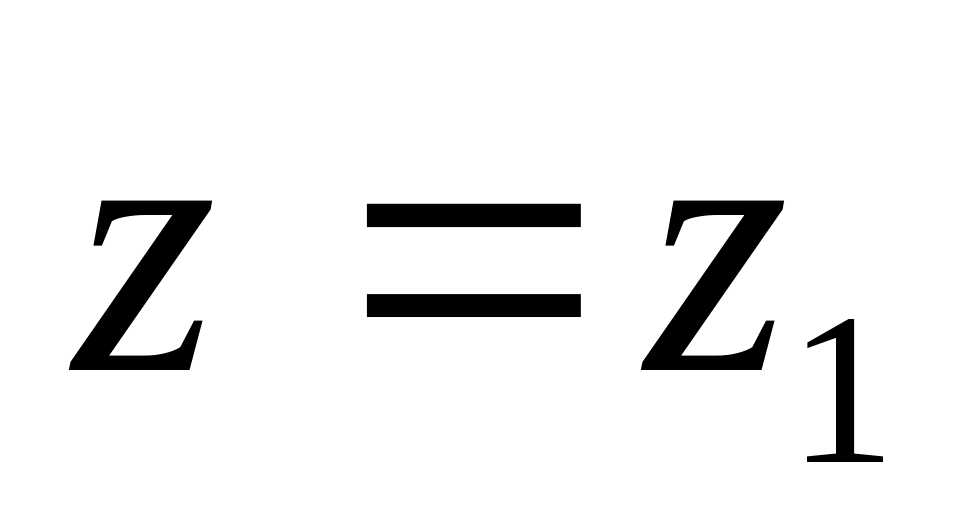
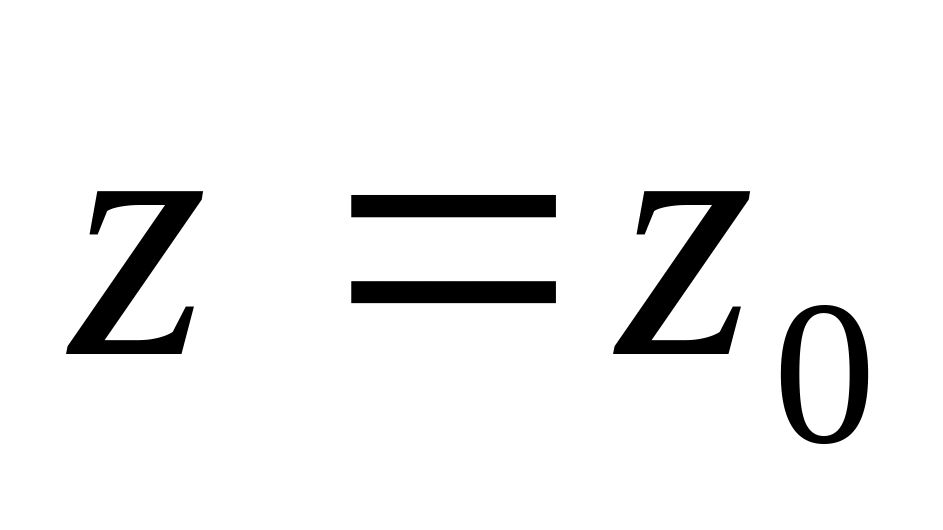
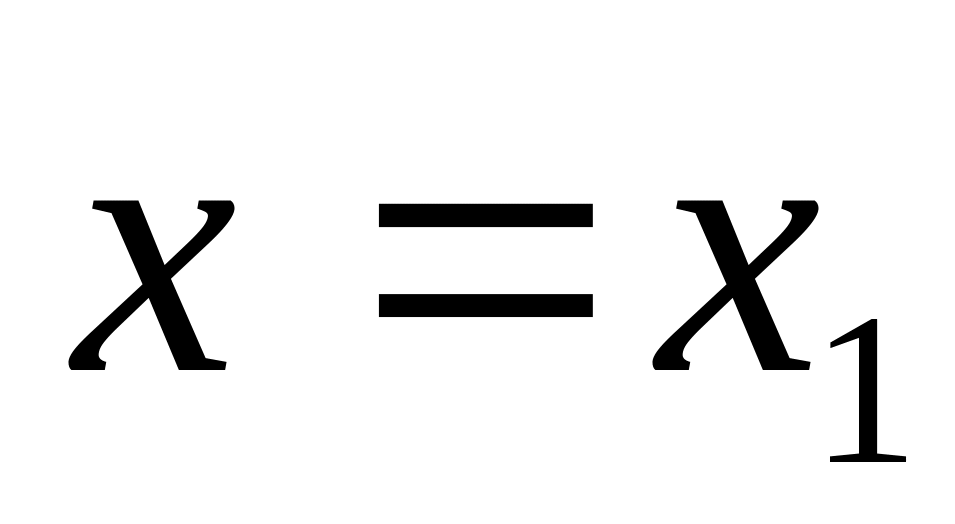
4/5
1/5
1/4
3/4
Выполним проверку корректности полученных
значений:
,
.
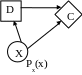
Диаграмма влияния
Диаграмма влияния представлена на рис. ниже
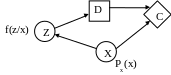
На диаграмме используются следующие
обозначения:
,
.
Данная диаграмма неудобна для построения
дерева решений, поэтому будем рассматривать
диаграмму, допускающую влияние прогноза
на состояние окружающей среды (рисунок
ниже).
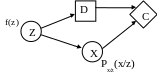
На диаграмме используются следующие
обозначения:
,
.
Выбор решения
Вычислим совместное распределение
случайных величин
и
:
в случае дискретных случайных величин
и
в случае непрерывных случайных величин.
Тогда
;
;
;
.
Представим полученные результаты в форме таблицы:
-
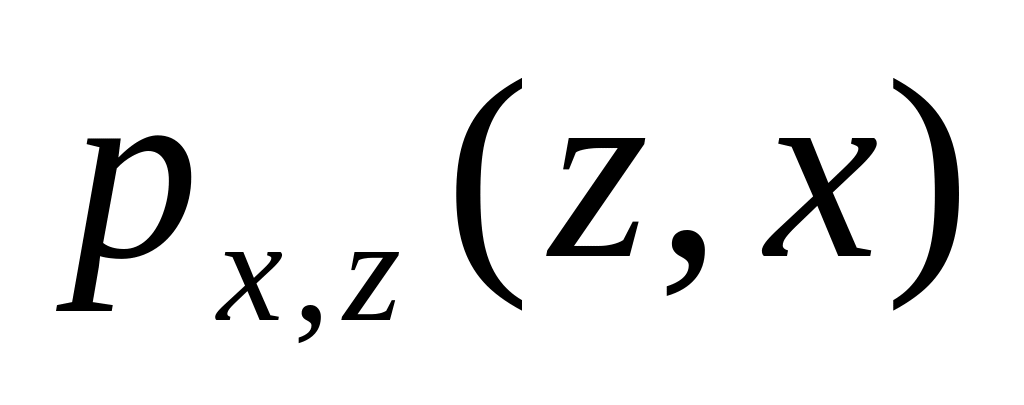
4/15
1/15
1/6
1/2
Выполним проверку корректности полученных
значений:
.
Вычислим априорное распределение
случайной величины
:
.
Тогда
;
.
Как правило, на практике априорное распределение не вычисляется.
Представим полученные результаты в форме таблицы:
-
13/30
17/30
Выполним проверку корректности полученных
значений:
.
Вычислим апостериорное распределение
,
случайной величины
по формуле Байеса:
.
Тогда
;
;
;
.
Представим полученные результаты в форме таблицы:
-
8/13
2/17
5/13
15/17
Выполним проверку корректности полученных
значений:
.
На рисунке ниже показано дерево решений:
Вычислим апостериорный риск
от принятия решения
при наблюдении
:
;
;
;
.
Так как
,
,
то байесовское решение
.
Байесовский риск
равен:
.
Осторожное решение
На рисунке ниже показано дерево решений, используемое для выбора осторожного решения.
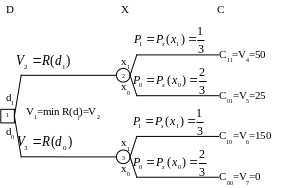
Вычислим риск от принятия решений и :
;
.
Осторожное решение
.
Риск от принятия осторожного решения
.
Вычислим цену, которую имеет смысл платить метеобюро за прогноз погоды:
,
где
– Байесово решение с прогнозом.
Откуда стоимость прогноза не должна
превышать
.
Ценность точной информации
Ценность точной информации для сторонника
осторожных решений определяется из
соотношения
,
где
– решение с точной информацией.
Диаграмма влияния при наличии точной информации имеет вид:
Дерево решений при наличии точной информации показано на рисунке ниже.
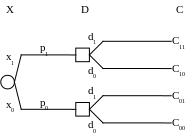
Риск от принятия решения при наличии
точной информации равен:
.
Тогда ценность точной информации для
сторонника осторожных решений
.
Для сторонника байесовских решений
ценность точной информации
,
так как точная информация полностью
устраняет риск.
Разметка дерева решений (Rollback алгоритм)
Дерево решений состоит из вершин трех
типов: “Решение”, “Случай”, “Результат
(исход)”, который выражается в терминах
потерь или дохода. Вершины типа доход
(потери) представляют собой листья
дерева. Каждая вершина независимо от
типа имеет уникальный номер
.
Из каждой вершины
могут исходить дуги, связывающие ее с
другими вершинами. Дуга определяется
парой номеров вершин
.
С каждой вершиной потерь
связана величина потерь
(дохода
).
С каждой вершиной
типа “Случай” связан набор
вершин, таких что
,
и набор
вероятностей перехода в связанную с
ней дугой вершину
:,
при этом выполняется соотношение:
.
С каждой вершиной
типа “ Решение ” связан набор
решений, таких что
,
т.е. номеров вершин, в которые можно
попасть, приняв некоторое решение.
В таблице ниже приведены множества
и
для задачи защиты посевов.
D(2)={4,5}; 
;
D(3)={6,7}; 
;
L(4)={8,9}; 
;
L(5)={10,11}; 
;
; 
.
Алгоритм разметки дерева решений
Все вершины считаются непомеченными.
1. Все вершины типа
“потери” (“доход”) пометить меткой
или
.
2. Все вершины типа
“решение”, такие, что уже помечены все
вершины
из множества
,
пометить меткой
или
.
3. Пометить вершины типа “случай”,
такие, что уже помечены все вершины
из
,
пометить меткой
.
(Риск,
связанный с потерей или полезность,
связанная с ожидаемым доходом)
4. Повторять пункты 2 и 3 пока не будет помечена корневая вершина.
В результате работы алгоритма каждая
вершина
независимо от типа помечена меткой
.
Если - вершина типа ”потери” (“доход”), тогда - потери (доход), связанные с соответствующим исходом.
Если - вершина типа “решение“, тогда - математическое ожидание потерь (дохода) при выборе наилучшего решения из и последующими наилучшими решениями.
Если - вершина типа “случай”, тогда - математическое ожидание потерь (дохода) в лотерее, соответствующей этой вершине при наилучших решениях.
Для нахождения байесова решающего правила необходимо выполнить ниже перечисленные шаги.
1. Начать с корня дерева (
).
2. В вершине
типа “решение” принимать решение,
соответствующее переходу k
q,
где
или
.
3. Из вершины
типа “случай” идти в вершину
в соответствии с наступившим событием.
4. Повторять пункты 2 и 3 пока не будет достигнута вершина типа “результат”, представляющая собой лист дерева.