Алгоритм применения байесова решающего правила .

1. Получить наблюдение .

2. Вычислить апостериорную плотность распределения случайной величины : (*)

или апостериорные характеристики состояния среды при наблюдении :

3. Вычислить апостериорный риск 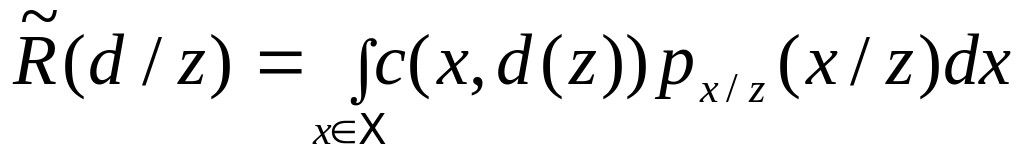для всех .

4. Выбрать решение .

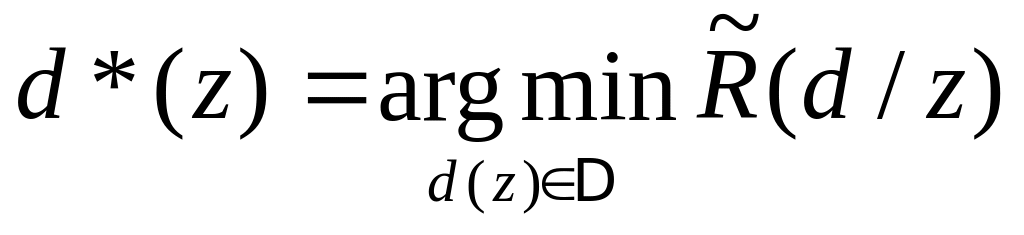Преобразуем выражение для вычисления апостериорного риска с учетом (*):

,

где .

Обозначим , тогда

, .

Максимум апостериорной вероятности

Пусть множество состояний природы , множество решающих правил Необходимо принять решение о состоянии окружающей среды.

Для решения задачи будем выдвигать гипотез о состоянии окружающей среды. Рассмотрим гипотезу о том, что среда находится в состоянии : .

Определим функцию потерь от принятия решения при состоянии среды как:

.

Тогда , или, что эквивалентно,

,

где – дельта Кронекера, .

С учетом введенных обозначений апостериорный риск равен:

.

Следовательно, необходимо принимать такое решение, которое максимизирует апостериорную вероятность нахождения окружающей среды в состоянии , при наблюдении :

.

Для вычисления апостериорной вероятности используется следующее соотношение: .

Принимается гипотеза , для которой выполняется условие: и принимается решение .

Максимум правдоподобия (МП)

Рассмотрим ситуацию, при которой неизвестны значения вероятностей , . В этом случае используется принцип недостаточного основания Бернулли.

Принцип недостаточного основания Бернулли

Принцип недостаточного основания был сформулирован Якобом Бернулли в 1713 г. В соответствии с принципом недостаточного основания все состояния природы считаются равновероятными, если нет достаточного основания считать, что одно состояние предпочтительнее другого:

.

Тогда апостериорная вероятность равна:

,

где – функция правдоподобия.

Следовательно, необходимо выбирать такое решение, которое максимизирует значение функции правдоподобия:

.

Рассмотренный метод не зависит от априорного описания среды и позволяет не рассматривать среду, как подлежащую рассмотрению аппаратом вероятности.

Пример функции правдоподобия приведен на рисунке ниже.

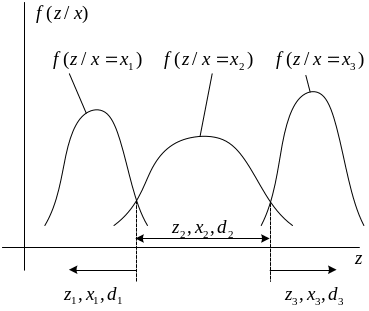
Максимальная неопределенность окружающей среды

В случае, если есть склонность к Байесовскому подходу, но не известно распределение вероятностей состояния окружающей среды, можно пытаться использовать качественную информацию о , и выбрать для принятия решения в некотором смысле наихудшее распределение, предполагая, что для того распределения, которое действительно имеет место, качество будет приемлемым.

Введем в рассмотрение функцию неопределенности . Функция неопределенности, например, энтропия, нужна, чтобы найти байесовское решающее правило, соответствующее наиболее хаотичному поведению среды. На самом деле среда менее хаотична, риски меньше, чем при принятом решающем правиле .

Задача состоит в том, чтобы вычислить набор вероятностей, соответствующих максимально возможной неопределенности:

.

Тогда байесовское решение будет определяться как:

.

Пусть , .

Вероятность выразим через все остальные вероятности:

.

Вычислим максимум :

.

Тогда ;

; , .

Следовательно, все вероятности равны между собой. Отсюда возник принцип недостаточного основания Бернулли.