Раздел II. Использование наблюдений в принятии решений
Пусть
- множество состояний природы,
- некоторое состояние,
- случайная величина описывающая
состояние природы.
- плотность распределения случайной
величины в непрерывном случае,
- функция распределения случайной
величины.
Пусть за состоянием производятся
наблюдения, результат которых выдается
в форме прогноза или измерения
.
- множество возможных значений наблюдения.
Наблюдение рассматривается как случайная
величина
,
распределение которой зависит от
состояния природы и описывается
семейством условных распределений
,
с плотностью распределения (для
непрерывного случая)
или набором вероятностей (для дискретного
случая). Все характеристики считаются
известными.
Задача заключается в построении решающего
правила
,
где
- множество возможных решений. Обозначим
как множество всех решающих правил.
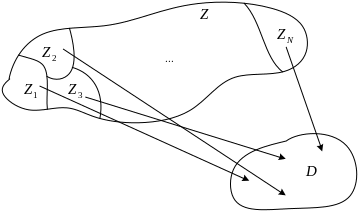
Построение решающего правила фактически
означает разбиение пространства
наблюдений
на непересекающиеся подмножества
такие, что
,
где
:
,
.
Решающие правила, риск
Определение. Риском (условным риском)
от применения решающего правила
при состоянии природы
будем называть среднее значение потерь:
,
где
- ограниченная вещественнозначная
функция потерь.
- для непрерывной случайной величины
;
- для дискретной случайной величины
.
Здесь усреднение производится по
возможным значениям наблюдений случайной
величины
при дискретном
.
Условный риск
вычисляют априори, т.е. до поступления
наблюдения
.
Отметим, что если наблюдения вообще не
производятся или не несут информации
о
,
то
и
.
По аналогии определим условную полезность:
,
где
- ограниченная вещественнозначная
функция дохода.
Байесовский и осторожный подходы к построению решающих правил
Осторожный подход к выбору решения.
При выборе осторожного решения
минимизируется максимальный риск:
,
.
или максимизируется минимальная полезность:
,
.
Байесовский подход к выбору решения.
При выборе байесовского решения
привлекается дополнительная информация
о случайной величине
,
которая выражается в виде ее распределения
на
.
Как правило, эта информация выражается
в виде плотности распределения
.
Байесовский (средний) риска от применения решающего правила равен:
.
- для непрерывной случайной величины
;
- для дискретной случайной величины
.
Полезность от применения решающего правила равна:
- для непрерывной случайной величины
;
- для дискретной случайной величины
.
При выборе байесовской решающей функции минимизируется риск:
,
.
или максимизируется полезность:
,
.
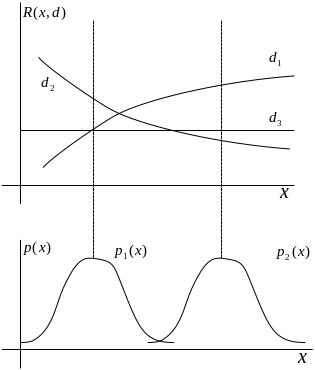
Пример. На рисунке ниже показан
пример выбора лучшего решения. При
использовании осторожного подхода
минимаксная решающая функция
.
При использовании байесовского подхода
в зависимости от значения
в качестве байесовской решающей функции
может быть выбрано
(если
дополнительная информация будет выражена
в виде
)
или
(при
если дополнительная информация будет
выражена в виде
).
