10. Сквозное уравнение напряжений нагруженного трансформатора

Это уравнение напряжений всего трансформатора в целом. Оно получается из основных уравнений при . При этом третье уравнение принимает вид

, (53)

Откуда

, (54)

, (55)

Учитывая это и тот факт, что преобразуем первое и второе уравнения

, (56)

, (57)

, (58)

, (59)

, (60)

Учитывая, что и подставляя , получаем сквозное уравнение напряжений нагруженного трансформатора

,, (61)

(*), (62)

Уравнение (*) является сквозным уравнением напряжений трансформатора. Из него

, (63)

Модуль Z_вх

, (64)

Аргумент Z_вх

, (65)

Имея , находим и

Натуральные вторичные величины:

, ., (66)

При коротком замыкании на зажимах вторичной обмотки , , . Подставив это, найдем I_1К, I_2К = КI_1К, φ_к.

11. Упрощенная схема замещения трансформатора с подключенным сопротивлением нагрузки

Из формулы тока I₁ видно, что он протекает по цепи с последовательным соединением активных и индуктивных сопротивлений. В формуле, для компактности её записи, все активные сопротивления собранны в одну группу , а индуктивные – в другую .

Чтобы схема замещения соответствовала действительности, сопротивления надо расположить парами в такой последовательности:

r₁, x₁ → r₂’,x₂’ → r’_нг, x’_нг.

r₁+jx₁ = Z₁ – сопротивление первичной обмотки трансформатора,

r₂’+jx₂’ = Z₂’ – приведенное сопротивление вторичной обмотки трансформатора,

r_нг’+jx_нг’ = Z_нг’ – приведенное сопротивление нагрузки.

Сопротивление всего трансформатора в целом при Io=0 обусловлено только сопротивлением обмоток без учета сопротивления Z_μ = r_μ + jx_μ ветви намагничивания. Таким сопротивлением трансформатор обладает в режиме короткого замыкания.

, (67)

где r_к = r₁ + r₂’ – активная составляющая Zк,

x_к = x₁ + x₂’ – реактивная составляющая Zк.

Согласно изложенному, упрощенную схему замещения трансформатора с подключенным сопротивлением нагрузки можно изображать в разных видах.

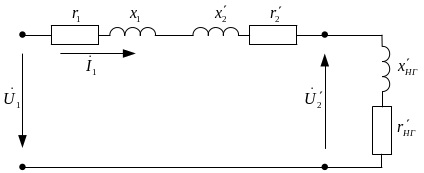
Рисунок 4

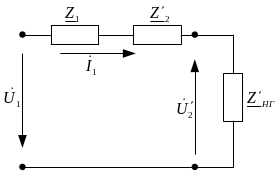
Рисунок 5

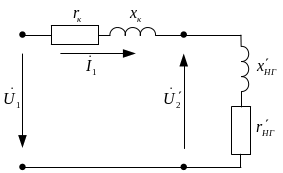
Рисунок 6

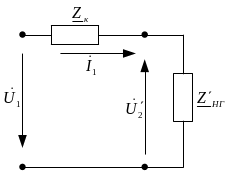
Рисунок 7

Нельзя не обратить внимание на то, что стрелка напряжения направлена встречно стрелке напряжения . Это объясняется тем, что , а . Значит .

Очень важно также заметить, что во многих инженерных расчетах не требуется знать комплексы напряжений, токов, сопротивлений, а достаточно знать только их модули. В этих случаях расчеты выполняются в действительных числах и на схеме замещения показываются действительные числа.

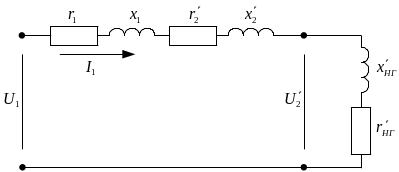
Рисунок 8

Расчет:

,, (68)

,, (69)

,, (70)

, (71)

, (72)

., (73)

Это самый простой расчет токов I₁, I₂ и напряжения U₂.

12. Вычисление величин по графику нагрузки

Дан ступенчатый график нагрузки в виде зависимости:

, (74)

и график cosφ_нг в виде такой же ступенчатой фигуры

, (75)

Требуется для каждой пары ступеней графиков вычислить:

• Полную мощность нагрузки.

• Активную мощность нагрузки.

• Реактивную мощность нагрузки.

, , , (76)

Графики и характеризуют саму нагрузку. Чтобы эту нагрузку связать с конкретным трансформатором надо:

1. Вычислить сопротивление Z_нг=r_нг+jx_нг,

2. Вычислить параметры схемы замещения для этого конкретного трансформатора,

3. Изобразить схему замещения с подключенным сопротивлением нагрузки, проставив на ней численные значения всех параметров r₁=..., x₁=..., r_m=..., x_m=..., r₂'=..., x₂'=..., r_нг'=..., x_нг'=....

4. Выполнить (по Т-образой или упрощенной схеме замещения) расчет токов I₁, I₂' и натуральной величины вторичного тока I₂=kI₂', расчет U₂' и натуральной величины вторичного напряжения U₂=U₂' / k.

Чтобы по найденным значениям U₂ и I₂ вычислить снимаемые с зажимов вторичной обмотки активную и реактивную мощности P₂ и Q₂, надо знать угол сдвига фаз φ₂ между векторами U₂ и I₂. Этот угол .

, (77)

, (78)