1.7 Построение эпюр внутренних силовых факторов

для эквивалентной системы

Найденные значения коэффициентов подставляют в систему уравнений ( 5 ) и определяют неизвестные Х₁,Х₂,…,Х_n.

Если “лишнее” неизвестное получается отрицательным, то это свидетельствует о том, что неправильно выбрано ее первоначальное направление и в эквивалентной схеме его надо изменить на противоположное.

Построение эпюр внутренних силовых факторов для эквивалентной системы ведется также как для обычной статически определимой плоской рамы.

1.8 Контроль правильности решения

Результаты расчета статически неопределимой рамы подлежат двум проверкам: статической и деформационной.

Первая заключается в проверке равновесия в узловых точках системы, т.е. в точках, где соединяются два и более стержней. Бесконечно близкими к такой узловой точке сечениями вырезается узел. Действие на него со стороны отброшенных стержней заменяется изгибающими моментами численно и по направлению совпадающими с моментами в сечениях. Равенство нулю суммы всех моментов, действующих на узел, свидетельствует о правильности результирующей эпюры изгибающих моментов.

Деформационная проверка сводится к вычислению перемещений тех сечений эквивалентной системы, которые были освобождены от “лишних” связей по направлению действия этих связей. Если система действительно эквивалентна заданной, то эти перемещения должны отсутствовать, поскольку для исходной системы они невозможны. В этом случае проверка сводится к “перемножению” каждой единичной эпюры, построенной в процессе расчета конструкции, с результирующей эпюрой изгибающих моментов.

Для повышения надежности деформационной проверки рекомендуется использовать для построения единичных эпюр иной, не использованный в расчете, но допустимый вариант основной системы.

2. Порядок расчета статически неопределимых рам методом сил

1. Определение степени статической неопределимости рамы.

2. Выбор основной системы.

3. Построение эквивалентной системы путем нагружения ос-

новной системы заданными нагрузками (P,m,q) и неизвестными усилиями, заменяющими действие отброшенных связей.

4. Запись системы канонических уравнений в форме ( 5 ).

5.Построение единичных систем путем поочередного нагружения основной системы единичными силовыми факторами по направлению действия каждой неизвестной . Определение опорных реакций и построение единичных эпюр для вспомогательных систем.

6. Нагружение основной системы заданными нагрузками, определение опорных реакций и построение “грузовой” эпюры изгибающих моментов М_хр.

7. Вычисление коэффициентов и свободных членов канонических уравнений ( 5 ) способом Верещагина с использованием формул ( 6 ).

8. Определение неизвестных путем решения системы канонических уравнений ( 5 ).

9. Определение опорных реакций в эквивалентной системе и построение эпюр продольных сил, поперечных сил и изгибающих моментов.

10. Статическая проверка равновесия узлов рамы.

11. Деформационная проверка правильности решения.

Рассмотрим конкретные примеры расчета статически неопределимых плоских рам методом сил.

П

D

р и м е р 1

q

Для системы, состоящей из стер-

жней одинаковой жесткости EI_x

В

построить эпюры внутренних

С

силовых факторов.

q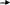

А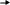

1. Для вычисления степени статической неопределимости используем формулу (1). Для заданной системы Х=4, S=3, К=0, Ш=0, следовательно n=4-3=1. Последнее означает, что рама один раз внешне статически неопределима, т.е. содержит одну связь, “лишнюю“ с точки зрения ее равновесия.

D

Х₁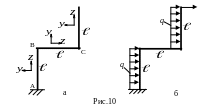

2. Принимаем за “лишнюю“ связь шарнирно-подвижную опору в т.D. Удалив эту связь и сняв заданные нагрузки получаем основную систему (рис.10а). вязь шарнирно-подвижную опору в т.Двнешне статически неопределима, т.е. 000000000000000000000000000000000000000000000000000000

3. Прикладывая к основной системе заданные нагрузки и заменяя действие отброшенной связи неизвестной силой Х₁, которая по своей сути является горизонтальной опорной реакцией в т.D, получаем эквивалентную систему (рис.10б).

4. Система канонических уравнений ( 5 ) для один раз статически неопределимой системы сводится к одному уравнению

( 9 )

Физический смысл уравнения ( 9 ) – горизонтальное перемещение сечения D от заданных нагрузок и неизвестной силы X₁ должно равняться нулю.

5

. Выбираем вспомогательную (единичную) систему (рис.11a ). Для этого к основной системе в точке D прикладываем единичную силу по направлению неизвестной силы Х₁. Определяем опорные реакции и строим единичную эпюру (рис.11б ).

D

а

б

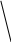
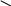
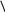
Рис. 11.

6. Грузовую систему получаем нагружая основную систему заданными внешними нагрузками (рис.12а). Определяем опорные реакции и строим “грузовую” эпюру М_хр (рис.12б).

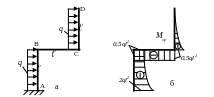
Рис. 12.

7. Вычисляем коэффициенты и уравнения ( 9 ), используя правило Верещагина. Коэффициент , суть которого – горизонтальное перемещение сечения D под действием единичной силы _, получается при умножении эпюры на саму себя. Следовательно, для каждого участка рамы, площадь под эпюрой умножается на ординату этой же эпюры, проходящей через ее центр тяжести. На участке АВ возникает необходимость в перемножении двух трапеций. Чтобы не определять центр тяжести трапеции, удобнее разбить ее на прямоугольник и треугольник, как показано на рис.13а. При этом используем следующие обозначения: кружки - центры тяжести эпюр; -площади под этими эпюрами; - ординаты, взятые со второй эпюры под центром тяжести первой.

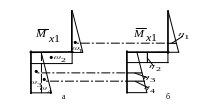
Рис.13

+ + ,

Заметим, что величина всегда положительна, т.к. площади и ординаты имеют одинаковый знак.

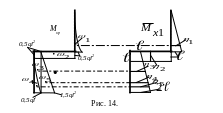Свободный член уравнения ( 9 ) вычисляем перемножая эпюры и (рис.14 ). Эпюру М_хр на участке АВ расслаиваем на три, при этом рассматриваем верхнюю отсеченную часть рамы, т.е. отбрасываем заделку в точке А.

8. Значения коэффициента и свободного члена подставляем в каноническое уравнение ( 9 ) и определяем неизвестное усилие Х₁

Так как Х₁ отрицательна, ее направление в эквивалентной системе необходимо изменить на противоположное.

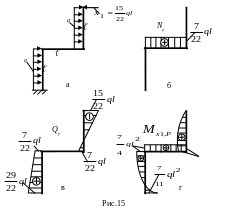
9. Раскрыв статическую неопределимость, вновь определяем в эквивалентной системе (рис.15а) опорные реакции и строим

эпюры внутренних силовых факторов (рис.15б,в,г).

10. Выполняем статическую проверку. Вырезаем узлы в точках В и С и прикладываем к ним соответствующие по величине и направлению изгибающие моменты (рис. 16).

В

С

Рис.16

Равновесие соблюдается.

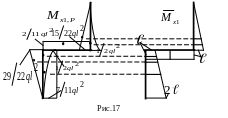
11. Выполняем деформационную проверку. Определим горизонтальное перемещение точки D энергетическим методом Мора. В качестве грузовой используем предварительно расслоенную эпюру М _х1,Р , а в качестве единичной, ранее построенную эпюру (рис.17).

Горизонтальное перемещение точки D равно нулю, следовательно задача решена верно.

П

Е

р и м е р 2

Для рамы, состоящей из стерж-

ней одинаковой изгибной жест-

кости ЕI_x=const построить эпю-

ры внутренних силовых факто-

ров.

1. Для определения степени статической неопределимости используем формулу (1). Для заданной системы Х=3, S=3, К=1, Ш=0, следовательно N=3-3+3=3. Последнее означает, что рама три раза внутренне статически неопределима, т.е. содержит одну связь, “лишнюю“ с точки зрения ее равновесия. Внешне рама статически определима.

2. Удаляем “лишние“ внутренние связи на оси симметрии

в т.Е. Удалив внутренние связи и внешнюю нагрузку получаем основную систему (рис.18а). вязь шарнирно-подвижную опору в т.Двнешне статически неопределима, т.е. 000000000000000000000000000000000000000000000000000000

Х₂

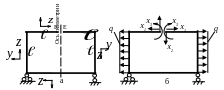
Рис. 18. 18.

3. Прикладывая к основной системе заданные нагрузки и заменяя действие отброшенных связей неизвестными силовыми факторами Х₁,Х₂,Х₃ получаем эквивалентную систему (рис.18б).

4. Система канонических уравнений ( 5 ) для три раза статически неопределимой системы сводится к системе уравнений

( 10 )

Физический смысл первого уравнения системы – взаимное горизонтальное перемещение левого и правого сечений в месте разреза под действием всех сил, включая неизвестные, равно нулю. Второе уравнение отражает аналогичное условие для взаимного вертикального перемещения сечений. В третьем уравнении отражается требование равенства нулю взаимного поворота левого сечения относительно правого в месте разреза.

5. Выбираем вспомогательные (единичные) системы. Для этого к основной системе в месте разреза прикладываем единичные силы по направлению неизвестных сил Х₁,Х₂,Х₃ соответственно. Для каждой единичной системы определяем опорные реакции и строим единичные эпюры (рис.19).

а

б

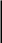
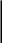
в

г

1

1

1

1

д

е

Рис. 19.

6. Грузовую систему получаем, нагружая основную систему (рис.18а) заданными внешними нагрузками (рис.20а). Определяем опорные реакции и строим “грузовую” эпюру (рис.20б).

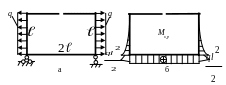
Рис. 20.

7. Коэффициенты в уравнениях системы ( 10 ) определяем, используя правило Верещагина вычисления интеграла Мора. Из четырех эпюр две являются симметричными ( ), две - -кососимметричными ( ). При перемножении симметричной эпюры на кососимметричную результат, очевидно, всегда равен нулю. Следовательно

Остальные коэффициенты соответственно равны

8. После подстановки найденных коэффициентов система уравнений (10) принимает вид

(11)

Из второго уравнения системы следует, что Х₂=0.

Решая совместно первое и третье уравнения, находим

9. Для окончательного варианта эквивалентной расчетной схемы (рис. 21а ) определяем опорные реакции и строим эпюры продольных ( N_z) и поперечных (Q_y) сил и изгибающих моментов ( ).

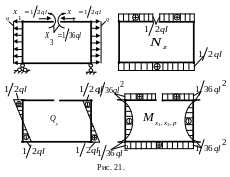
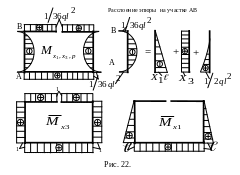
10. Выполняем деформационную проверку. Для этого перемножаем по правилу Верещагина предварительно расслоенную эпюру М_х1,х3,Р (рис.22) на единичные эпюры

Полученный результат означает, что отсутствует взаимное горизонтальное смещение и взаимный поворот смежных сечений в месте разреза, т.е. в точке Е.

П р и м е р 3

m=ql²

D

C

Для рамы, состоящей из стерж-

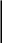
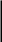
ней одинаковой изгибной жест-

кости ЕI_x=const построить эпю-

А

В

ры внутренних силовых факто-

ров.

1. Для определения степени статической неопределимости используем формулу (1). Для заданной системы Х=3, S=3, К=1, Ш=1, следовательно N=3-3+3-1=2. Последнее означает, что рама два раза внутренне статически неопределима, т.е. содержит две “лишние“ связи. Внешне рама статически определима.

2. Удаляем “лишние“ внутренние связи в точке D. Удалив внутренние связи и внешнюю нагрузку, получаем основную систему (рис.23а).

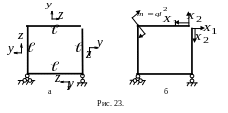
вязь шарнирно-подвижную опору в т.Двнешне статически неопределима, т.е. 0000000000000000000000000000000000000000000000000000003. Прикладывая к основной системе заданные нагрузки и заменяя действие отброшенных связей неизвестными силами Х₁,Х₂ получаем эквивалентную систему (рис.23б).

4. Система канонических уравнений ( 5 ) для дважды

статически неопределимой системы сводится к системе уравнений

(12)

Физический смысл первого уравнения системы – взаимное горизонтальное перемещение левого и правого сечений в месте разреза под действием всех сил, включая неизвестные, равно нулю. Второе уравнение отражает аналогичное условие для взаимного вертикального перемещения сечений.

5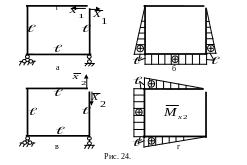 . Выбираем вспомогательные (единичные) системы. Для этого к основной системе в месте разреза прикладываем единичные силы по направлению неизвестных сил Х₁,Х₂ соответственно (рис.24а,в). Для каждой единичной системы определяем опорные реакции и строим единичные эпюры (рис.24 б,г).

6. Грузовую систему получаем, нагружая основную систему заданными внешними нагрузками (рис.25а). Определяем опорные реакции и строим “грузовую” эпюру (рис.25б).

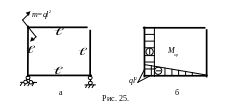
7. Коэффициенты в уравнениях системы ( 12 ) определяем, используя правило Верещагина с применением формул (6) вычисления интеграла Мора.

8. Найденные коэффициенты подставляем в канонические уравнения ( 12 ) и определяем неизвестные

9. Для окончательной эквивалентной схемы (рис.26а) определяем опорные реакции и строим эпюры внутренних силовых факторов: продольных сил N_z, поперечных сил Q_y и изгибающих моментов М_х1,х2,Р (рис.26б,в,г).

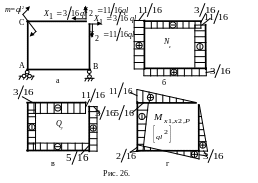
m=ql²

10. Выполняем статическую проверку. Проверяем равновесие в узловых точках А,В,С.

А

В

С

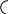
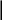
11. Выполняем деформационную проверку (рис.27).

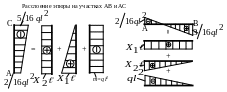
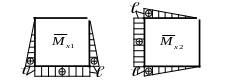
Рис. 27.

,

Полученные результаты свидетельствуют о том, что взаимные горизонтальные и вертикальные перемещения сечений в точке D отсутствуют и, следовательно, задача решена верно.