1.5. Вычисление коэффициентов и свободных членов канонических уравнений

Для определения коэффициентов и свободных членов уравнения ( 5 ) может быть использован метод Мора. Пренебрегая влиянием продольных и поперечных сил на перемещения, интеграл Мора записывают в виде

(6)

где n - степень статической неопределимости системы; - аналитические выражения изгибающих моментов, возникающих на участках основной системы только от заданных нагрузок;

- аналитические выражения изгибающих моментов, возникающих на участках основной системы только от единичных сил (моментов);

к – число участков, на которые разбита система.

При этом направления единичных сил (моментов) должны совпадать с направлениями соответствующих неизвестных.

Знак суммы в (6) указывает, что интеграл вычисляется для отдельных участков системы и результаты суммируются. Под участком понимается элемент рамы, в пределах которого хотя бы одна из эпюр изменяется по линейному закону. Таким образом кусочно-линейная эпюра должна рассматриваться, как состоящая из нескольких участков, на каждом из которых эпюра изменяется по линейному закону.

1.6. Использование свойств симметрии при раскрытии статической неопределимости

Для систем, обладающих геометрической симметрией можно сократить объем вычислений и снизить число искомых неизвестных Х₁,Х₂,…,Х_n.

Если рамная конструкция имеет ось геометрической симметрии то, как будет показано ниже, целесообразно удалить “лишние” связи (как правило, внутренние) на оси геометрической симметрии. Расчет еще более упростится, если внешняя нагрузка симметрична или обратно симметрична (кососимметрична) относительно той же оси.

Р

ассмотрим, в качестве примера, трижды статически неопределимую симметричную раму под действием кососимметричной нагрузки (рис.7а). Выбранная с учетом симметрии основная система, показана на рис.7б.

Рис. 7.

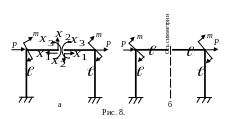В эквивалентной системе, помимо заданных внешних сил, в месте разреза возникают три неизвестных силовых фактора: симметричные Х₁, Х₃ и кососимметричный X₂ (рис. 8а).

Канонические уравнения для трижды статически неопределимой системы записываются в виде

( 7 )

Д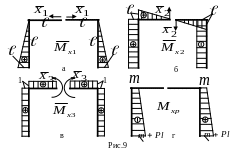 ля определения коэффициентов канонических уравнений (7) необходимо рассмотреть (создать) «грузовую» и три вспомогательных единичных системы. Для получения грузовой системы основная система нагружается только заданными нагрузками (рис.8б). Единичные системы образуются путем поочередного нагружения основной системы единичными силовыми факторами, направление которых совпадает с направлением неизвестных . Затем для каждой вновь созданной системы определяются опорные реакции и стоятся грузовая эпюра М_xp (рис.9г) и единичные эпюры . На рис.9а,б,в единичные эпюры совмещены с соответствующими расчетными схемами.

Эпюра от кососимметричного силового фактора и грузовая эпюра М_хр от заданной нагрузки являются кососимметричными, эпюры от симметричных факторов - симметричными. Нетрудно убедиться, что при перемножении симметричной эпюры на кососимметричную получается ноль и, как следствие, обращаются в ноль соответствующие перемещения (коэффициенты канонических уравнений).

Определим перемещение . Пользуясь способом Верещагина, перемножим эпюры и и получим

Аналогично, можно убедиться, что

Таким образом, система уравнений (7) упрощается и принимает вид

( 8 )

Поскольку заданные нагрузки m, P кососимметричны , то грузовая эпюра М_хр также кососимметрична и перемещения Из первого и третьего уравнений ( 8 ) следует, что симметричные усилия в месте разреза равны нулю:

Полученный результат иллюстрирует общие закономерности деформирования кососимметричных систем, а именно:

у симметричной рамы, находящейся под действием кососимметричной нагрузки, в сечении на оси симметрии заведомо равны нулю симметричные лишние неизвестные.

Аналогичным образом можно показать, что у геометрически симметричной рамы с симметричной нагрузкой, в сечении на оси симметрии равны нулю кососимметричные лишние неизвестные.