1.2. Выбор основной системы

Основной называется статически определимая и геометрически неизменяемая система, полученная из исходной путем удаления заданных нагрузок и отбрасывания “лишних” связей. Поскольку в качестве “лишних” могут рассматриваться различные комбинации из фактических связей, то основная система может выбираться различными способами.

На раму, изображенную на рис.4а, наложено четыре связи: двухсвязная (шарнирно-неподвижная) опора А и две односвязные (шарнирно-подвижные) опоры В и С.

В

В

А

А

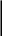
q

С

С

а

б

Рис.4

Система имеет одну лишнюю связь. Поскольку основная система должна быть геометрически неизменяема, заключаем, что нельзя отбросить ни горизонтальную, ни вертикальную связи в точке А. В первом случае основная система получила бы возможность двигаться в горизонтальном направлении, а во втором – вращаться вокруг точки В, где пересекаются линии действия реакций всех оставшихся связей. Можно отбросить либо опору В, либо опору С. Второй вариант показан на рис.4б.

Рама, показанная на рис.5а, внешне статически определима, но содержит замкнутый контур, который внутренне дважды статически неопределим.

C

C

Р

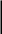
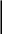
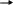
Рис. 5.

а б

Один из возможных вариантов основной системы представлен на рис.5б. Удаление шарнира в точке С разрешает взаимный поворот смежных сечений.

1.3. Выбор эквивалентной системы

Основная система под действием только заданных нагрузок деформируется не так как исходная. Это происходит потому, что после устранения “лишних” связей сечения, на которые они были наложены, получают возможность смещаться по тем направлениям, по которым это было запрещено в исходной системе.

Чтобы этого избежать, необходимо сохранить силовое воздействие на основную систему со стороны отброшенных связей. Для этого заданные внешние нагрузки дополняются неизвестными силовыми факторами Х₁,Х₂,…,Х_n соответствующими характеру убранного ограничения на перемещения и приложенными в местах отброшенных лишних связей. Снятое ограничение на линейное перемещение заменяется неизвестной силой, на угловое перемещение – моментом. Если удаленная связь ограничивала горизонтальное перемещение сечения- неизвестная сила должна быть горизонтальной, если вертикальное – вертикальной. Направление при этом значения не имеет.

Таким образом, приложив к основной системе заданные нагрузки и неизвестные силовые факторы, получают эквивалентную систему. Она будет деформироваться как заданная и следовательно, внутренние усилия, возникающие в исходной и эквивалентной системах будут совпадать между собой. При этом предполагается, что неизвестные Х₁,Х₂,…,Х_n должны быть такими, чтобы перемещения сечений по направлению отброшенных связей были такими же как в исходной системе т.е. равными нулю.

Например, для рам, показанных на рис.4а,5а, выбрав в качестве основных системы, представленные на рис.4б,5б, получим соответственно эквивалентные системы, изображенные на рис. 6а,6б.

Р

Х₁

Х₂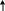

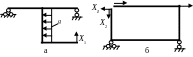
Рис. 6.