
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №12
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №14
- •Вопрос 1
- •Вопрос 3
- •Вопрос 1
- •Вопрос 3
- •Билет №16
- •Вопрос 1
- •Вопрос 3
Билет 1
Вопрос 1
Функция — математическое понятие, отражающее связь между элементами множеств. Более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Область определения функции — множество, на котором задаётся функция
Вопрос 3
Определение. Предел
от суммы 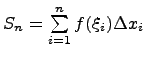 при
при ![]() ,
если он существует и конечен,
называется определенным
интегралом от
функции
,
если он существует и конечен,
называется определенным
интегралом от
функции ![]() в
пределах от
в
пределах от ![]() до
до ![]() и
обозначается:
и
обозначается:
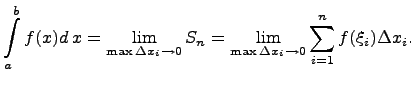
Если
существует определенный
интеграл от
функции
,
то в этом случае функция называется интегрируемой
на отрезке ![]() .
.
Билет 2
Вопрос 1
Четность функции определяется правилом f(-x)=f(x), нечетность функции определяется f(-x)=-f(x)
Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). То есть должна обладать св-ом f(x+T)=f(x), где Т – период функции.
Функция называется ограниченной, если существует такое положительное число M, что
|f ( x )| ≤M для всех значений x .
Вопрос 3
1)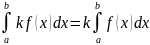 где
k
- константа
где
k
- константа
2)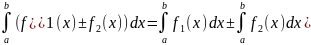
3)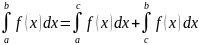 где с
где с
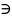 (a;b)
– значение аргумента х, делящее отрезок
(a;b)
на две части
(a;b)
– значение аргумента х, делящее отрезок
(a;b)
на две части
Билет 3
Вопрос 1
Производной функцией y=f(x)называется предел отношений приращения функции к приращению его к аргументу при стремлении к нулю последнего. Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
Вопрос 3
Формула Ньютона-Лейбница. Методы вычисления определенного интеграла
Если
F(x) — первообразная для![]() (х),
то
(х),
то
![]()
Эта формула называется формулой Ньютона—Лейбница
Формула
интегрирования по частям для определённого
интеграла. Если u(x), v(x) -
непрерывно дифференцируемые функции,
то  .
.
![]() Док-во.
Интегрируем равенство
Док-во.
Интегрируем равенство ![]() в
пределах от a до b:
в
пределах от a до b: 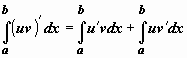 .
Функция в левом интеграле имеет
первообразную uv, по формуле
Ньютона-Лейбница
.
Функция в левом интеграле имеет
первообразную uv, по формуле
Ньютона-Лейбница 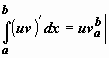 ,
следовательно,
,
следовательно, 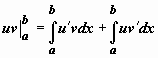 ,
откуда и следует доказываемое
равенство.
Пример:
,
откуда и следует доказываемое
равенство.
Пример: 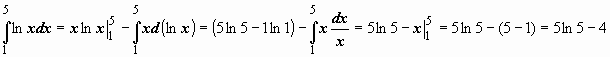 Замена
переменной в определённом интеграле.
Замена
переменной в определённом интеграле.
Теорема.
Пусть функция ![]()
определена, непрерывно дифференцируема и монотонна на отрезке
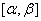 ,
,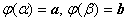 ,
,функция
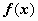 непрерывна
на отрезке [a, b].
непрерывна
на отрезке [a, b].
Тогда 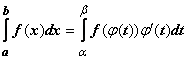 .
.
Док-во.
Пусть F(x) - первообразная для
функции f(x), т.е. ![]() ,
тогда
,
тогда ![]() -
первообразная для функции
-
первообразная для функции ![]() .
. 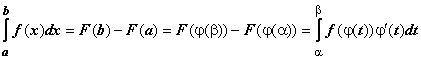 ,
что и требовалось доказать.
,
что и требовалось доказать.
Билет 4
Вопрос 1
Если
функция ![]() имеет
конечную производную в точке x0, то
в окрестности U(x0) её
можно приблизить линейной
функцией
имеет
конечную производную в точке x0, то
в окрестности U(x0) её
можно приблизить линейной
функцией
![]()
Функция fl называется
касательной к f в
точке x0. Число ![]() является
угловым коэффициентом
или тангенсом угла наклона касательной
прямой
является
угловым коэффициентом
или тангенсом угла наклона касательной
прямой
