2.5. Подбор квадратного, прямоугольного, круглого и кольцевого сечений

Итак, в разделе 2.3 из условия прочности мы получили необходимую величину момента сопротивления сечения .

Для прямоугольного сечения, у которого h = 1,5b, момент сопротивления изгибу равен W_x = bh²/6 = b(1,5b)²/6 = 400.

Отсюда находим = 10,22 см, h = 1,5b = 15,33 см.

Площадь прямоугольного сечения равна А_пр = bh = 156,7 см².

В случае квадратного сечения, у которого h = b = а, момент сопротивления изгибу равен W_x = аа²/6 = а³/6 = 400.

Отсюда находим = 13,39 см.

Площадь квадратного сечения равна А_кв = а² = 179,3 см².

Для кольцевого сечения, у которого D = 1,5d, момент сопротивления изгибу равен

W_x = (/32)D³[1-(d/D)⁴] = (/32)D³[1-(1/1,5)⁴] = 400.

Отсюда находим = 17,19 см, d = D/1,5 = 11,46 см.

Площадь кольцевого сечения равна

А_тр = (/4)D²[1-(d/D)²] = (/4)17,19²[1-(1/1,5)²] = 128,9 см².

Для сплошного круглого сечения момент сопротивления равен W_x = (/32)D³ = 400.

Отсюда находим = 15,97 см.

Площадь круглого сечения равна

А_кр = (/4)D²= (/4)15,97² = 200,4 см².

Так как объем материала, который необходимо затратить на изготовление балки, прямо пропорционален площади ее поперечного сечения, то и масса балки оказывается пропорциональной площади поперечного сечения. Поэтому относительную массу балки при разных вариантах поперечного сечения можно оценить по отношению площадей поперечных сечений, рассчитанных по условию равной прочности. Сравнение площадей поперечных сечений разной формы, с площадью равнопрочного двутавра, проведено в таблице.

Форма сечения	Круг	Квадрат	Прямоугольник	Кольцо	Двутавр
Площадь сечения А, см2	200,4	179,3	156,7	128,9	46,5
Отношение площадей ААдв	4,31	3,86	3,37	2,77	1

Как видим, рассчитываемая балка будет иметь наименьшую массу, если ее изготовить из двутаврового профиля. Балка, имеющая сплошное круглое поперечное сечение, будет самой массивной из рассмотренных пяти вариантов. Она оказалась в 4,31 раза тяжелее, чем двутавровая. Двутавровое сечение наиболее рационально при изгибе.

3. Расчет рамы

Для рамы, нагруженной сосредоточенным моментом 20 кНм, сосредоточенной силой 32 кН и погонной нагрузкой 8кНм (рис.7), требуется:

1) определить реакции опор и сделать проверку;

2) построить эпюры внутренних силовых факторов;

3) из расчета на прочность по максимальным нормальным напряжениям подобрать номер двутаврового профиля, из которого следует изготовить раму, приняв допускаемое напряжение (или расчетное сопротивление );

4) с помощью интегралов Мора найти вертикальное и горизонтальное перемещение сечения А и угол поворота сечения В, приняв модуль упругости .

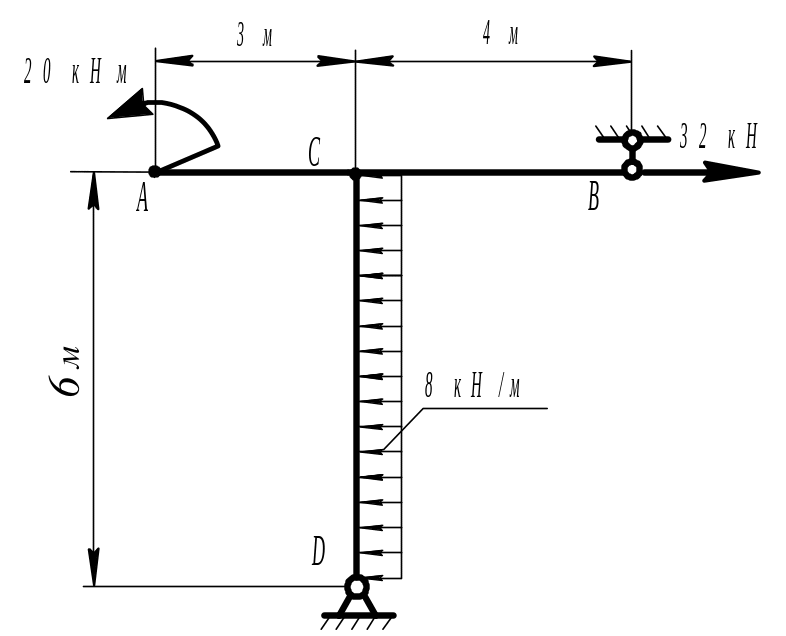
Рис.7. Расчетная схема рамы

3.1. Определение реакций опор

Найдем реакции H_D, V_D и V_B (рис.8) из уравнений равновесия рамы.

,

,

.

Сделаем проверку, вычислив сумму моментов относительно произвольной точки, например, относительно точки С:

.

С ледовательно, реакции опор найдены правильно.

Рис.8. К определению реакций опор Рис.9. К расчету N, M, Q