§ 3.6. Приведение матрицы к жордановой нормальной форме.

В предыдущем параграфе мы выяснили, что если матрица с элементами из поля приводится к жордановой нормальной форме, то эта форма определяется для матрицы однозначно с точностью до расположения жордановых клеток на главной диагонали. В этом параграфе мы укажем условие того, чтобы матрица допускала такое приведение, а так же способ практического разыскания жордановой матрицы, подобной матрице , если такая жорданова матрица существует.

ТЕОРЕМА 1. Матрица с элементами из поля тогда и только тогда приводится в поле к жордановой нормальной форме, если все характеристические корни матрицы лежат в самом основном поле .

В самом деле, если матрица подобна жордановой матрице , то эти две матрицы обладают одними и теми же характеристическими корнями. Характеристические корни матрицы находятся, однако, без всяких затруднений: так как определитель матрицы равен произведению ее элементов, стоящих на главной диагонали, то многочлен разлагается над полем на линейные множители и его корнями служат числа, стоящие на главной диагонали матрицы , и только они.

Обратно, пусть все характеристические корни матрицы лежат в самом поле . Если отличные от инвариантные множители матрицы будут

, (10)

то

.

Действительно, определители матрицы и ее канонической матрицы могут отличаться друг от друга лишь постоянным множителем, который на самом деле равен , так как именно таков старший коэффициент характеристического многочлена . Таким образом, среди многочленов (10) нет равных нулю, сумма степеней этих многочленов равна и все они разлагаются над полем на линейные множители последнее ввиду того, что, по условию, многочлен обладает таким разложением.

Пусть (8) будут разложения многочленов (10) в произведения степеней линейных множителей. Назовем элементарными делителями многочлена , отличные от единицы степени различных линейных двучленов, входящие в его разложение (8), т. е.

Элементарные делители всех многочленов (10) назовем элементарными делителями матрицы и выпишем их в виде таблицы (7).

Возьмем теперь жорданову матрицу порядка , составленную из жордановых клеток, определяемых следующим образом: каждому элементарному делителю матрицы ставим в соответствие жорданову клетку порядка , относящуюся к числу . Очевидно, что отличными от инвариантными множителями матрицы будут многочлены (10) и только они. Поэтому матрицы и эквивалентны и, следовательно, матрица подобна жордановой матрице . □

Пример 5. Найти жорданову нормальную форму матрицы

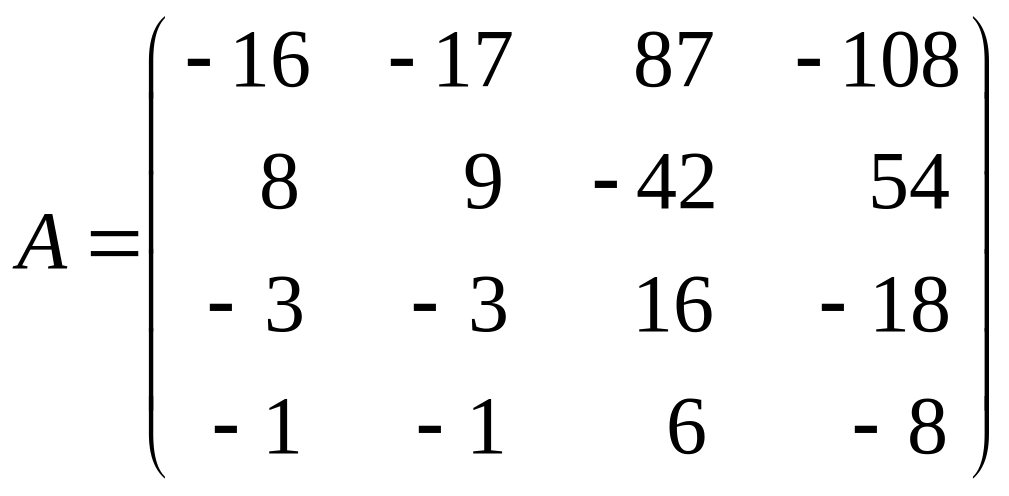
Решение. Приводя обычным способом матрицу к каноническому виду, получим, что отличными от единицы инвариантными множителями этой матрицы будут многочлены

Мы видим, что матрица приводится к жордановой нормальной форме далее в поле рациональных чисел. Ее элементарными делителями являются многочлены и , а поэтому жордановой нормальной формой матрицы служит матрица

.

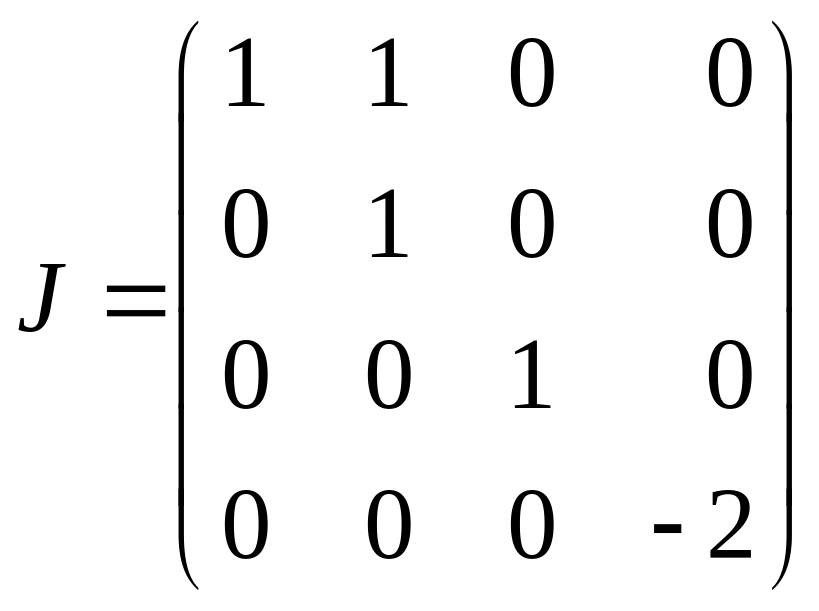На основании предшествующих результатов может быть доказано, наконец, следующее необходимое и достаточное условие приводимости матрицы к диагональному виду.

ТЕОРЕМА 2. Матрица порядка с элементами из поля тогда и только тогда приводится к диагональному виду, если все корни последнего инвариантного множителя ее характеристической матрицы лежат в поле , причем среди этих корней нет кратных.

ДОКАЗАТЕЛЬСТВО. В самом деле, приводимость матрицы к диагональному виду равносильна приводимости к такому жорданову виду, все жордановы клетки которого имеют порядок . Иными словами, все элементарные делители матрицы должны быть многочленами первой степени. Так как, однако, все инвариантные множители матрицы являются делителями многочлена , то последнее условие равносильно тому, что все элементарные делители многочлена имеют степень , что и требовалось доказать. □