Глава 3.

ЛИНЕЙНЫЕ ОПЕРАТОРЫ.

§3.1. Матрицы линейных операторов.

Пусть дано множество ; его элементы будут обозначаться малыми латинскими буквами: Пусть, далее, в множестве определены операция сложения, ставящая в соответствие всякой паре элементов из однозначно определенный элемент из , называемый их суммой, и операция умножения на действительное число, причем произведение элемента на число , однозначно определено и принадлежит к .

Элементы множества будут называться векторами, а само действительным линейным (или векторным, или аффинным) пространством, если указанные операции обладают свойствами из §2.1. Так, арифметическое мерное векторное пространство является примером линейного пространства.

Два линейных пространства и называются изоморфными, если существует биективное отображение , ставящее в соответствие каждому вектору пространства вектор пространства , такое что:

Пусть базис и . Так как система порождающих, то найдутся числа такие, что . Если также , то имеем . Но линейно независимая система, откуда . Значит . Итак, представление вектора в виде линейной комбинации базисных векторов возможно и единственно. Набор ( ) называется координатами вектора х в базисе .

Отображение называется линейным оператором, если выполнены условия: для всех и числа :

(а)

(б) ,

которые можно заменить одним: для всех и чисел верно . Отсюда следует равенство

,

широко используемое в дальнейшем.

Справедлива следующая

ТЕОРЕМА (о существовании и единственности ). Пусть базис и произвольные векторы из . Тогда существует единственный линейный оператор такой, что .

ДОКАЗАТЕЛЬСТВО. Если , то зададим так: . Проверим, что линейный оператор. Если и произвольные числа, то

Предположим, что также линейный оператор , причем .

Имеем . Итак для любого . Значит . □

Доказанная теорема показывает, что линейный оператор однозначно определяется в данном базисе своими значениями . Приходим к определению: матрицей линейного оператора в базисе называется такая матрица , у которой столбец есть координаты вектора в базисе . Т. е.,

.

Обозначим через столбец из координат вектора в базисе , т.е. . В частности, столбец из координат вектора в этом же базисе.

Имеет место следующее равенство

(1)

Действительно,

Но в последней сумме коэффициенты при как раз есть координаты вектора в базисе . Из правила умножения матрицы на столбец получаем искомое равенство (1). □

Пусть другой базис L. Матрицей перехода от одного базиса к другому называется такая матрица , у которой i-ый столбец есть координаты вектора в базисе , т. е.

Фактически матрица есть матрица линейного оператора, переводящего векторы в .

Пусть 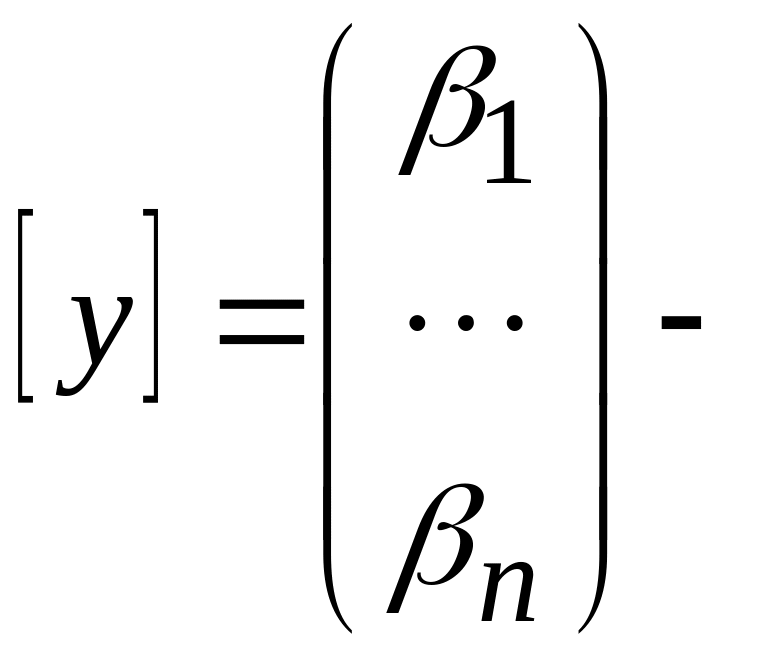столбец из координат вектора х в базисе Тогда имеет место следующее равенство

(2)

Действительно, имеем

Но откуда

Но в последней сумме коэффициенты при как раз и есть координаты вектора х в базисе . Из правила умножения матрицы на столбец получаем (2).

По следствию 2 из теоремы о ранге матриц невырожденная матрица, т.к. её столбцы, будучи координатами базисных векторов линейно независимы. Поэтому Т имеет обратную матрицу . Умножая обе части равенства (2) слева на , получаем

Пример 1.

Векторы заданы своими координатами в некотором базисе . Показать, что векторы сами образуют базис, и найти координаты вектора x в этом базисе.

Решение. Составим матрицу перехода от базиса к системе векторов :

,

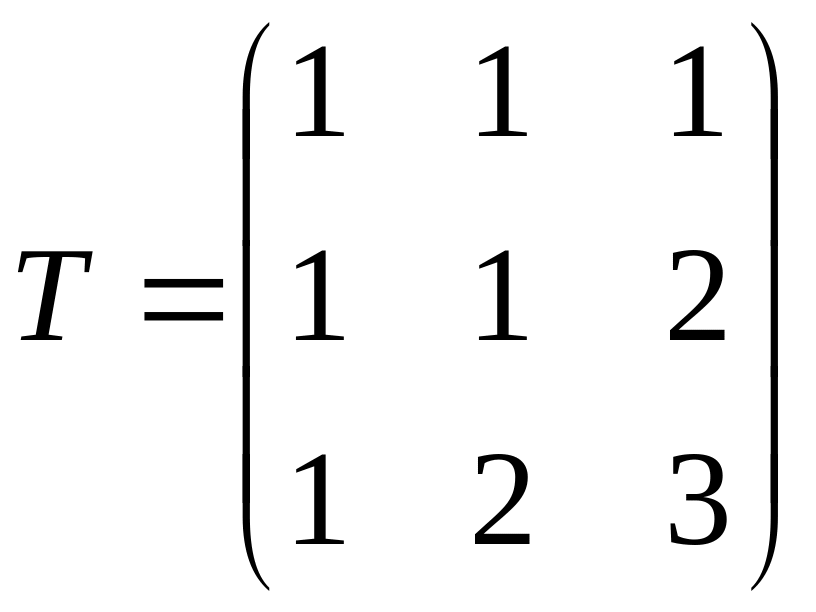она невырожденная, значит векторы линейно независимы и могут образовывать базис трёхмерного пространства. Тогда

Найдём координаты вектора в базисе

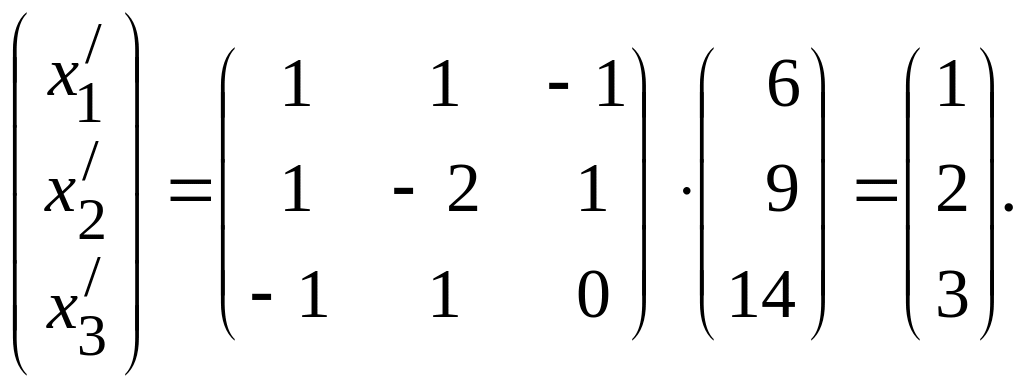
Следующая теорема устанавливает связь между матрицами одного и того же линейного оператора, заданными в разных базисах.

ТЕОРЕМА (о связи матриц линейного оператора). Пусть и – матрицы линейного оператора в базисах и соответственно и матрица перехода о первого базиса ко второму. Тогда (матрицы и называются подобными).

ДОКАЗАТЕЛЬСТВО. Если , то обозначим через и столбцы из координат вектора в первом и во втором базисах, а через и координаты образа этого вектора в первом и во втором базисах.. Из равенства (2) имеем

Из равенства (1) получаем

и .

Из этих трех равенств заключаем, что

.

Но откуда

.

Домножая обе части этого равенства на слева, получаем равенство

Которое имеет место при любом векторе . Это означает равенство матриц и . □

В доказательстве теоремы молчаливо использовался тот факт, что если для любого вектора х выполнено , то . Предлагается его доказать читателю.

Пример 2. Линейный оператор в базисе имеет матрицу 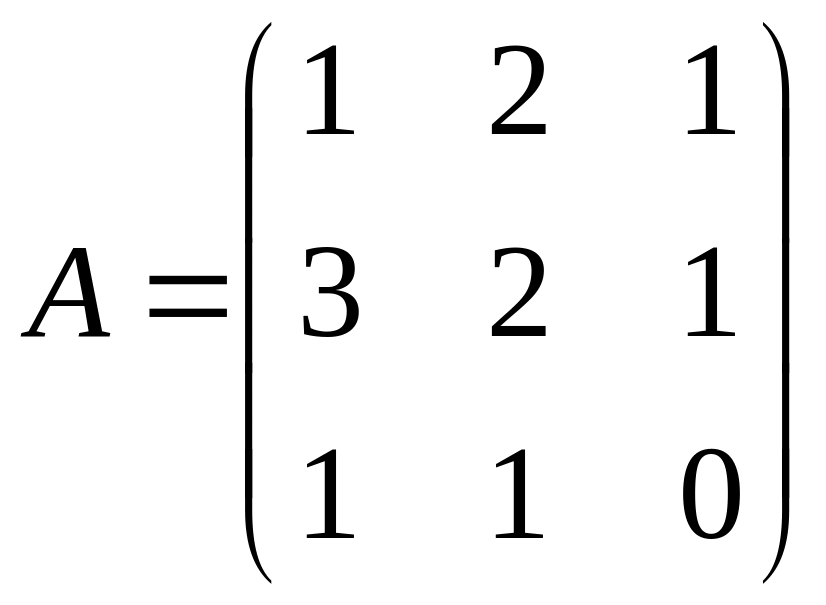. Найти его матрицу в базисе

Решение. Составим матрицу перехода от базиса к базису :

Найдём обратную матрицу для :

.

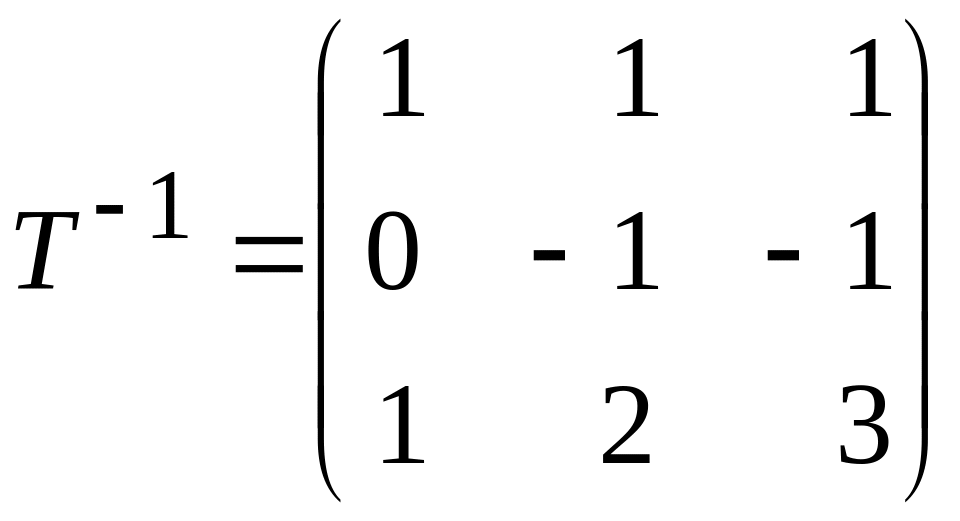Тогда