1.Электрический расчет заданной цепи при гармоническом входном воздействии.
В соответствии с заданием электрический расчет состоит из двух этапов - определение вида и параметров характеристического сопротивления нагрузки и затем расчет цепи с найденной нагрузкой.
Для дальнейшего расчета понадобятся значения следующих величин:
-5-
.
1.1. Определение вида и параметров характеристического сопротивления нагрузки.
В соответствии с заданием нагрузкой цепи должно являться его характеристическое сопротивление:
(1)
В
соответствии с теорией четырехполюсников
[Л1] характеристическое сопротивление
может быть определенно через параметры
холосто хода и короткого замыкания по
следующей формуле:
(2)
Исходя
из (2) видно, что для определения
достаточно определить только два
параметра -
и
.
Сопротивление
это сопротивление между выводами
схемы при разомкнутых выводах
(рис.2).
Рис. 2. Схема для определения
Из рис.2 видно, что определяется по формуле:
Представляем численные значения в эту формулу и, после очевидных преобразований, находим:
(3)
Сопротивление
это сопротивление между выводами
при коротком замыкании между выводами
.
Эта схема представлена на рис.3.
-6-
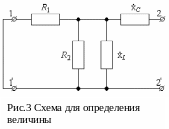
Из схемы рис.3 видно, что определяется по формуле:
После подстановки в эту формулу численных значений и очевидных преобразований, находим:
(4)
При
вычислениях рекомендуется уменьшать
численные значения выражений путем их
взаимного сокращения. Так при вычислении
дроби в
целесообразно сделать сокращение
числителя и знаменателя на
.
Найденные значения и подставляем в формулу (2):
.
Исходя из (1), запишем:
(5)
Из (5) получаем:
(6).
Реактивная
(мнимая) составляющая
может быть или индуктивностью или
конденсатором. Как известно, индуктивное
сопротивление имеет положительное
-7-
значение, а емкостное сопротивление имеет отрицательное значение. Наличие минуса в реактивной составляющей сопротивления говорит о том, что реактивной
составляющей
согласованной нагрузки является
конденсатор. Обозначим реактивную
составляющую сопротивления через
.
Найдем величину конденсатора нагрузки.
.
Из последнего соотношения находим.
.
Итак, согласованная нагрузка представляет цепь из последовательно соединённых резистора и конденсатора (рис.4).
Рис.4. Схема согласованной нагрузки.
Элементы цепи нагрузки имеют следующие значения:
,
,
.