Исходные данные:
В канале трапециидального поперечного сечения сооружается бетонная плотина с водосливом практического профиля(рисунок 1).
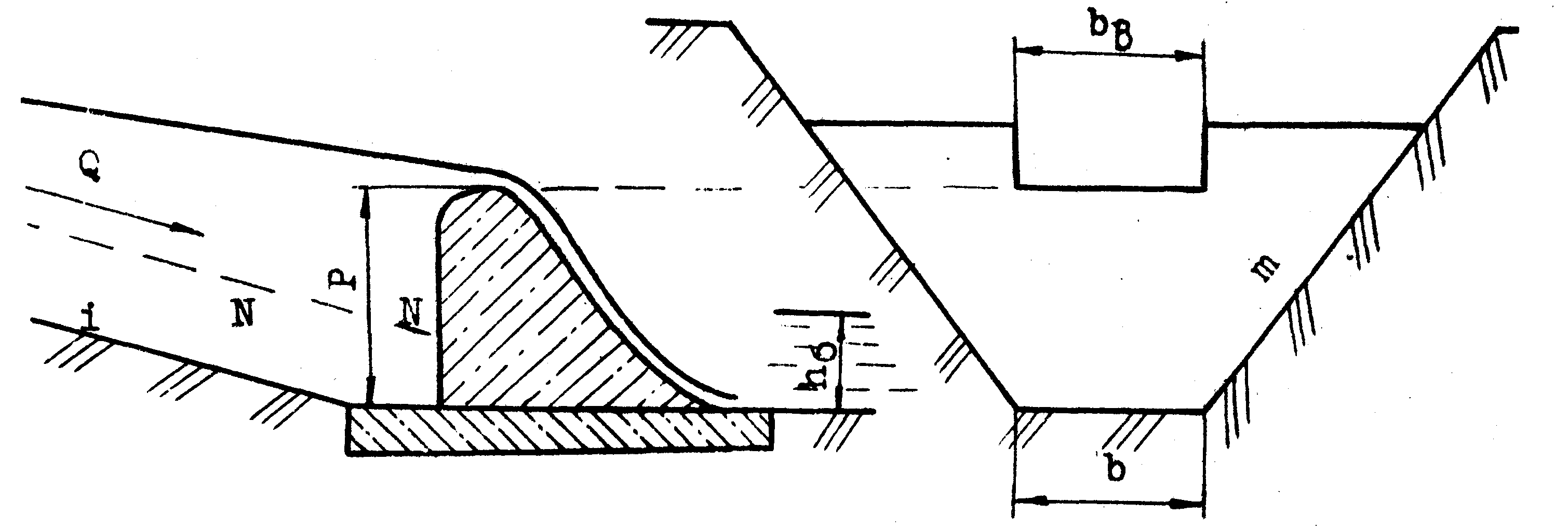
Рисунок 1 – Расчетная схема неравномерного движения воды через плотину
Таблица 1-Исходные данные.
Вариант |
Параметры |
|||||
|
|
|
|
|
|
|
29 B |
31.8 |
8 |
0.00056 |
1.81 |
1.37 |
0.02 |
- расчетный расход, м³/с;
- ширина канала по дну, м;
- продольный уклон дна канала;
- высота водослива и высота стенки перепада, м;
- бытовая глубина, м;
- нормальная глина.
1 Построение кривой свободной поверхности потока.
1.1 Определение нормальной глубины наполнения.
Глубину наполнения канала
определяем методом подбора.
Находим модуль расхода
,
который характеризует расчитываемый
канал
,
(1)
где - расчетный расход воды, м3/с;
- продольный уклон дна канала.
Следовательно,
.
Составляем таблицу 2,
в которой задаемся рядом значений
(
=1;2;3;4м)
и для каждого
определяем
соответствующий модуль расхода
.
Таблица 2 – Расчет модуля расхода.
|
|
|
|
|
|
1 |
10 |
12,47 |
0,80 |
47,82 |
427,71 |
2 |
24 |
16,94 |
1,42 |
53,63 |
1533,78 |
3 |
42 |
21,42 |
1,96 |
57,20 |
3363,36 |
4 |
64 |
25,89 |
2,47 |
59,91 |
6025,98 |
1,86 |
21,8 |
16,32 |
1,33 |
52,93 |
1330,71 |
Площадь поперечного сечения для данного русла определяется по формуле
,
(2)
где - ширина канала по дну, м;
- коэффициент заложения откоса,
принимаем
[1, с. 85].
Следовательно,
.
Длина смоченного периметра X определяем по формуле
,
м (3)
Следовательно,
.
Гидравлический
радиус
определяем по
формуле
,
м (4)
Следовательно,
.
Коэффициент Шези определяем по формуле
,
(5)
где
- коэффициент
шароховатости русла, принимаем
[1, с.86];
- коэффициент зависищий
от шароховатости и гидравлического
радиуса русла
[1] .
Следовательно,
Модуль расхода водослива
,
(6)
Следовательно,
.
По данным таблицы
2 строим график зависимости
.
По графику определяем .
Из графика зависимости
находим, что
равно 1,86м.
Для контроля правильности определения нормальной глубины необходимо подставить найденное значение в формулу модуля расхода, в результате должно получиться значение , причем расхождение не должно быть более 2%.
,
(7)
Следовательно,
