4. Проверка гипотезы по критерию х2.

Продолжаем таблицу 2. В восьмой столбце, используя данные пятого столбца и найденное значение S,запишем . В девятом столбце поместим значения f (z_i), найденные по таблице нормированной плотности

f(x)= .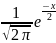

В десятом столбце запишем

np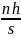_i = f (z_i).

Для этого заранее вычислим множитель

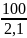= = 47,62

Обращаем внимание на то, что в первом и девятом интервалах

np_i= 3,067 < 5. Поэтому эти интервалы объединяем c соседними. Для объединенных интервалов полагаем равным соответственно 6+8=14 и 6+7=13, пр_i равным 3,067 + 6,833 = 9,9 (это значение записано после фигурной скобки в десятом столбце). После объе­динения крайних интервалов получилась новая группировка, содер­жащая 7 интервалов:

[13; 15), [15; 16), ... , [19; 20), [20;22).Значения 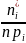для этих интервалов записываем в одиннадцатом столб­це. Складывая эти значения и вычитая из суммы n = 100, получим значение 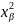= 7,5 (последняя строка в одиннадцатом столбце).

По таблице критических точек распределения х² ([3],c. 465) находим (k) , где 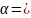0,05, а k = -3. В новой группировке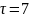 , следовательно, k = 7 - 3 = 4. При этих значениях и k из таблицы находим 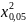(4) = 9,5. Сравнивая и (4), убеждаемся, что = 7,5 < 9,5 = (4). Следовательно, опытные данные не противоречат гипотезе о нормальном распределении исследуемой величины х с параметрами

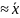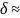m = 17,5 и s = 2,1.

5. Построение графика плотности и доверительных интервалов для параметров m и .

Так как гипотеза о нормальном распределении не отвергнута, сравним график плотности f(x)=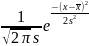 с гистограммой относительных частот. Для этого на чертеже гистограмм приближен­но построим график плотности, найдя значение f(x) в пяти точках х₁= = 17,5;

х_2,3 = S= 17,5 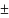2,1; x_4,5 = 2S = 17,5 4,2.

Имеем

f(x₁)= f ( )=f_max= ;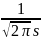

f (x_2,3)= f ( S)= ;

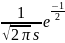f (x_4,5) = f( 2S) = .

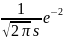Постоянные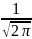 = 0,3989, 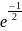= 0,6065 и 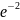= 0,1353 найдем заранее (они имеются во многих справочниках). Используя их, получим:

f(x₁)=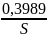 = =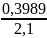0,19;

f (x_2,3)= f(x₁) =0,19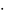 0,6065 = 0,115;

f (x_4,5)= f(x₁) = 0,19 0,1353 = 0,026.

Нанеся точки ( x_i; f (x_i)) на координатную плоскость и помня о том, что x₁ - точка максимума, а( x₂; f (x₂)) и ( x₃; f (x₃)) точки перегиба, соединим их плавной кривой. Получим приближенно график нормальной плотности с параметрами и S (рис. 2).

Из рисунка видно, что этот график хорошо согласуется с гистограммой.

Найдем, наконец, доверительные интервалы для и m=M (x) и = 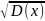, для чего используем формулы (4) и (5). Задав на­дежность 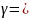0,95, по таблицам находим и q при n = 100 ([3], с.464). Имеем = 1,984. q= 0,143. Отсюда

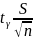= 1,984 2,1:10 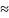0,42;

S (1 – q) = 2,1 (1 – 0,143) = 2,1 0,857 = 1,8;

S (1 + q) = 2,1 1,143 = 2,4.

Таким образом, доверительные интервалы имеют вид:

17,5 – 0,42 m 17,5 + 0,42, т.е. 17,08 m 17,02 и 1,8 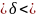2,4.

Сдано в РИО 21.08.87

Подп. в печать 21.08.87

Формат изд. 60 84 , 1/16, п.л. 0,8

Тираж 3000.Заказ 242.