33. 9. Ряди Тейлора і Маклорена

Дотепер визначали область збіжності степеневого ряду. Знаємо, що сума степеневого ряду неперервна в його області збіжності. Поставимо обернену задачу: за заданою неперервною функцією знайдемо степеневий ряд, що є збіжним, сума якого у всіх точках області збіжності збігається зі значеннями функції . Ця задача називається розвиненням функції в степеневий ряд.

Нехай неперервна функція зображена степеневим рядом в околі точки :

(7.26)

Права частина рівності (7.26) диференційована скільки завгодно раз, значить ліва частина цієї рівності, тобто функція також повинна бути диференційована скільки завгодно раз.

Це перша вимога, якій повинна задовольняти функція . Диференціюючи послідовно рівність (7.26), одержимо

...................................................................

.

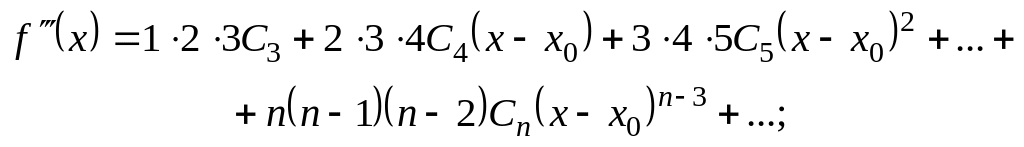
Підставляючи в ці рівності , маємо:

; ; ; ; ...; .

Звідки знаходимо

; ; ; ; ...; ,...

Підставляючи значення коефіцієнтів у рівності (7.26), одержуємо

(7.27)

Степеневий ряд, коефіцієнти якого рівні відповідно , називається рядом Тейлора.

При одержимо ряд за степенями , що називається рядом Маклорена.

Якщо функція в деякому околі точки є сумою степеневого ряду за степенями , то цей ряд є рядом Тейлора функції (при – відповідно рядом Маклорена функції ).

Але ряд Тейлора, складений для функції може і не бути збіжним до цієї функції в околі розглянутої точки .

Назвемо різницю між функцією і частковою сумою ряду Тейлора функції залишковим членом ряду Тейлора і позначимо

.

Теорема 7.4. Для того, щоб функція в околі точки була сумою складеного для неї ряду Тейлора, необхідно і достатньо виконання двох таких умов:

1) диференційована скільки завгодно раз;

2) .

Необхідність виконання першої умови очевидна. Необхідність виконання другої умови легко довести.

Нехай – сума ряду Тейлора, а – його частинна сума.

Тоді , .

Переходячи до границі при , одержуємо

, .

Аналогічно можна довести, що якщо має похідні будь-якого порядку в точці і її околі, і залишковий член ряду Тейлора для функції прямує до нуля при , то ця функція є сумою побудованого для неї ряду Тейлора.

Доведено, що залишковий член ряду може бути записаний у вигляді

, де .

Це одна з форм залишкового члена ряду (форма Лагранжа), яка дозволяє оцінювати його при .

34. 10. Розвинення функцій в ряд Маклорена

Щоб функцію розкласти в ряд Тейлора (зокрема, у ряд Маклорена), потрібно:

1. Знайти її похідні ;

2. Обчислити значення похідних у точці (для ряду Маклорена );

3. Формально скласти ряд Тейлора (Маклорена);

4. Знайти область збіжності отриманого ряду;

5. Дослідити залишковий член ряду при .

Якщо , то для функції справедлива рівність (7.26).

Розглянемо . Тоді: . Звідки одержуємо . Ряд Маклорена для функції має вигляд

.

Такий ряд збіжний на всій числовій прямій. Залишковий член ряду має вигляд , де . , тому що (як загальний член збіжного ряду). Тому справедлива рівність

. (7.28)

Розглянемо . Тоді

; ;

; ; ...

.

Підставляючи , одержуємо

.

Ряд Маклорена для функції має вигляд

.

Легко переконатися в тому, що такий ряд є збіжним на всій числовій прямій. Залишковий член ряду для функції : , де . при будь-якому x, тоді

(7.29)

Розвинення в ряд функції можна одержати шляхом диференціювання ряду для :

. (7.30)

Розглянемо , де – будь-яке дійсне число:

; ;

; ...

.

Обчислимо значення функції і її похідних:

, , , , ... .

Одержимо степеневий ряд

Тоді

. (7.31)

Формула (7.31) називається біноміальним рядом.

При маємо геометричний ряд

.

Замінивши в останній рівності на і, інтегруючи, одержимо розвинення в ряд функції

. (7.32)