§5 Основное уравнение молекулярно-кинетической теории идеальных газов.

Применим распределение Максвелла для вывода основного уравнения кинетической теории газов. Наша задача установить путем статистического усреднения микрохарактеристик молекул системы, некоторые макрохарактеристики, описывающие газ в целом. Известно, что давление газа создается за счет ударов молекул газа о стенки сосуда. Примем, что удар является абсолютно упругим и молекулы бомбардируют стенки как материальные точки под разными углами и с различными скоростями.

По второму закону Ньютона: , .

Молекулы ударяются о стенку и отскакивают, меняя только -составляющую скорости. Подсчитаем изменение -составляющей импульса всех молекул за время . Надо подсчитать поток импульса молекул в положительном направлении оси , т.е. м², с, поток – число частиц пролетающих за единицу времени через единичную площадку. В стенку ударятся только те молекулы, которые движутся к ней, а не от нее, т.е. . За время до стенки долетают все молекулы в объеме , .

Вероятность частиц иметь такую скорость , тогда число частиц, имеющих такую скорость .

Импульс, передаваемый стенке сосуда

, вычислим отдельно внутренний интеграл и подставим в выражение

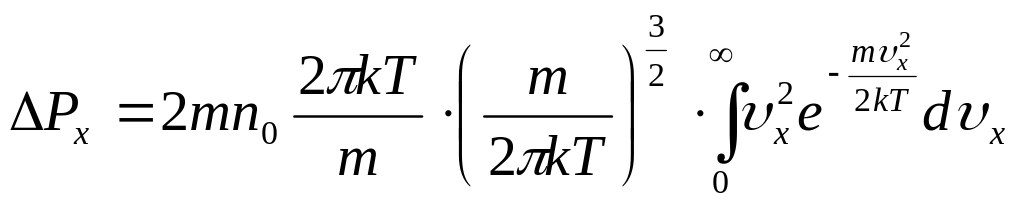, рассчитаем интеграл, сделав замену переменной,

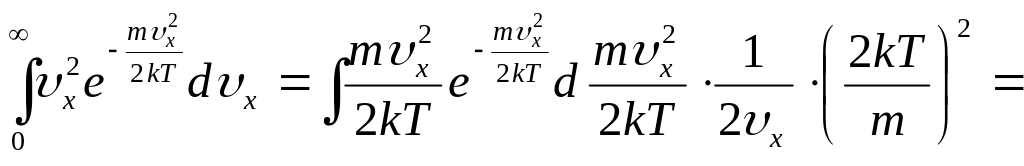
, , , отсюда , , , , , подставим полученное в интеграл:

. Таким образом давление на стенку

.

Аналогично для других стенок , с другой стороны , тогда , таким образом , - основное уравнение молекулярно-кинетической теории идеального газа.

Отсюда можно получить уравнение состояния идеального газа:

 - уравнение состояния идеального газа.

Если имеется смесь газов, то - закон Дальтона.

§6 Функция Больцмана

Плотность вероятности того, что молекула имеет положение в интервале – функция распределения Больцмана

Вероятность того, что частица находится в объеме , вблизи точки -

.

Определим зависимость плотности идеального газа в поле сил тяжести при изотермических условиях. Потенциальная энергия частицы в поле силы тяжести:

, , тогда число частиц в объеме ,

.

Масса частиц в объеме , отсюда

.

Пусть , тогда обозначив, - плотность на уровне моря, а , получим зависимость плотности от высоты .

Если учтем уравнение состояния идеального газа, то получим зависимость давления от

высоты получим  - барометрическая формула.

Используя распределение молекул по высоте Ж.Перрен экспериментально определил постоянную Авогадро. Он исследовал под микроскопом распределение броуновских частиц, т.е. считал под микроскопом число таких частиц на разных высотах в сосуде. Частицы были помещены в жидкость, плотность которой лишь на немного меньше плотности материала частиц, для того чтобы тяжелые частицы не «осели на дно», а распределились в достаточно большом слое по высоте.

, где - масса частицы, - масса вытесненной воды.

,  

.

§7 Распределение энергии по степеням свободы.

Среднее значение энергии одной молекулы . Если бы мы посчитали отдельно , то получили бы величину ровно в три раза меньшую, чем полная энергия. Такие же значения и для .

Таким образом, если вы молекула могла двигаться только вдоль оси , ее средняя энергия была бы . Говорят, что у молекулы, которая может совершать только одномерные движения – одна степень свободы: . Это значит. Что нужна только одна переменная, чтобы описать движение частицы. Для материальной точки таких переменных нужно 3: . Если же молекула может еще и вращаться, то число степеней свободы увеличивается. Средняя энергия, приходящаяся на одну степень свободы вращательного движения, а также на одну колебательную степень свободы (как потенциальной , так и кинетической) равна .

Теорема о равнораспределении энергии по степеням свободы: на все степени свободы статистической системы приходится одна и та же энергия . Это не относится к потенциальной энергии системы во внешних полях.

Средняя энергия одной молекулы , где число степеней свободы .

Р асхождение теории теплоемкости идеального газа с экспериментом.

Например, для некоторого количества идеального газа: , его молярная теплоемкость

Для двух атомных молекул всего может быть 3-поступательных, 2-вращательных, 1-колебательная степени свободы. По расчетам для водорода (идеального газа) теплоемкость не зависит от температуры .

Зависимость теплоемкости молекулярного водорода от температуры, полученная в ходе экспериментов, дается на графике .

Молекула водорода ведет себя при низкой температуре как точечная частица, у которой отсутствуют внутренние движения, при нормальной температуре – как жесткая гантель и наряду с поступательным движением также совершает вращательные движения, а при очень высокой температуре к этим движениям добавляются также колебательные движения атомов, входящих в молекулу. Объяснить эту зависимость классической теории не удалось.

Отличие экспериментальной кривой от теоретической прямой имеет квантовое объяснение. При низких температурах вращательные и колебательные степени свободы «выключены», т.е. они не возбуждаются. При температурах 116К могут возбуждаться вращательные степени свободы, а при температурах  4100К возбуждаются и колебательные степени свободы. Однако переход от одного режима движения к другому происходит не скачком при определенной температуре, а постепенно в некотором интервале температур. Это объясняется тем, что при определенной температуре возникает лишь возможность перехода молекул в другой режим движения, но эта возможность не реализуется сразу всеми молекулами, а лишь их частью.