3. Виды индексов и их свойства

Все экономические индексы можно классифицировать по многим признакам, которые отражают форму построения, степень охвата изучаемого явления признакам и т.п. Рассмотрим их более подробно.

1. По назначению (цели определения)

-динамические

-территориальные

-нормативные (выполнения плана)

2. По степени охвата явления

- индивидуальные ( по отдельному элементу)

-группповые (по группе элементов)

-сводные (по всем элементам)

3. По базе сравнения индексируемой величины в длительной динамике

- с постоянной базой (базисные)

- с переменной базой (цепные)

4. По характеру индексируемой величины

-индексы количественных показателей

-индексы качественных показателей

5. По форме построения индекса

- индексы агрегатной формы

-арифметические индексы

В.т. среднеарифметический

среднегармонический

6. По виду весов (соизмерителей)

- с постоянными весами

- с переменными весами

7. По составу явления

- постоянного состава

- индексы переменного состава

Рассмотрим виды на примере таблицы 6.1

Индивидуальные индексы показывают разные темпы изменения отдельных элементов и являются по своей сути коэффициентами роста. Их расчет представлен в таблице в 3 и 6 графах.

Групповой или субиндекс может быть получен по группе продукции животноводства. Индекс физического объема продукции составит или 100,3%.

Общий индекс был определен ранее и составил 1,142.

Индекс является средней величиной изменения по группе элементов (продуктов), то есть средней взвешенной из индивидуальных индексов. Весами при расчете арифметического индекса является сумма стоимости продукции отдельных видов . Средний арифметический индекс рассчитывается по формуле , где - индивидуальные индексы. Численно он равен агрегатному индексу , так как , а .

Общий индекс цен оможет быть рассчитан по формуле средней гармонической 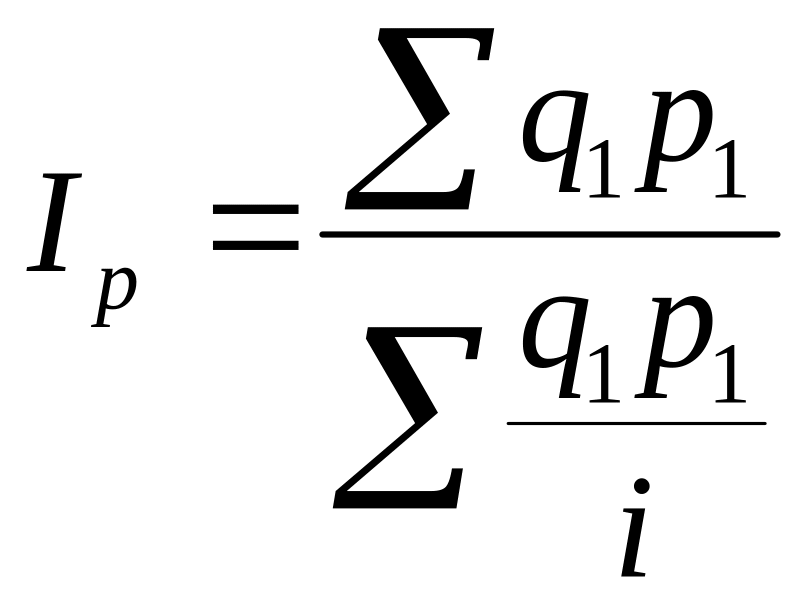. Этот индекс равен агрегатному индексу цен , так как неизвестная цена .

Основной формой индекса являются агрегатные индексы. К средним арифметическим и другим формам индексов прибегают в зависимости от характера исходных данных (при известных индивидуальных индексах объема продукции и неизвестных и ).

Динамические индексы, как и коэффициенты роста в рядах динамики, бывают цепными и базисными. В цепных индексах сопоставляются последовательно два агрегата за смежные годы, а в базисном изучаемые уровни явления за крайний год (или другой период времени) по сравнению с одним и тем же базисным.

Рассматриваемый в примере индекс физического объема продукции является базисным, так как отчетное количество относится к 2002 году. Т.е. , а базисное – к 1998 году ( ). Этот индекс . Наряду с ним могут быть рассчитаны цепные индексы при оценке продукции двумя способами:

1. При сохранении цен за базисный период, то есть при

. Произведение цепных индексов равно базисному индексу крайних уровней ряда. По приведенным в таблице 6.1 продуктам эти индексы в России составили: 1,068 × 1,357 × 0,850 × 0,927 = 1,142.

При оценке количества продукции по ценам предыдущего года, то есть по , где n – конечный уровень:

.

Полученные индексы называют индексами с переменными весами в отличие от первого случая, когда получают индексы с постоянными весами. Очевидно, что произведение цепных индексов с переменными весами не равно базисному индексу.

Если индекс рассчитан по одинаковому набору продукции, его называют индексом фиксированного или постоянного состава. В индексах постоянного состава всегда изменяется только одна (индексируемая) величина.

В индексах переменного состава изменяются две и более величины. Это индексы стоимостного объема продукции, индексы средних уровней. Они обладают свойством раскладываться на индексы постоянного состава. Например, индекс стоимостного объема раскладывается на индекс цен и физического объема.

Это свойство положено в основу индексного метода анализа.

Индексы средних уровней качественных показателей

В статистике широко используются индексы средних уровней признаков X: , где - средний уровень изучаемого (отчетного) признака, а - базисное значение за прошлый период, по другой совокупности, по плану и т.п. Средние уровни могут быть рассчитаны по группе однородных и разнородных элементов q или Q. Рассмотрим вначале индекс среднего уровня по однородной совокупности элементов, поддающихся непосредственному суммированию, на примере реализации мяса и мясопродуктов в сельскохозяйственных организациях, учтенных МСХ РФ (табл. 6.2).