Нахождение частного решения лнду 2 порядка с постоянными коэф. В случае правой части вида
Пусть
правая часть уравнения
(1) имеет вид
,
где
– многочлен n-ной
степени: 
(2) Тогда возможны следующие случаи:
а)
Число
не является корнем характеристического
уравнения
(3)Тогда частное решение уравнения (2)
будем искать в виде
(4) Подставим его в (2) с учетом вида
производных
и сокращая на
,
получим:
(5) Если
не является корнем характеристического
уравнения, то
и слева в уравнении (5) – полином n-ного
порядка, приравнивая коэффициенты при
равных степенях х
слева и справа в (5), получим n+1
уравнение с n+1
неизвестной
,
найдем их и получим частное решение
(4).
б)
Число
есть однократный корень характеристического
уравнения (3) (резонанс). Тогда в уравнении
(5) не будет
,
и слева - полином (n+1)-й
степени, а справа – n-й
степени, и мы не сможем его найти. В этом
случае частное решение ищется в виде
(6)
в)
Число
есть двукратный корень характеристического
уравнения,
.
Тогда в уравнении (5)
и слева- полином (n-2)
степени, а справа- n-й
степени. Частное решение будем искать
в виде
(7)
Нахождение частного решения лнду 2 порядка с постоянными коэф. В случае правой части вида . Важный частный случай
Пусть
уравнение
(1) имеет вид:
(2)где
- многочлены. Рассмотрим два случая:
а)
Если число
не является корнем характеристического
уравнения, то частное решение уравнения
(2) надо искать в виде
(3) где
–
многочлены степени, равной наивысшей
степени многочленов
и
.
б)
Если число
есть корень характеристического
уравнения, то частное решение ищем в
виде
(4)
Важный
частный случай:
если
,
где M,
N-
постоянные числа, т.е.
(5)
а)
Если число
- не является корнем характеристического
уравнения, то частное решение ищем в
виде
(6)
б)
Если
- корень характеристического уравнения,
то частное решение уравнения (5) ищем в
виде
(7)
Решение лнду методом вариации произвольных постоянных
Пусть
общее решение однородного уравнения
(1)имеет вид
(2) Будем искать общее решение неоднородного
уравнения
(3) в виде (2), считая
и
функциями х,
т.е.
(4) Здесь
.
Подберем искомые функции
и
так, чтобы выполнялось равенство
(5) Тогда
,
подставляем в (5) и получим:
Итак, функция (4) будет решением
неоднородного уравнения (3), если
выполняются условия:
Решая эту систему относительно
,
получим:
,
Интегрируя эти равенства, получим:
;
Подставляя их в (4), получим общее решение
уравнения (3).
Системы обыкновенных диф. Урав.
При
решении многих задач требуется найти
функции
,
удовлетворяющие следующим уравнениям:
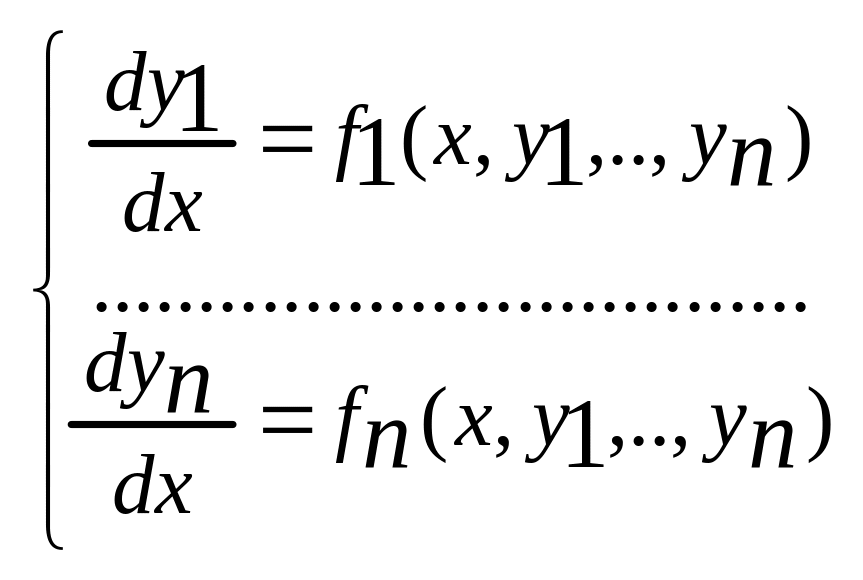(1) (нормальная система) Проинтегрировать
эту систему - значит получить функции
,
удовлетворяющие уравнениям (1) и начальным
условиям
(2) Идея решения – исключить из одного
уравнения все переменные, кроме одной,
проинтегрировать его, подставить решение
в другие уравнения и т.д. Продифференцируем
первое уравнение по х:
Здесь исключим
с помощью (1), получим:
Аналогично получим:
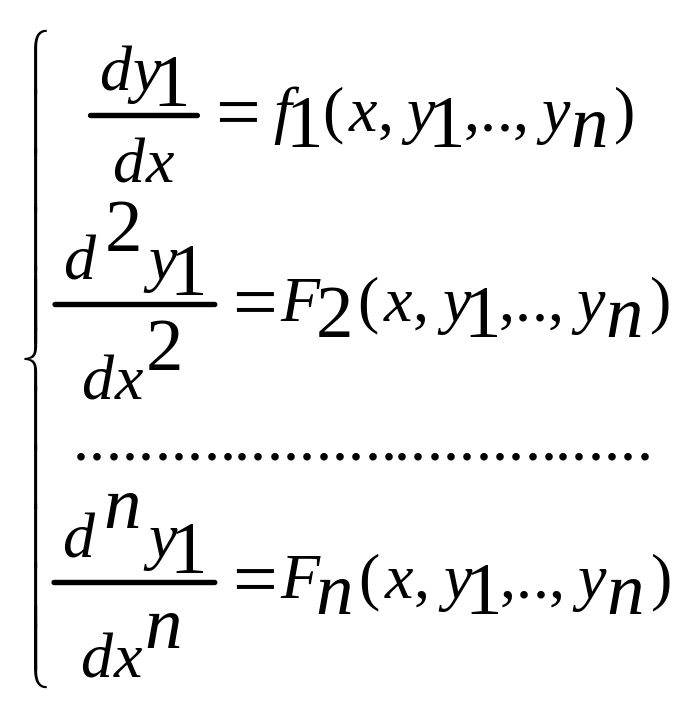(3) Из первых (n-1)
уравнений выражаем
через
:
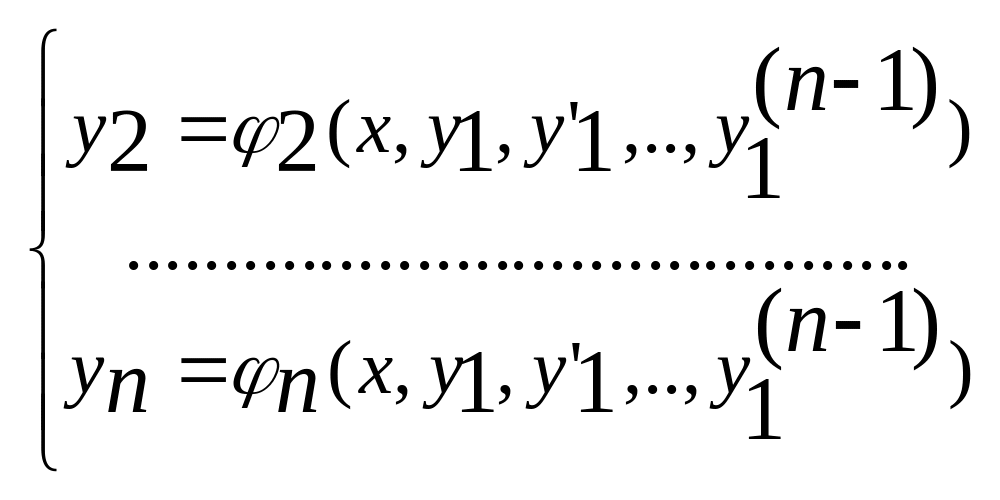(4)
и подставляем в последнее уравнение:
(5) Решая это уравнение, получим:
(6) подставляя это решение и его производные
в (4), получим остальные функции:
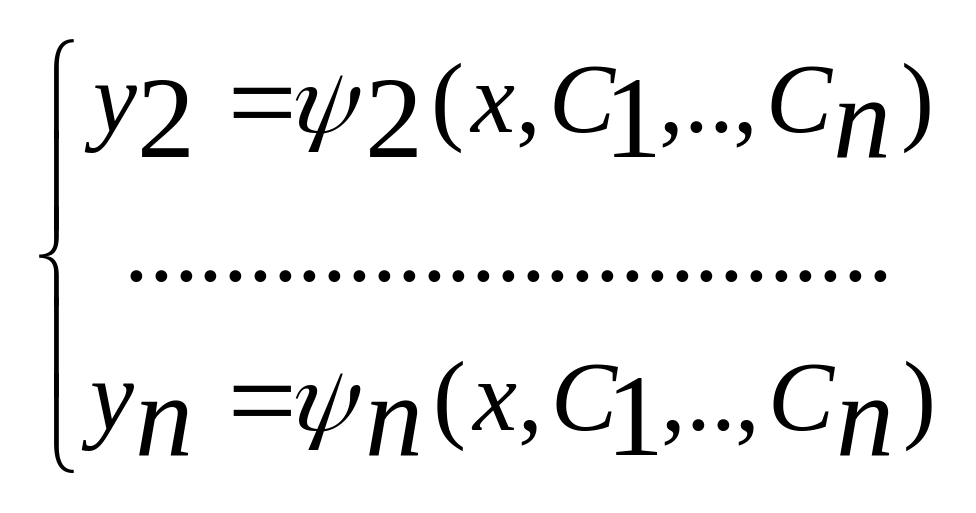(7) Здесь константы
можно найти с помощью начальных данных
(2).