7.2Критерий Гурвица

Это алгебраический критерий, по нему можно судить об устойчивости системы на основании исследования ряда неравенств, связывающих коэффициенты характеристического уравнения.

Для применения критерия Гурвица характеристическое уравнение записывается при таком виде, чтобы а₀ >0.

Коэффициенты уравнения располагают в виде определителя Гурвица.

Определитель содержит n-столбцов. Запись определителя начинается с заполнения главной диагонали. В левом верхнем углу записывается а₁, а в правом нижнем а_n.

Ниже записываются коэффициенты, которые стоят левее, а выше те, которые правее. Остальные приравниваются к нулю.

Критерий устойчивости системы: Определитель Гурвица и все миноры должны быть положительные.

Передаточная функция системы имеет вид:

А ее характеристическое уравнение с коэффициентами:

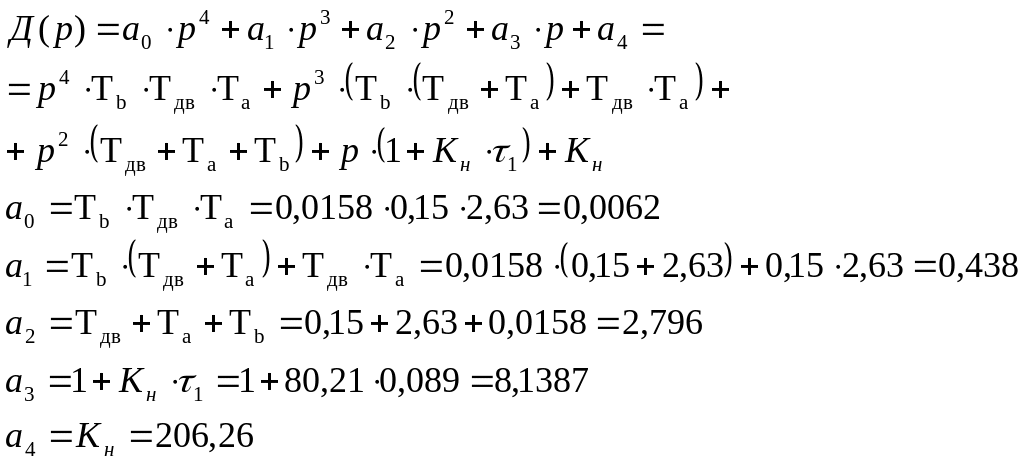
Критерий Гурвица примет вид:

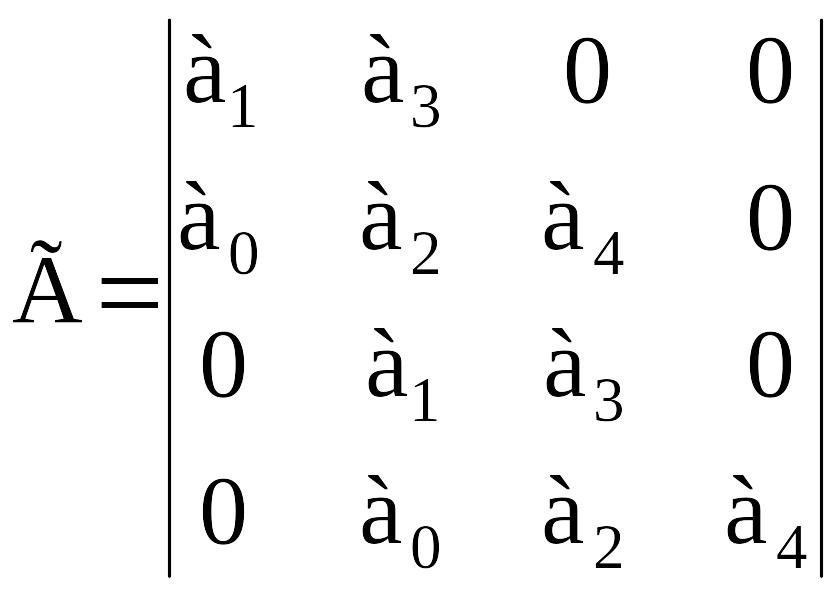
Раскрывая его получим следующую систему:

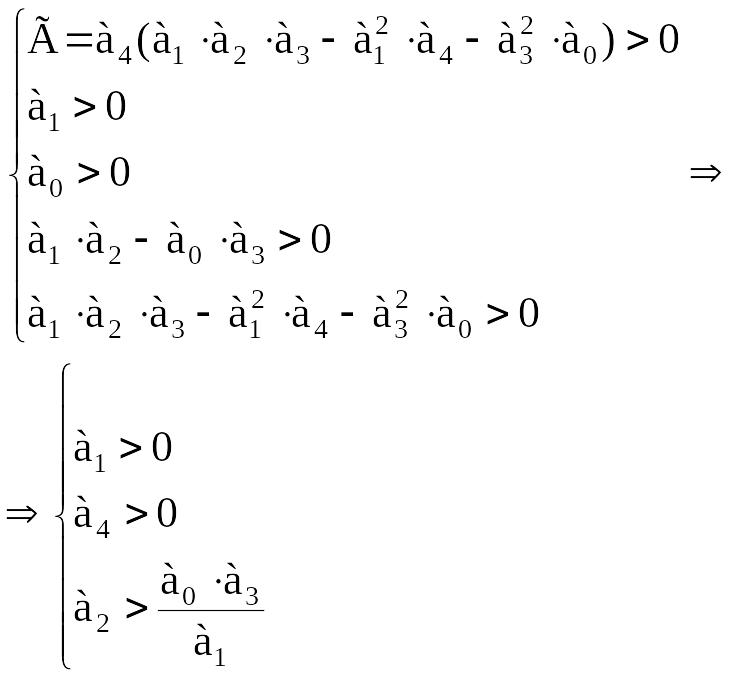
Проверим систему по критерию Гурвица:

Следовательно, проверка по критерию Гурвица показала что система устойчива.

7.3Критерий Михайлова.

Подставим в характеристический многочлен вместо оператора Р оператор jω:

Найдем корни характеристического уравнения Р_1, Р_2,… Р_n, ,тогда характеристический многочлен можно разложить на множители:

.

Критерий Михайлова основан на исследовании изменения аргумента вектора Д(jw). Аргумент вектора Д(jω) представляет собой сумму аргументов вектора всех сомножителей:

.

При изменении параметра ω от нуля до бесконечности конец вектора D(jω) описывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова. Рассмотрим изменение аргумента вектора отдельных сомножителей при изменении оператора ω от нуля до бесконечности

а) Пусть Р₁ является отрицательным и действительным , тогда получим уравнение:

.

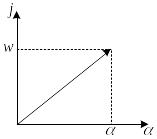
Рисунок 10

,если w=0, argA₁=0 .

б) Пусть Р₁ является положительным и действительным Р₁ = , тогда получим уравнение:

.

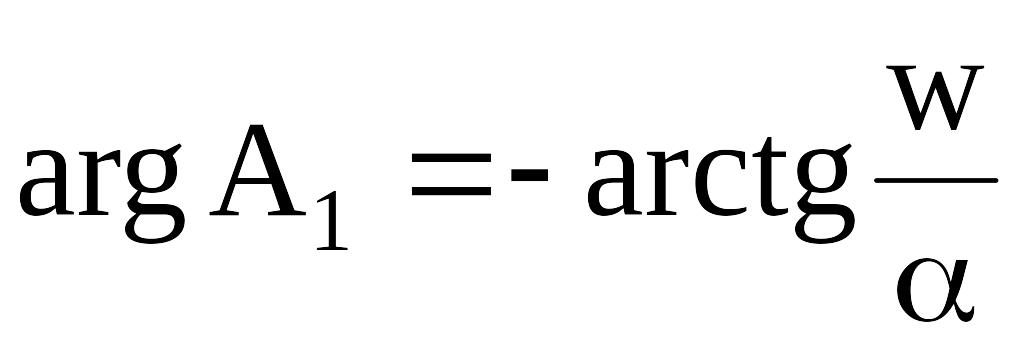, если .

Вывод: каждый положительный действительный корень обеспечивает поворот вектора Д(jw) на угол

Аналогично можно показать, что комплексно сопряженный корень при увеличении оператора ω от 0 до бесконечности в случае отрицательной действительной части даст суммарный поворот на угол равный +. При положительной действительной части суммарный поворот будет составлять –.

Рассмотрим систему n-го порядка. Общее число корней характеристического уравнения будет равно n. Пусть среди них будет l корней с положительной действительной частью, тогда n-l – число корней с отрицательной действительной частью. В этом случае при изменении оператора w от нуля до бесконечности поворот вектора Д(jw) составит – положительный поворот, а – отрицательный поворот.

Если система устойчива, то характеристическое уравнение не должно содержать корней с действительной частью, следовательно, для устойчивой системы:

Конец вектора D(jw) при изменении ω от 0 до бесконечности опишет некоторую, называемую кривой (годографом) Михайлова.

Кривая Михайлова начинается на вещественной оси при w = 0 в точке X(0)= = a_n, jY(0) = 0 и заканчивается в n-м квадранте, если отсчет квадрантов вести против часовой стрелки. В n-м квадранте кривая Михайлова уходит в бесконечность.

Чтобы построить кривую Михайлова, необходимо в выражении Д(jw) разделить действительную и мнимую части. Далее, задаваясь различными значениями w = 0, w₁, w₂,…, необходимо найти точки [X(0);jY(0)]; [X(w₁);jY(w₁)]; [X(w₂);jY(w₂)];…

Анализируя годографы сложно сделать вывод, что у устойчивой системы годограф Михайлова поочередно пересекает ось действительных и мнимых чисел, последовательно проходя через n квадратов, где n – порядок САУ.