
- •Курс лекций “Численные методы”
- •8.5 Численное интегрирование жестких систем
- •1 Условно устойчивые и абсолютно устойчивые разностные методы
- •2 Понятие жесткой системы дифференциальных уравнений
- •3 Нелинейные системы дифференциальных уравнений
- •4 Специальные определения устойчивости
- •5 Чисто неявные разностные методы
3 Нелинейные системы дифференциальных уравнений
Обобщим понятие жесткости на случай нелинейной системы
, , (8.74)
где
![]() ,
,
![]() .
.
Зафиксируем
какое-либо решение
![]() системы (8.74) и образуем разность
системы (8.74) и образуем разность
![]() между решением системы (8.74) и данным
решением
.
Эта разность удовлетворяет следующей
системе уравнений:
между решением системы (8.74) и данным
решением
.
Эта разность удовлетворяет следующей
системе уравнений:
![]() ,
,
![]() .
(8.75)
.
(8.75)
Будем рассматривать
![]() как малое возмущение, внесенное в решение
.
Проведем разложение по формуле Тейлора
в правой части системы (8.75). Так как
как малое возмущение, внесенное в решение
.
Проведем разложение по формуле Тейлора
в правой части системы (8.75). Так как
![]() ,
,
имеем
![]() ,
,
где через
![]() обозначены величины второго порядка
малости по
обозначены величины второго порядка
малости по
![]() .
В результате разложения система (8.75)
примет вид
.
В результате разложения система (8.75)
примет вид
![]() ,
(8.76)
,
(8.76)
где через
![]() обозначена матрица с элементами
обозначена матрица с элементами
![]() ,
,
![]()
Отбрасывая в (8.76) величины , получим так называемую систему уравнений первого приближения
![]() .
(8.77)
.
(8.77)
Система (8.77)
является системой линейных дифференциальных
уравнений относительно
![]() ,
так как функция
задана.
,
так как функция
задана.
Определение жесткости системы нелинейных дифференциальных уравнений связано как с данным фиксированным решением , так и с длиной отрезка интегрирования
Пусть
,
собственные
числа матрицы
![]() .
.
Число жесткости
![]() определяется как
определяется как
.
Система (8.74)
называется жесткой на решении
и на данном интервале
![]() ,
если
,
если
1) , , для всех ,
2) велико.
4 Специальные определения устойчивости
При исследовании разностных методов для жестких систем уравнений обычно рассматривают уравнение
![]() ,
(8.78)
,
(8.78)
где
![]() произвольное
комплексное число. Свойства различных
разностных методов изучают и сопоставляют
на примере модельного уравнения (8.78).
Для того чтобы уравнение (8.78) действительно
моделировало исходную систему
произвольное
комплексное число. Свойства различных
разностных методов изучают и сопоставляют
на примере модельного уравнения (8.78).
Для того чтобы уравнение (8.78) действительно
моделировало исходную систему
![]() ,
,
необходимо
рассматривать его для всех таких
![]() ,
которые являются собственными числами
матрицы
.
,
которые являются собственными числами
матрицы
.
Разностный метод (8.64)
, , (8.64)
примененный к уравнению (8.78), имеет вид (доказать)
![]() ,
,
(8.79)
,
,
(8.79)
где
![]() комплексный
параметр.
комплексный
параметр.
Если искать решение
уравнения (8.79), имеющие вид
![]() ,
то для
получим характеристическое уравнение
,
то для
получим характеристическое уравнение
![]() ,
(8.80)
,
(8.80)
отличающееся от уравнения (8.65)
(8.65)
тем, что его
коэффициенты зависят от параметра
![]() .
При малых
.
При малых
![]() корни уравнения (8.65) и (8.79) близки. Однако
в дальнейшем мы не будем делать
предположений относительно малости
.
корни уравнения (8.65) и (8.79) близки. Однако
в дальнейшем мы не будем делать
предположений относительно малости
.
Кроме обычного
определения устойчивости разностного
метода (все корни характеристического
уравнения (8.79) не превосходят по модулю
единицу
),
в случае жестких систем используют и
другие, более узкие определения
устойчивости. В данном случае рассмотрим
![]() устойчивый
метод.
устойчивый
метод.
Введем следующее понятие. Областью устойчивости разностного метода (8.64)
, . (8.64)
называется множество точек комплексной плоскости , для которых данный метод, примененный к уравнению (8.78)
, (8.78)
является устойчивым.
Рассмотрим, например, явный метод Эйлера
![]() .
.
В применении к уравнению (8.78) этот метод принимает вид (доказать)
![]() ,
,
![]() .
.
Условие устойчивости
![]() для комплексного
для комплексного
![]() означает, что
означает, что
![]() .
Тем самым область устойчивости данного
метода представляет собой круг единичного
радиуса с центром в точке
.
Тем самым область устойчивости данного
метода представляет собой круг единичного
радиуса с центром в точке
![]() .
Для неявного метода Эйлера
.
Для неявного метода Эйлера
![]()
областью устойчивости
является внешность круга единичного
радиуса с центром в точке
![]() (доказать).
(доказать).
Разностный метод
называется
устойчивым,
если область его устойчивости содержит
левую полуплоскость
![]() .
Отметим, что уравнение (8.78) асимптотически
устойчиво при
.
Отметим, что уравнение (8.78) асимптотически
устойчиво при
![]() .
Поэтому сущность приведенного определения
состоит в том, что
устойчивый
разностный метод является абсолютно
устойчивым (устойчивым при любом
.
Поэтому сущность приведенного определения
состоит в том, что
устойчивый
разностный метод является абсолютно
устойчивым (устойчивым при любом
![]() ),
если устойчиво решение исходного
дифференциального уравнения.
),
если устойчиво решение исходного
дифференциального уравнения.
Нетрудно видеть, что неявный разностный метод Эйлера является устойчивым, а явный метод Эйлера – не является.
Рассмотрим одношаговый метод второго порядка точности
![]() .
(8.81)
.
(8.81)
Для уравнения (8.78) метод принимает вид (доказать)
![]() ,
откуда
,
откуда
![]() .
.
Отсюда видно, что
![]() тогда и только тогда, когда
(доказать).
Следовательно, метод (8.81) является
устойчивым.
тогда и только тогда, когда
(доказать).
Следовательно, метод (8.81) является
устойчивым.
При решении жестких систем уравнений желательно пользоваться именно устойчивыми разностными методами, так как условия их устойчивости не накладывают ограничений на шаг . Оказывается, однако, что класс устойчивых методов весьма узок. В частности, среди методов вида (8.79) не существует явных устойчивых методов.
Для доказательства запишем характеристическое уравнение (8.80)
, (8.80)
в виде
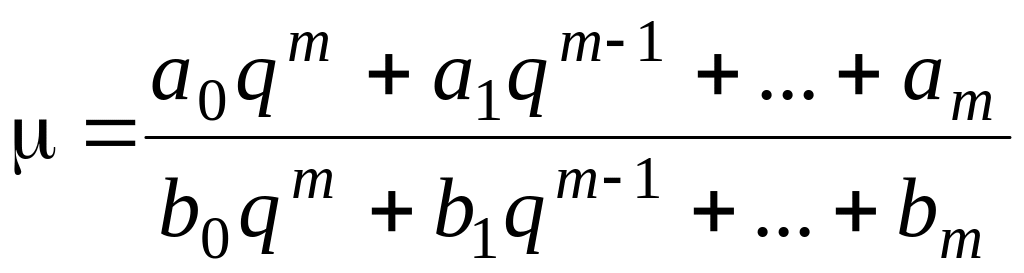 .
(8.82)
.
(8.82)
Если (8.79) ‑ явный
![]() -шаговый
метод, то
-шаговый
метод, то
![]() ,
,
![]() .
Могут оказаться равными нулю и другие
коэффициенты
.
Могут оказаться равными нулю и другие
коэффициенты
![]() ,
но не все, так как по условию
,
но не все, так как по условию
![]() .
Пусть
.
Пусть
![]() ,
,
![]() ,
,
![]() .
Тогда из (8.82) получим
.
Тогда из (8.82) получим
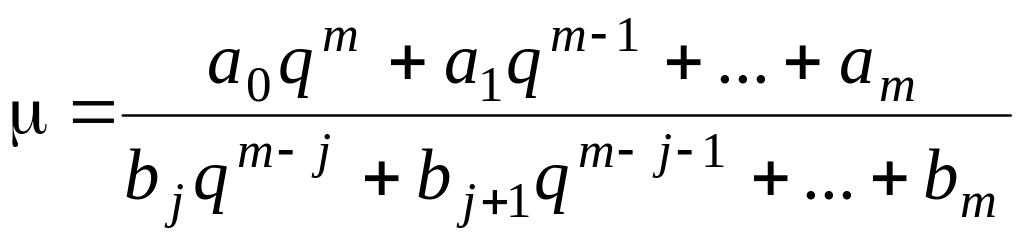 .
.
Отсюда видно, что
при больших
функция
![]() ведет себя как
ведет себя как
![]() ,
,
![]() .
.
Следовательно,
для любого достаточно большого по модулю
числа
,
в том числе, и для
,
лежащих в левой полуплоскости, найдется
корень
уравнения (8.80) с
![]() .
.
Можно доказать, что среди неявных линейных многошаговых методов нет устойчивых методов, имеющих порядок точности выше второго. Примером устойчивости метода второго порядка точности является симметричная схема (8.81).
