1. Тема: Определение положения центра тяжести.

2. Время: 2 часа (акад).

3. Место проведения: учебная аудитория.

4. Содержание Введение.

Цель работы – овладение различными методами определения положения центра тяжести твердого тела, изучение понятия об устойчивости равновесия.

Содержание работы – определение положения центра тяжести сечения и твердого тела и исследование устойчивости равновесия.

Теоретические сведения.

Понятие центра тяжести является одним из важнейших в механике.

Центром тяжести тела называют центр системы параллельных сил, которую приближенно образуют силы тяжести его элементарных частиц. Радиус-вектор центра тяжести можно вычислить по формуле

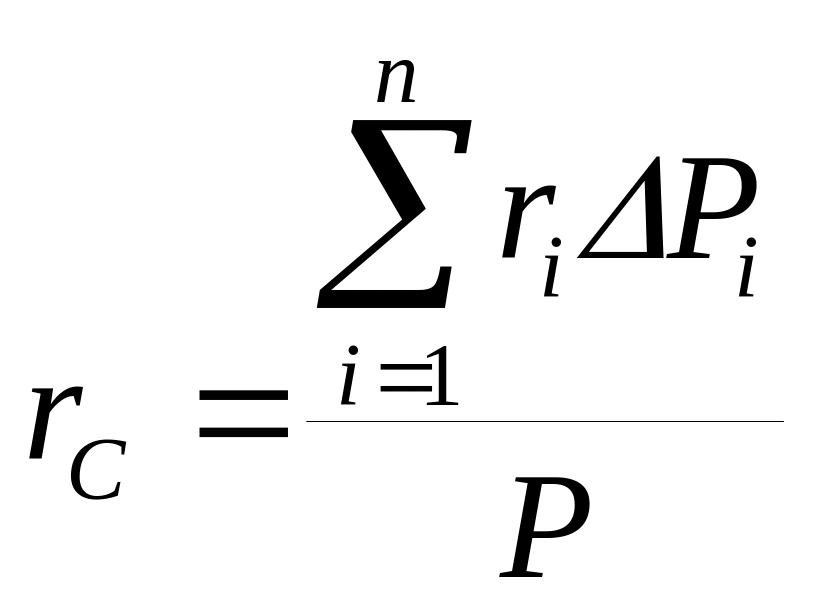(1)

где — радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку, — сила тяжести элементарной частицы, — сила тяжести всего тела, — число частей на которые разбито тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести его отдельных частей считать системой параллельных сил.

Для однородного тела вес любой его части пропорционален объему этой части: , а вес тела пропорционален объему всего тела, т.е. , где – вес единицы объема.

Подставив эти формулы в (1), получим координаты центра тяжести объема

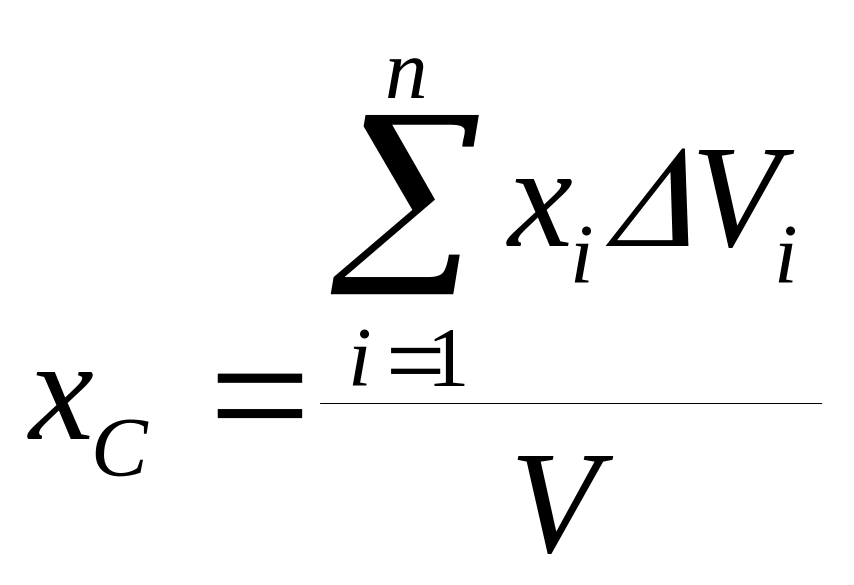
(2)

Аналогично для тела, представляющего собой однородную плоскую и тонкую пластину справедливы формулы

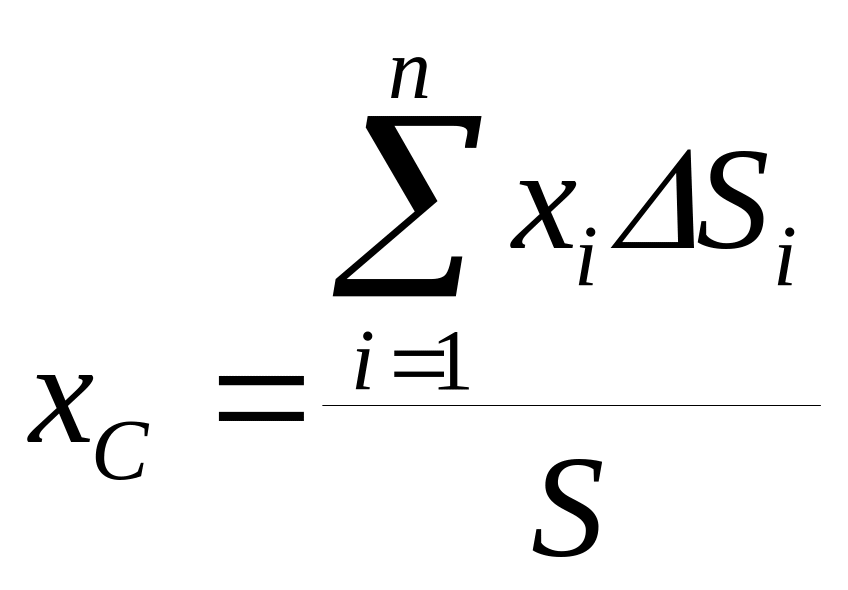
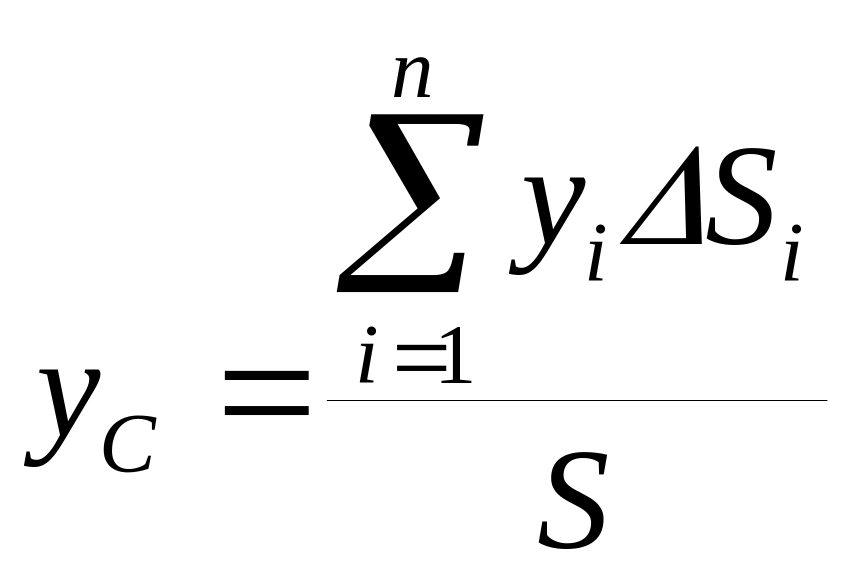
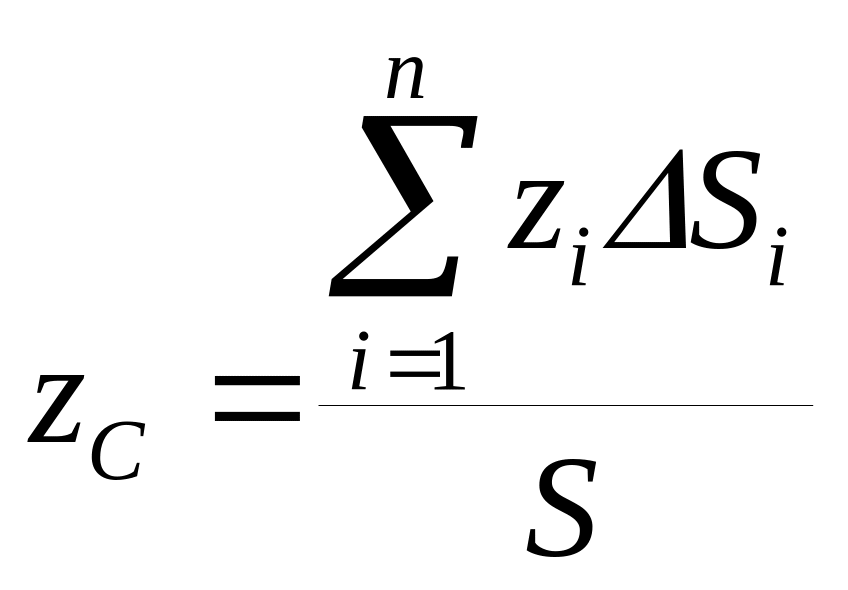(3)

Точно также получаются формулы для координат центра тяжести линии:

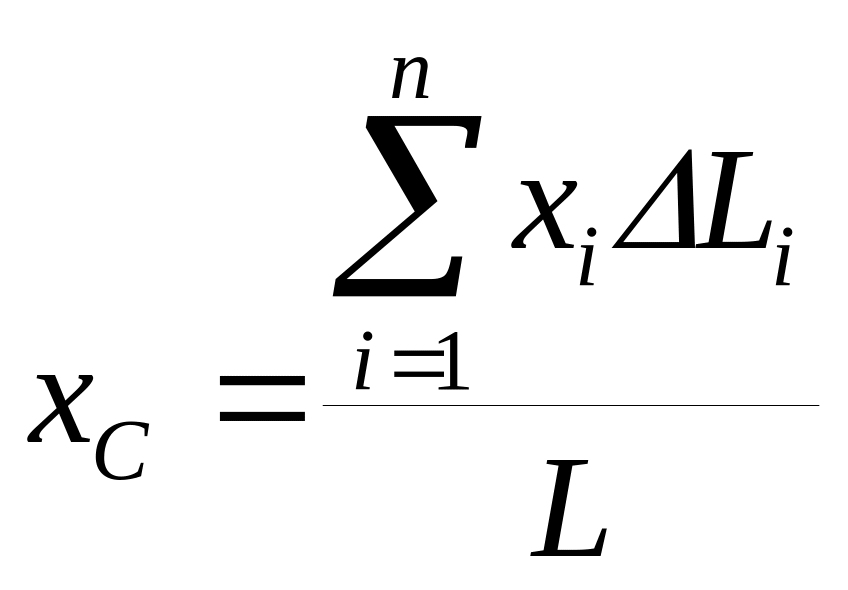
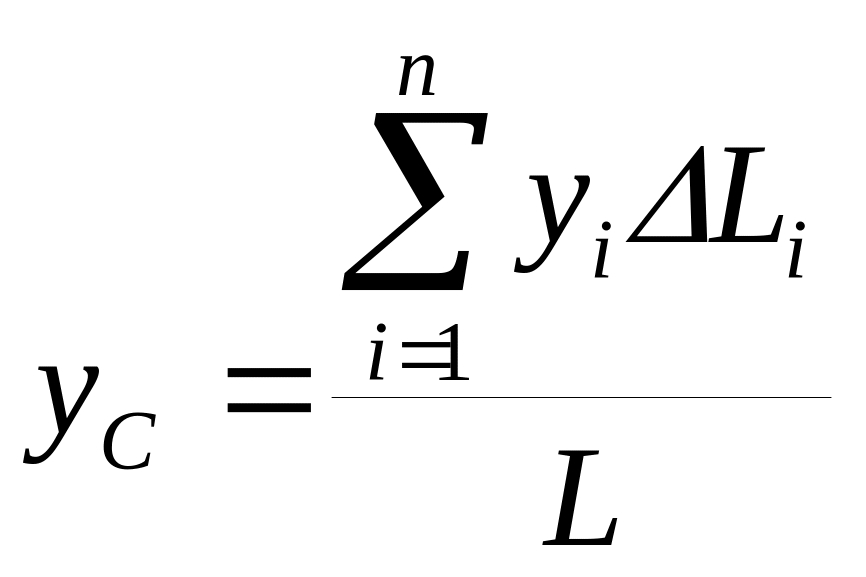
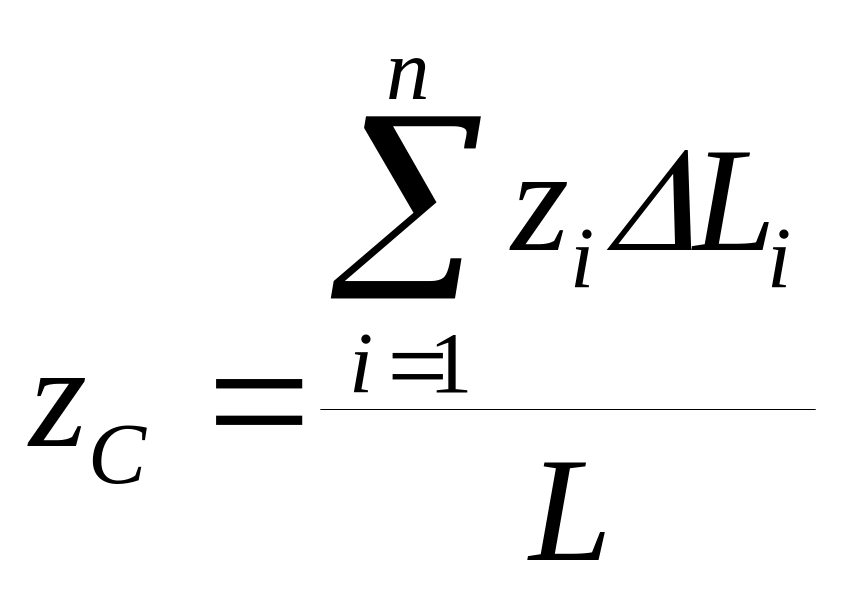(4)

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

Способы определения координат центров тяжести тел.

Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам (2)-(4). При этом число слагаемых в каждом из числителей будет равно числу частей, на которые разбито тело. Т.о.

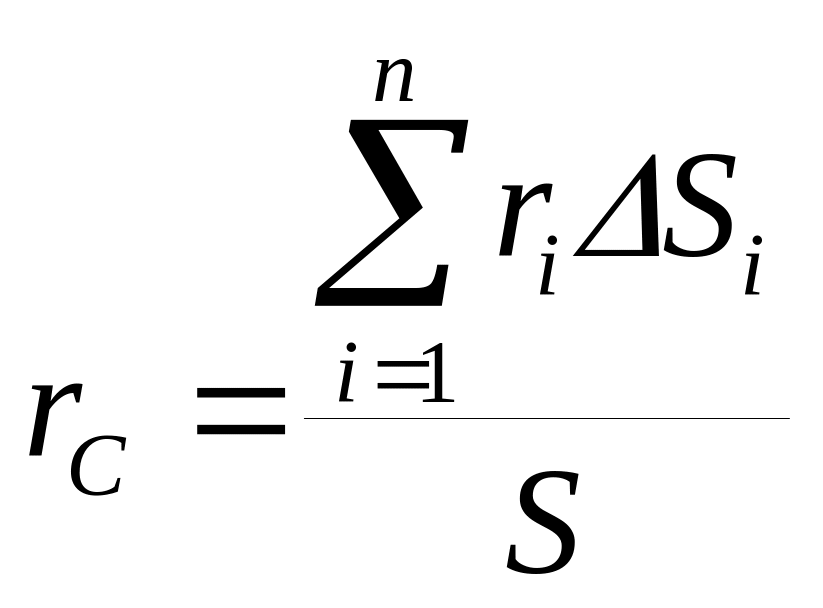(5)

Дополнение. Этот метод используется при вычислении центров тяжести тел, имеющих отверстия. В этом случае исходное тело дополняют до целого, при этом, в отличие от обычного метода разбиения площадь дополнительной части берется в формуле (5) со знаком минус.

Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело сначала разбивают на произвольные малые объемы, затем в формулах (1)-(4) переходят к пределу, стягивая все объемы в точку. Тогда имеем

(6)

Аналогичные формулы можно получить для координат центров тяжестей площадей и линий.

Понятие об устойчивости равновесия. Для тела, закрепленного наложенными связями не жестко, возникает вопрос об устойчивости равновесия. Если действующие силы стремятся вернуть тело в положение равновесия ( когда оно из этого положения выведено), то рассматриваемое положение равновесия является устойчивым, в противном случае равновесие будет неустойчивым. Практически тело может находиться в равновесии только когда положение равновесия устойчиво.

Характер равновесия можно исследовать, используя условия равновесия тела (см. лаб. раб. 1). При этом справедливо следующее утверждение: равновесие тела считается устойчивым, если его центр тяжести занимает наинизшее положение, и неустойчивым – когда наивысшее.

Рассмотренный метод исследования применим лишь в простейших задачах. Более сложные случаи исследуются динамическими методами.