§11 Парна лінійна регресія
11.1 Основні поняття: адекватність моделі; детермінація; значущість коефіцієнта; інтервали надійності; кореляція; регресія
11.2.
Розглянемо
модель, що встановлює лінійну залежність
між двома змінними: одна змінна
вважається залежною від іншої
.
Задані вектори спостережень
,
(або таблиця значень). Залежність
(
,
-
параметри), що характеризує середнє
значення показника
для значення фактора
називають регресією. Справжні значення
параметрів встановити не можна, тому
що
,
- випадкові величини, вектор помилок,
характеризує відхилення по осі
спостережувальних точок від лінії
регресії. Здобуті розрахунки значення
параметрів будуть статистичними оцінками
.
Одна
з основних задач економетрії : на підставі
статистичних даних показника
і фактора
дослідити
залежність між двома змінними.
Алгоритм дослідження наступний:
1.
Знайти оцінки параметрів лінійної
регресії
за допомогою метода найменших квадратів:
2. Знайти оцінки коефіцієнта кореляції
,
,
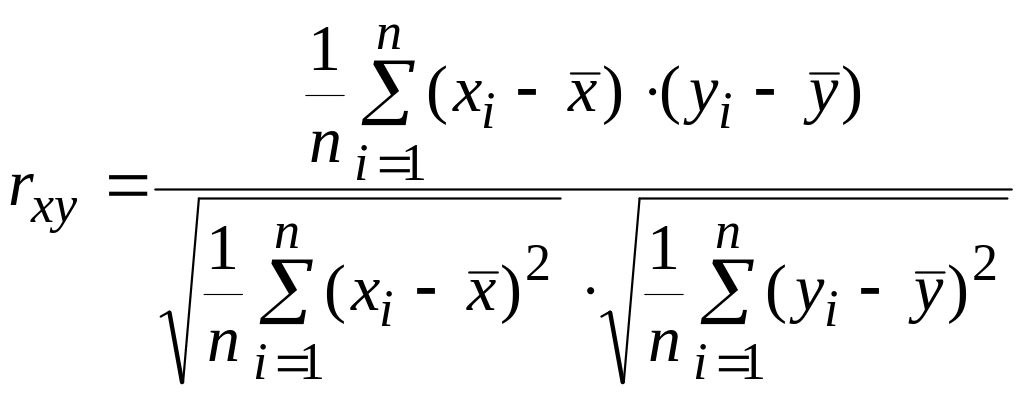3. Обчислити коефіцієнт детермінації за формулою
,
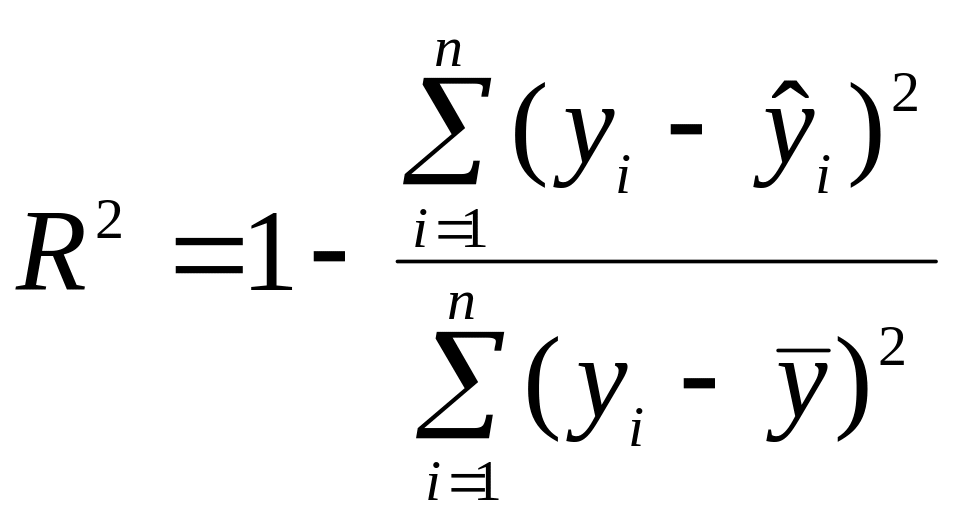Коефіцієнт детермінації показує, яка частина варіації залежної змінної обумовлена змінними факторами, тобто оцінюється адекватність моделі.
Зробити висновок про тісноту зв’язку.
4.
Використовуючи
критерій Фішера, з надійністю
оцінити адекватність прийнятої
економічної моделі статистичним даним
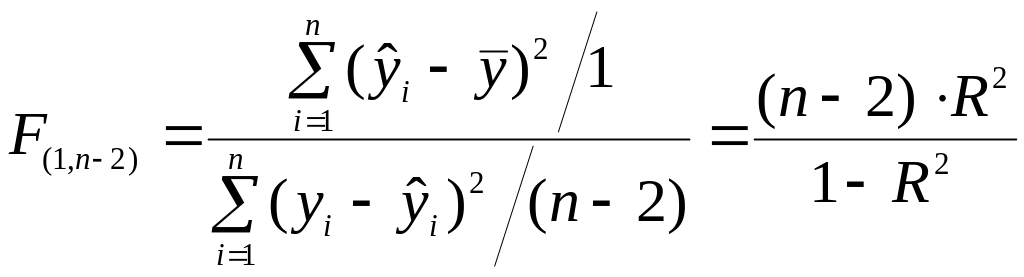
порівняти
з табличним значенням
для
(або
)
з ступенями вільності
і
.
Якщо
модель
адекватна реальній дійсності
5. Використовуючи t – статистику з надійністю (критерій Стьюдента) оцінити значущість коефіцієнта кореляції
Порівняти
з табличним значення
для розподілу Стьюдента з
і
.
Якщо
,
то коефіцієнт кореляції значущій.
6. Знайти надійні інтервали для регресії.
По таблиці знайти коефіцієнт Стьюдента (пункт 5)
.
Обчислити
,
,
де
.
Побудувати
на графіку надійну зону: з’єднати
неперервними лініями на графіку значення
,
- одна лінія
та
- друга лінія. Це і буде надійна зона.
7.
Знайти
прогноз показника
,
якщо потрібно і можливо.
8. На основі економетричної моделі зробити висновки.
11.3 Тести
11.1 Вибірковий коефіцієнт множинної детермінації обчислюється за формулою:
а)
;
б)
;
в)
;
г)
;
11.2
Для
парної регресії
має
ступенів вільності:
а)
1; б) 2; в)
;
г)
;
11.3 Для парної регресії має ступенів вільності:
а)
;
б)
;
в) 2; г)
;
11.4 Для парної регресії має ступенів вільності:
а) ; б) ; в) 1; г)
11.5 Якщо значення коефіцієнта кореляції між змінними x та y більше або 0,75, то це означає, що:
а) зв'язок між x та y тісний; б) зв'язок між x та y слабкий;
в) статистично значущого зв’язку між змінними немає.
г) зі збільшенням х значення у зростає.
11.6 Якщо значення коефіцієнта кореляції між змінними х та у дорівнює 0, то це означає, що:
а) зв'язок між х та у відсутній; б) зв'язок між x та y тісний;
в) зі збільшенням х значення у зростає;
г) зі збільшенням х значення у зменшується.
11.7 Модель парної регресії має вигляд:
а)
;
б)
;
в)
;
г)
.
11.8
Коефіцієнт
детермінації
вимірює:
а) загальну варіацію залежної змінної у, яка пояснюється регресією факторів, включених у модель;
б) нахил лінії регресії;
в) перетин лінії регресії з віссю ординат;
г) суттєвість включених у модель факторів.
11.9
Коефіцієнт
лінійної моделі
розраховується за формулою:
а)
;
б)
;
в)
;
г)
.
11.10 У випадку парної лінійної регресії від знака коефіцієнта кореляції:
а) залежить напрямок кореляційного зв’язку факторів і показника;
б) не залежить напрямок кореляційного зв’язку факторів і показника;
в) залежить тіснота зв’язку між фактором і показником;
г) нічого не залежить.
11.11 Вільний член у рівнянні регресії - це:
а) точка, в якій лінія регресії перетинає вісь У;
б) зв'язок між незалежною і залежною змінними;
в) точка, в якій лінія регресії перетинає вісь Х;
г) завжди дорівнює 1.
11.12 Критерій Стьюдента використовується для:
а) перевірки на значущість коефіцієнтів регресії;
б) визначення тісноти зв’язку між змінними, що входять до моделі;
в) визначення значущості факторів, які є в моделі;
г) встановлення достовірності даних, що використовуються для розрахунку економетричної моделі.
11.13 Критерії Фішера застосовуються для:
а) перевірки адекватності параметрів економетричної моделі;
б) встановлення тісноти зв’язку між змінними;
в) обґрунтування форми зв’язку між залежними і незалежними змінними;
г) перевірки параметрів моделі стосовно їх суттєвості та значущості