- •Эйлеровы и гамильтоновы графы
- •Сети, потоки в сетях. Теорема Форда – Фалкерсона
- •Алгоритм выделения компонент сильной связности
- •Алгоритм фронта волны.
- •Минимальный путь в нагруженном ориентированном графе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон).
- •Деревья
Алгоритм выделения компонент сильной связности
1.
Присваиваем p=1
(p
− количество
компонент связности),
![]() .
.
2. Включаем в множество вершин Vp компоненты сильной связности Gp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы AGp возьмем подматрицу матрицы AG, состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем p=p+1 и переходим к п. 2.
Пример
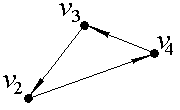
Выделим компоненты связности ориентированного графа, изображенного на рис. 1. В данной задаче количество вершин n=5.
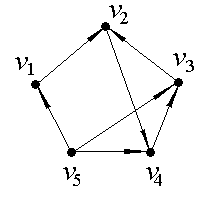
Рис. 1.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
 .
.
Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения:
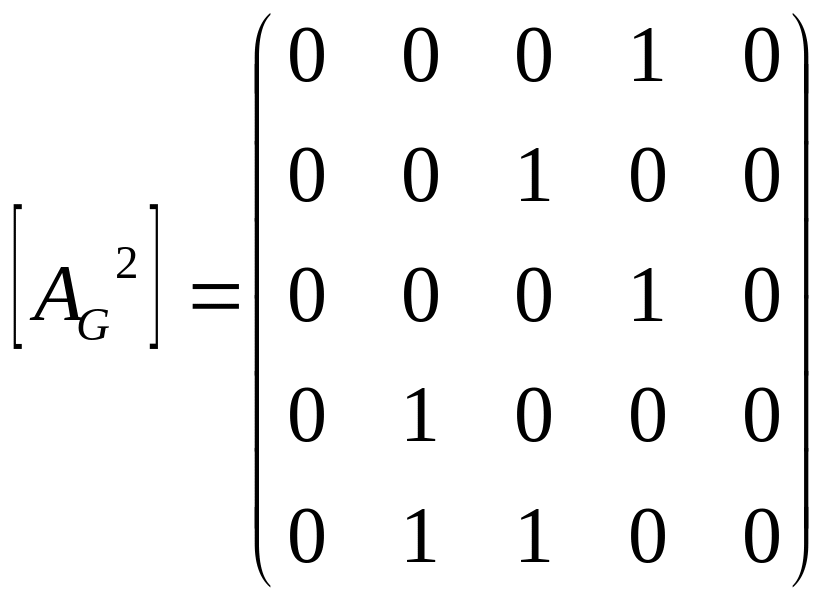 ,
,
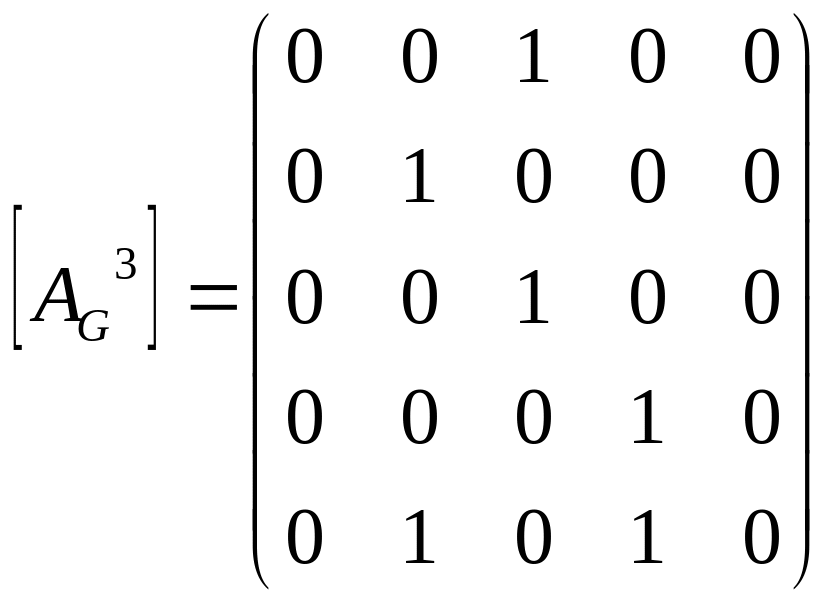 ,
,
 ,
,
Следовательно,

 .
.
Таким образом, матрица сильной связности, будет следующей:
 .
.
Присваиваем
p=1
и составляем множество вершин первой
компоненты сильной связности G1:
это те вершины, которым соответствуют
единицы в первой строке матрицы SG.
Таким образом, первая компонента сильной
связности состоит из одной вершины
![]() .
.
Вычеркиваем из матрицы S1 строку и столбец, соответствующие вершине v1, чтобы получить матрицу S2:
 .
.
Присваиваем
p=2.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы S2,
то есть
![]() .
Составляем матрицу смежности для
компоненты сильной связности G
.
Составляем матрицу смежности для
компоненты сильной связности G![]() исходного графа G
− в ее
качестве возьмем подматрицу матрицы
AG,
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
V2:
исходного графа G
− в ее
качестве возьмем подматрицу матрицы
AG,
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
V2:
 .
.
Вычеркиваем из матрицы S2 строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3, которая состоит из одного элемента:
![]()
и
присваиваем p=3.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины
![]() .
.
Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
G1:
|
G2:
|
G3:
|
Алгоритм фронта волны.
Определение:![]() -
образ
вершины
-
образ
вершины![]() - множество вершин, в которые исходят
дуги из данной вершины.
- множество вершин, в которые исходят
дуги из данной вершины.
Пусть
необходимо найти минимальный путь из
вершины
в вершину
![]() .
.
Выписываются все вершины с 1 по n. Вершина помечается индексом 0.
Находится первый фронт волны
 как множество вершин образа вершины
.
как множество вершин образа вершины
.
![]() (3.17)
(3.17)
Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.
Вводится счетчик шагов (фронтов волны)
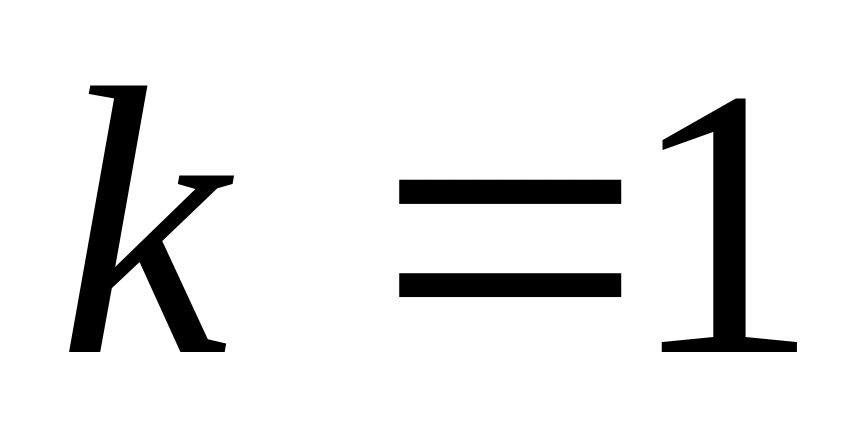 .
.Если
 или
или
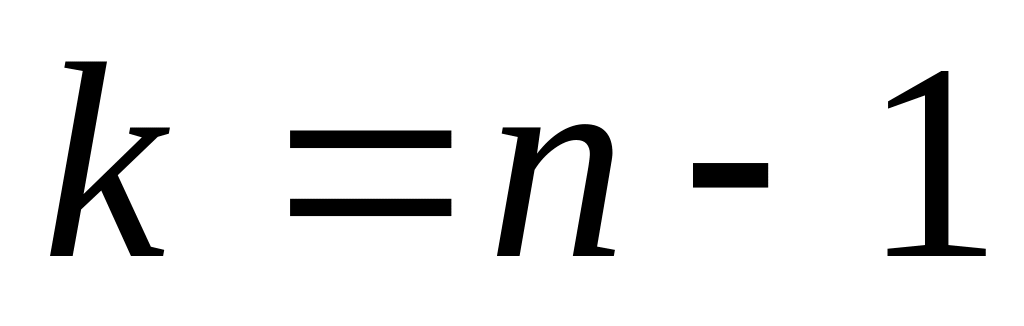 ,
то вершина
недостижима из вершины, и работа
алгоритма на этом заканчивается. В
противном смысле переходим к пункту
6.
,
то вершина
недостижима из вершины, и работа
алгоритма на этом заканчивается. В
противном смысле переходим к пункту
6.Если
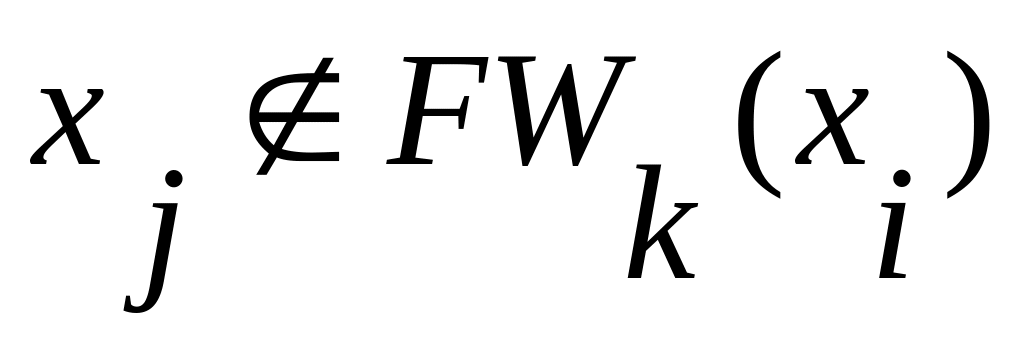 ,
то переходим к пункту 8. В противном
случае существует путь из вершины
в вершину
длиной в
,
то переходим к пункту 8. В противном
случае существует путь из вершины
в вершину
длиной в
 единиц, и этот путь минимальный:
единиц, и этот путь минимальный:
![]()
Находятся промежуточные вершины
 z
по правилу:
z
по правилу:
![]()
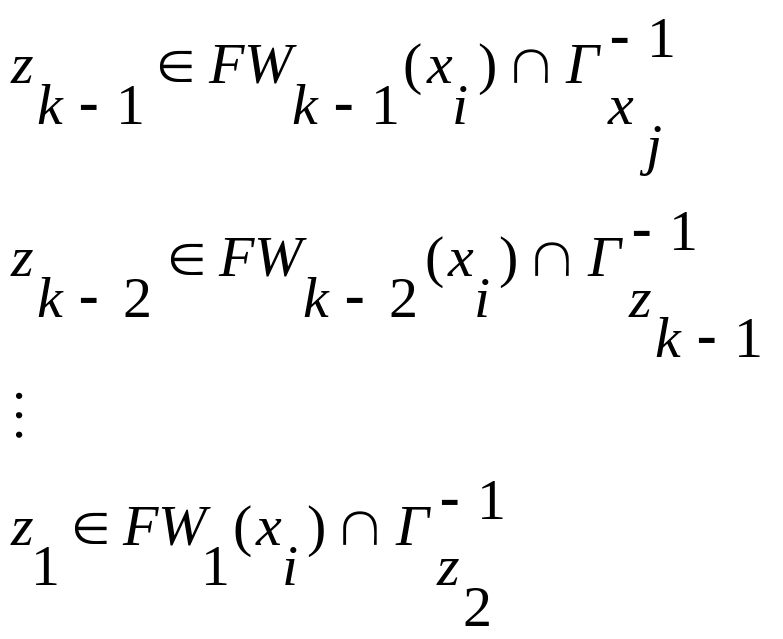 , (3.18)
, (3.18)
где
![]() -
прообраз вершины
-
прообраз вершины
![]() - множество вершин, из которых
заходят дуги в вершину
- множество вершин, из которых
заходят дуги в вершину
Определяется
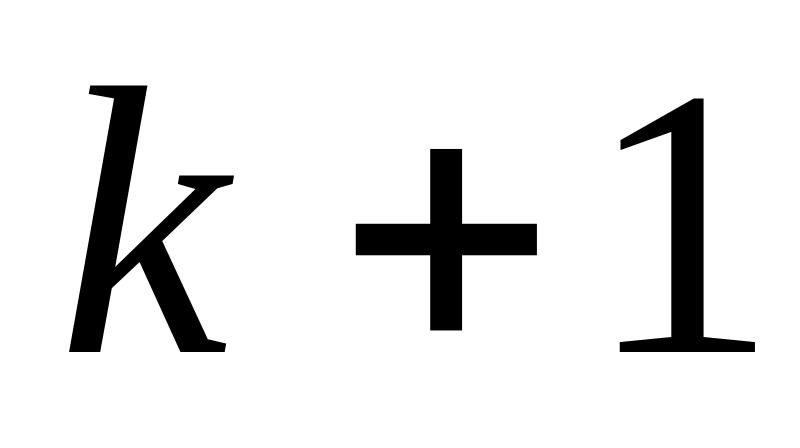 фронт волны как все непомеченные
вершины, принадлежащие образу вершин
- го фронта волны. Помечаются индексом
вершины
фронта волны. Далее осуществляется
переход к пункту 5.
фронт волны как все непомеченные
вершины, принадлежащие образу вершин
- го фронта волны. Помечаются индексом
вершины
фронта волны. Далее осуществляется
переход к пункту 5.
ПРИМЕР
Пусть задан граф матрицей смежности:
-
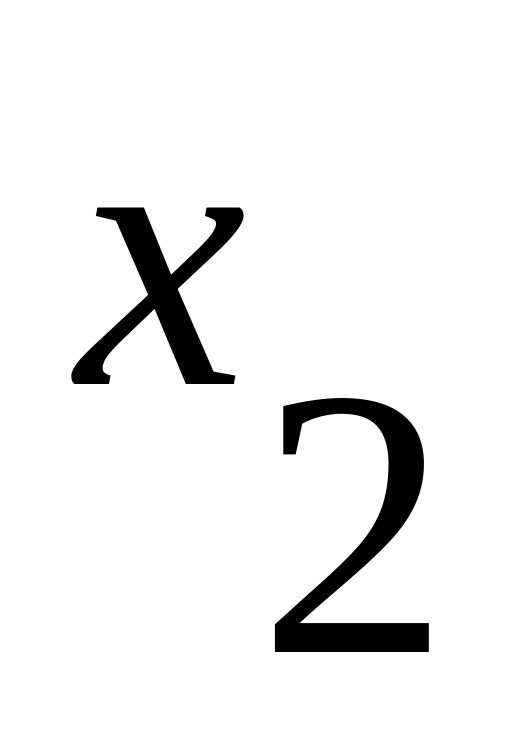
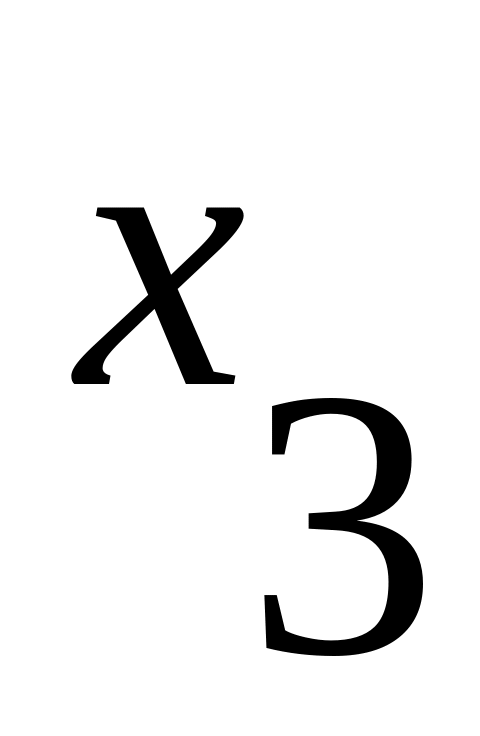
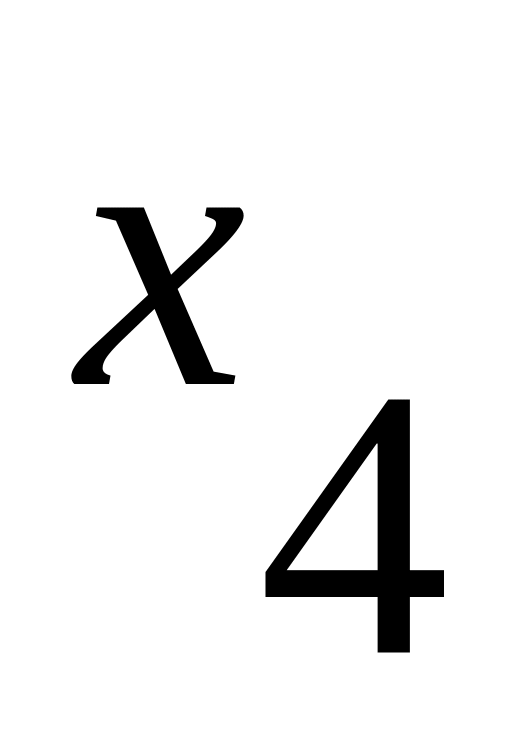



1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Необходимо найти минимальный путь из вершины в вершину (по алгоритму «фронта волны»).
Выпишем все вершины. Вершина помечается индексом «0»
0
![]()
Находится первый фронт волны:
![]()
Все вершины, принадлежащие первому фронту волны, помечаются индексом «1».
0 1 1
Так как
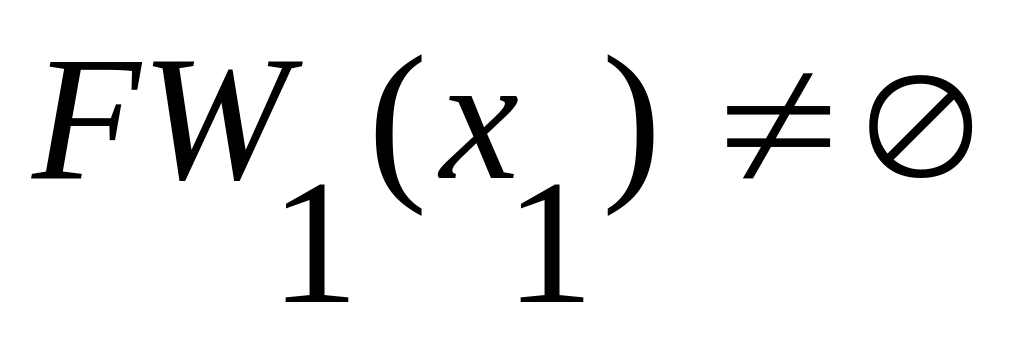 ,
,
 и
и
 ,
то определяем второй фронт волны:
,
то определяем второй фронт волны:
![]()
Все вершины, принадлежащие второму фронту волны, помечаются индексом «2».
0 2 2 1 1
Так как
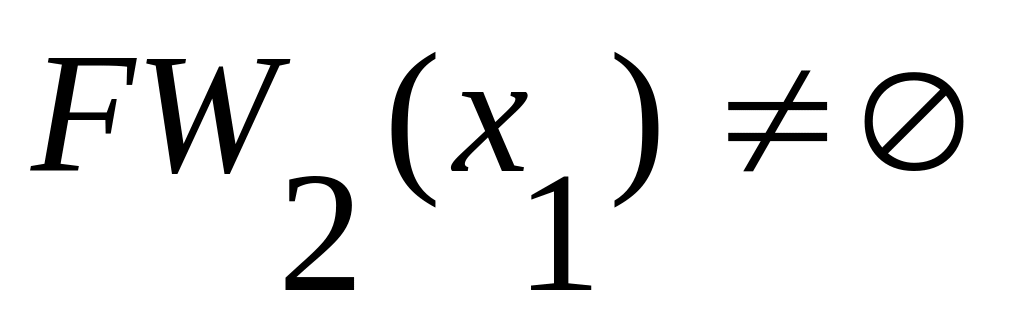 ,
,
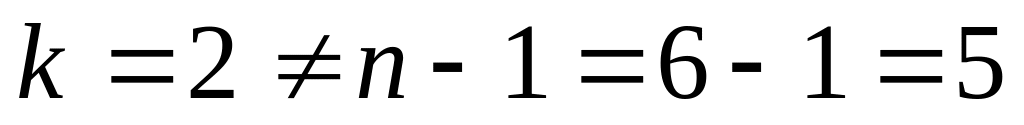 и
и
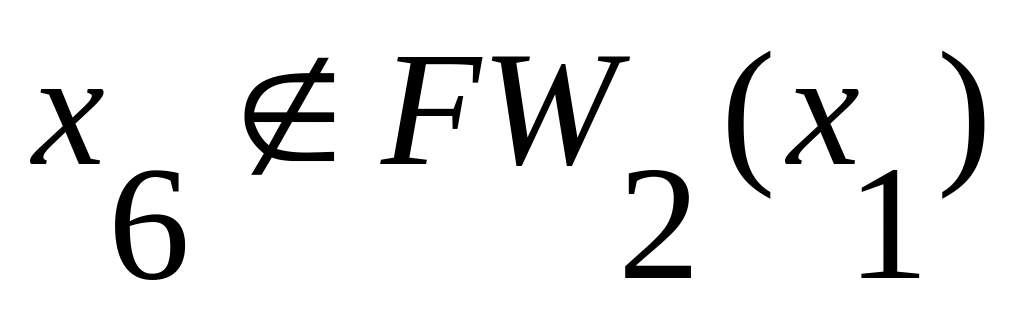 ,
то определяем третий фронт волны:
,
то определяем третий фронт волны:
![]()
Так как
 ,
то существует путь из вершины
в вершину
длиной 3 единицы:
,
то существует путь из вершины
в вершину
длиной 3 единицы:
![]()
Находятся промежуточные вершины
 :
:
![]()
Выберем
![]()
![]()
Выберем
![]()
Таким образом, минимальный путь из вершины в вершину имеет вид:
![]()