Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский государственный национальный исследовательский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

!Итог методичка С_К.doc

Скачиваний:

Добавлен:

24.08.2019

Размер:

5.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

3. Функциональные ряды

Пример 20. Найти область сходимости ряда .

Решение. Данный ряд представляет собой обобщенный гармонический ряд , который сходится, и притом абсолютно, при и расходится при . Область сходимости ряда определяется двойным неравенством .

Пример 21. Найти область сходимости ряда .

Решение. Так как не входит в область определения функций – членов ряда, то можно считать . Применим признак Даламбера. И так как этот признак применим лишь к рядам с положительными членами, то исследуем ряд сразу на абсолютную сходимость. Так как , то

Отсюда вытекает, что ряд сходится, и притом абсолютно, при . При ряд расходится, как не удовлетворяющий необходимому признаку сходимости. Если , то признак Даламбера ответа о сходимости ряда не дает и, следовательно, при ряд нужно исследовать особо. При получается гармонический ряд , он расходится; при - сходящийся ряд Лейбница . Таким образом, область сходимости данного ряда характеризуется неравенством .

Пример 22. Найти область сходимости ряда .

Решение. Ряд имеет вид , то есть является степенным рядом. Здесь . Следовательно, радиус сходимости может быть определен по формуле

или по формуле

Интервал сходимости характеризуется неравенством . Исследуем сходимость ряда в граничных точках этого интервала. При степенной ряд принимает вид

Оба ряда расходятся, так как не удовлетворяют необходимому признаку сходимости. Следовательно, область сходимости данного степенного ряда совпадает с его интервалом сходимости: .

Пример 23. Найти область сходимости степенного ряда .

Решение. В развернутом виде ряд записывается так:

и ясно, что бесконечное множество его коэффициентов равно нулю: . Следовательно, применение формул из предыдущего примера недопустимо. Поэтому для нахождения области сходимости применим непосредственно признак Коши (возможно применение и признака Даламбера):

Итак, исследуемый ряд сходится в интервале . В граничных точках этого интервала ряд расходится, так как при он не удовлетворяет необходимому признаку сходимости ряда. Значит область сходимости – интервал .

В заключение заметим, что более эффективным решением этого примера является применение формулы

Пример 24. Для ряда построить мажорирующий ряд и установить равномерную сходимость на любом отрезке.

Решение. Для всех значений справедливо неравенство . Это значит, что ряд с общим членом мажорирует данный функциональный ряд. Так как ряд - сходящийся, то исходный функциональный ряд, по принципу Вейерштрасса, сходится на любом отрезке.

Пример 25. Исследовать на равномерную сходимость ряд .

Решение. Данный ряд сходится в промежутке , как знакочередующийся по признаку Лейбница. В этом промежутке он сходится лишь условно и поэтому признак Вейерштрасса неприменим. Однако, пользуясь известной оценкой остатка знакочередующегося ряда , легко получить неравенства

Каково бы ни было , найдется номер такой, что для всех будет справедливо неравенство .

Тогда и подавно при и всех x промежутка выполняется неравенство . Это и свидетельствует о равномерной сходимости данного ряда в упомянутом промежутке.

В решении этого примера - целая часть числа (наибольшее целое число, не превосходящее ).

Пример 26. Доказать равномерную сходимость ряда на отрезке [0,1].

Решение. Будем рассматривать данный ряд, как ряд вида

, где , .

Воспользуемся признаком Абеля. Ряд сходится равномерно в промежутке (это доказано в примере 25). Следовательно, он сходится равномерно и на отрезке [0,1].

Из курса математического анализа известно, что последовательность для любого x > 0 монотонно возрастает при и имеет пределом число . Поэтому функции ограничены на отрезке [0,1].числом и при каждом образуют монотонную (возрастающую) последовательность. Отсюда следует, что, по признаку Абеля, данный ряд сходится на отрезке [0,1] равномерно.

Пример 27. Доказать равномерную сходимость ряда на любом отрезке, не содержащем точек вида .

Решение. Исследуем ряд на равномерную сходимость с помощью признака Дирихле. Будем рассматривать его как ряд вида , где .

Последовательность монотонно сходится к нулю, и поэтому первое условие признака Дирихле выполнено. Проверим выполнимость второго условия. Известно, что для частичных сумм ряда справедливо неравенство . В точках , а на любом отрезке, не содержащем этих точек, функция непрерывна, и, следовательно, ограничена. Поэтому существует число M > 0 такое, что на каждом из этих отрезков.

Вывод: так как последовательность монотонно сходится к нулю, а частичные суммы ряда ограничены на любом отрезке, не содержащем точек , одним и тем же числом, то данный функциональный ряд, по признаку Дирихле, сходится равномерно на любом отрезке.

4. Степенные ряды

Пример 28. Разложить функцию в ряд Тейлора по степеням .

Решение. Применим прием непосредственного разложения.

а) Составим для данной функции ряд Тейлора. С этой целью найдем сначала числовые значения производных всех порядков функции в точке :

Подставляя теперь найденные значения производных в формулу ряда Тейлора при , получим ряд Тейлора для функции по степеням :

б) Находим область сходимости полученного ряда. Так как

то ряд сходится для всех значений .

в) Выясним, для каких значений найденное разложение сходится к функции . С этой целью заметим, что производные всех порядков данной функции на любом отрезке ввиду справедливости неравенства ограничены одним и тем же числом :

Отсюда следует, что найденное разложение сходится к функции при всех значениях :

Пример 29. Пользуясь разложениями элементарных функций, разложить в ряд Маклорена функцию .

Решение. Полагаем и используем табличное разложение в ряд Маклорена функции . Тогда

Так как разложение в ряд функции имеет место для всех , то и разложение в ряд данной функции имеет место для всех .

Пример 30. Разложить в ряд по степеням функцию и указать область сходимости полученного разложения к функции .

Решение. Так как

где , то воспользуемся табличным разложением функции :

Полученное разложение верно для всех значений , удовлетворяющих неравенству . Следовательно, для нахождения области сходимости найденного ряда к данной функции нужно решить неравенство . Решение приводит к следующему результату: . Этими неравенствами и характеризуется область сходимости ряда к данной функции.

Пример 31. Найти сумму ряда .

Решение. Интервал сходимости данного ряда находится стандартным способом и имеет вид (-1,1). На основании теоремы о дифференцировании степенных рядов его можно дифференцировать в каждой точке интервала (-1,1). Выполним дифференцирование:

Суммируя полученную бесконечно убывающую при прогрессию, находим , откуда

Постоянную можно вычислить, зная, что при и, следовательно, , откуда . Таким образом, сумма данного ряда . Данный ряд сходится к своей сумме для .

Заметим, что данный ряд расходится в граничной точке и сходится, по признаку Лейбница, в граничной точке . По второй теореме Абеля, в случае сходимости степенного ряда в граничной точке имеем . В нашем случае , , и, следовательно,

Таким образом, область сходимости данного ряда к функции характеризуется двойным неравенством .

Пример 32. Найти сумму ряда .

Решение. Положим и найдем сумму степенного ряда , сходящегося для (что нетрудно установить с помощью признака Даламбера). Интегрируя равенство = на отрезке (что возможно на основании теоремы об интегрировании степенных рядов) и затем дифференцируя полученное равенство по , будем иметь

; ,

но , поэтому

= .

Разложение имеет место для всех значений , удовлетворяющих неравенству , то есть для , откуда и . Эти неравенства и определяют область сходимости данного ряда к сумме .

Пример 33. Найти сумму ряда .

Решение. Составим вспомогательный степенной ряд и обозначим его сумму через . Нужно найти . Для этого продифференцируем обе части равенства = по (это возможно на основании теоремы о дифференцировании степенных рядов) и вычислим сумму ряда производных:

Проинтегрируем теперь обе части равенства на отрезке :

;

тогда

5.Приложения рядов

Пример 34. Вычислить с точностью до .

Решение. Перепишем данное выражение в виде

Подставим в биноминальный ряд

и . Получим знакочередующийся ряд

=4 .

Нетрудно показать, что этот ряд является рядом Лейбница (удовлетворяет условиям теоремы Лейбница). Согласно теореме Лейбница погрешность, допускаемая при отбрасывании членов ряда, по абсолютной величине не превышает модуля первого отброшенного члена. Так как , то для достижения требуемой точности достаточно взять первые два члена ряда

= .

Пример 35. Вычислить с точностью до .

Решение. Для вычисления логарифмов чисел можно пользоваться рядом

, .

Ошибка, получаемая при замене суммы ряда суммой его первых членов, может быть оценена с помощью формулы

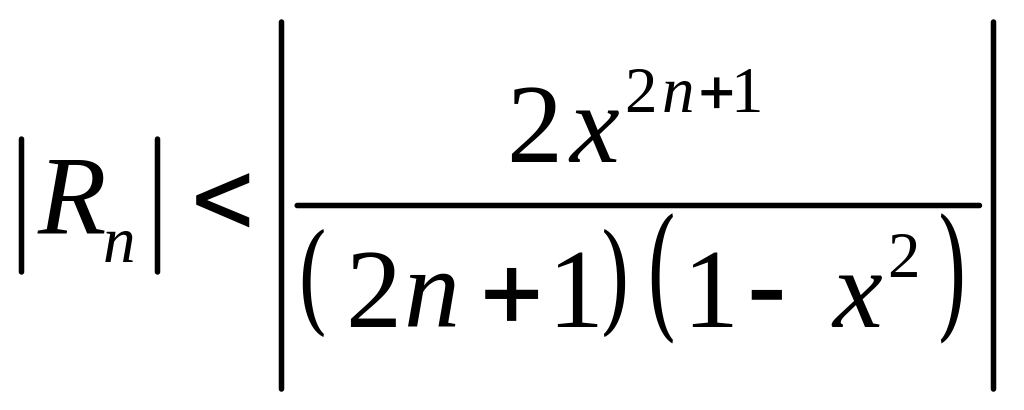Положим , тогда и, следовательно,

Заданную точность обеспечивают четыре члена, так как для оценки погрешности выполняется неравенство ( и )

Таким образом, с точностью до

Пример 35. Найти с точностью определенный интеграл .

Решение. Первообразная функции не выражается в элементарных функциях, поэтому нельзя применить формулу Ньютона-Лейбница. Вычислим данный интеграл приближенно с помощью разложения подинтегральной функции в степенной ряд. Умножим обе части разложения

на , получим

= .

Проинтегрируем полученный ряд в указанных пределах

Полученный ряд удовлетворяет условиям теоремы Лейбница. Так как 5-й член по абсолютной величине не превышает , то для получения указанной точности берем первые 4 члена ряда:

Пример 36. Найти первые три (отличные от нуля) члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Решение. Будем искать решение уравнения в виде ряда Маклорена

предполагая при этом, что этот ряд сходится на всей числовой оси и его можно дифференцировать в любой точке. Первый коэффициент найдем из начального условия:

. Значение находим, подставив =1 и в исходное уравнение:

Получим .

Следующие коэффициенты найдем последовательным дифференцированием исходного уравнения и подстановкой :

; ,

; .

Искомое решение имеет вид:

Контрольные задания к теме 6.

Числовые и функциональные ряды.

Задание 1: Исследовать сходимость ряда по признаку сравнения.

Задание 2: Исследовать сходимость ряда.

Задание 3: Исследовать на абсолютную и условную сходимость ряд.

Задание 4: Исследовать сходимость (абсолютную и условную) ряда.

Задание 5: Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке.

Задание 6: Доказать равномерную на множестве А сходимость ряда.

Задание 7: Найти область сходимости ряда.

Задание 8: Данную функцию разложить в ряд Маклорена, используя известные разложения в ряд функций:

Задание 9: Разложить в ряд Тейлора указанную функцию в окрестности точки и найти его область сходимости.

Задание 10: Вычислить с точностью до .

Задание 11: Вычислить с точностью до определенный интеграл.

Задание 12: Методом последовательного дифференцирования найти первые членов разложения в степенной ряд решения дифференциального уравнения при указанных начальных условиях.