Курсовая работа Частица в потенциальной яме со стенками бесконечной длины / курсач

Государственный комитет РФ по высшему образованию

Санкт-Петербургский Государственный Электротехнический

Университет им. В.И. Ульянова (Ленина)

Кафедра ФЭОП

Курсовая работа по Квантовой механике на тему:

Частица в одномерной бесконечной потенциальной яме

Руководитель: Варнашев К.Б.

Студент группы 2211: Тимофеев Ю.В.

Санкт-Петербург

2004 г.

Содержание

	Содержание…………………………………………………………………………………………………………………………………………	2
1	Задание на курсовую работу………………………………………………………………………………………………	3
2	Нахождение энергетического спектра электрона в яме……………………………………………………………………………………………………………………………………………………………	4
3	Нахождение волновых функций……………………………………………………………………………………………	10
4	Расчет вероятности нахождения электрона в центральной части ямы……………………………………………………………………………………………………………………………………………………………	15

1. Задание на курсовую работу

Вариант №4б

Найти энергии и волновые функции первых трех стационарных состояний электрона в потенциальной яме следующего вида:

, при ;

, при ;

, при ;

Построить графики волновых функций этих состояний. Вычислить вероятность обнаружения электрона в центральной части ямы (т.е. в интервале ) для указанных состояний.

2. Нахождение энергетического спектра электрона в яме

Потенциальная яма симметрична относительно начала отсчета, следовательно, в дальнейшем можно рассматривать только две области:

I -

II -

Запишем уравнения Шредингера для областей:

Запишем уравнения в приведенном виде (умножим оба уравнения на ):

, где ;

, где ; для

, где ; для

Случай с низкими энергиями ()

Общее решение этих уравнений, с учетом того, что в точке функция должна обращаться в 0:

Граничные условия: ,

Вследствие симметрии потенциала, решения могут быть четные и нечетные. Рассмотрим оба случая.

1. Четные состояния

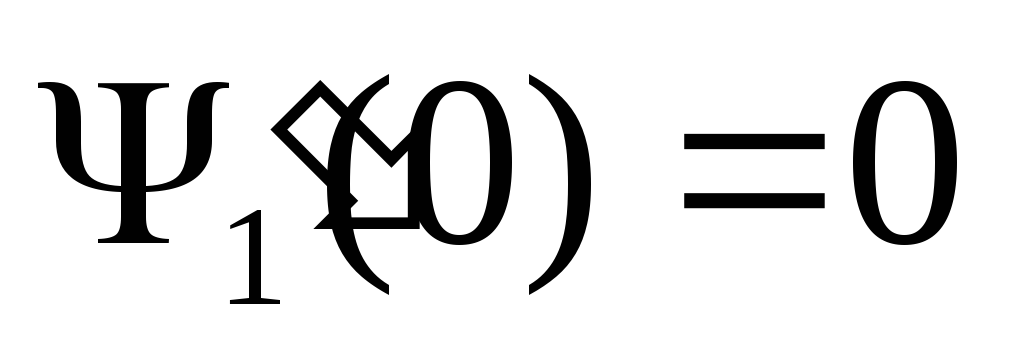
Для четных состояний общее решение уравнений Шредингера будет в виде:

Из граничных условий следует:

Разделив одно уравнение на другое получим:

(1)

Рассмотрим величину:

Введем новую переменную , тогда:

,

где - минимальная энергия частицы.

С учетом этих замен (1) перепишется в виде (умножив обе части уравнения на ):

Получили трансцендентное уравнение, решение которого можно получить графически (см. рис2).

2. Нечетные состояния

Для четных состояний общее решение уравнений Шредингера будет в виде:

Из граничных условий следует:

Разделив одно уравнение на другое получим:

(2)

С учетом замен (2) перепишется в виде (умножив обе части уравнения на ):

Получили трансцендентное уравнение, решение которого можно получить графически (см. рис2).

где

Чтобы избежать комплексных значений необходимо наложить ограничение .

С учетом наложенных ограничений решение трансцендентных уравнений:

;

;

Для нахождения рассмотрим случай с

Случай с высокими энергиями ()

Общее решение этих уравнений, с учетом того, что в точке функция должна обращаться в 0:

Граничные условия: ,

Вследствие симметрии потенциала, решения могут быть четные и нечетные. Рассмотрим оба случая.

3. Четные состояния

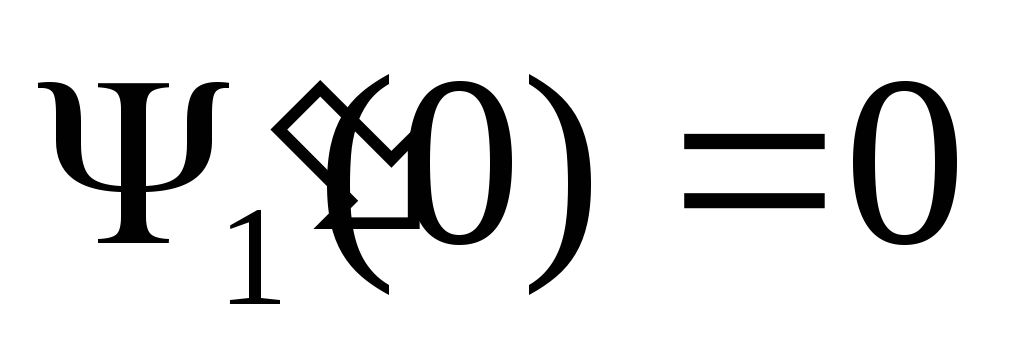
Для четных состояний общее решение уравнений Шредингера будет в виде:

Из граничных условий следует:

Разделив одно уравнение на другое получим:

(3)

Рассмотрим величину:

Введем новую переменную , тогда:

,

где - минимальная энергия частицы.

С учетом этих замен (3) перепишется в виде (умножив обе части уравнения на ):

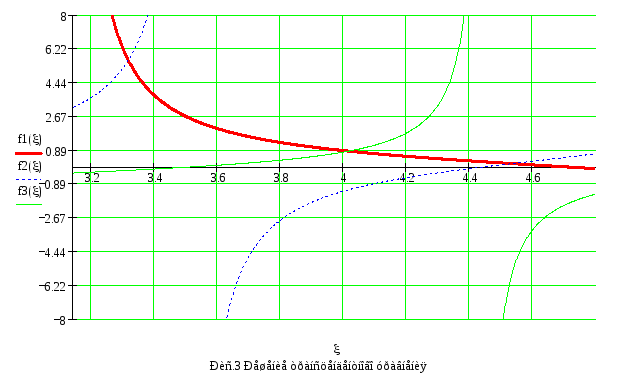
Получили трансцендентное уравнение, решение которого можно получить графически (см. рис3).

4. Нечетные состояния

Для четных состояний общее решение уравнений Шредингера будет в виде:

Из граничных условий следует:

Разделив одно уравнение на другое получим:

(4)

С учетом замен (4) перепишется в виде (умножив обе части уравнения на ):

Получили трансцендентное уравнение, решение которого можно получить графически (см. рис3).

где

Чтобы избежать комплексных значений необходимо наложить ограничение

С учетом наложенных ограничений решение трансцендентных уравнений:

;

Для нахождения энергетического спектра воспользуемся формулой:

Подставляя полученные значения , получаем:

; ; ;

При , тогда энергии состояния будут равны:

;

;

;

3. Нахождение волновых функций

; ; ;

Найдем неизвестные константы A, B, C и D. Причем, условимся обозначать:

- константы для первого энергетического уровня;

- константы для второго энергетического уровня;

- константы для третьего энергетического уровня;

Волновая функция первого энергетического уровня

Из выражения для граничных условий (четные) найдем связь с :

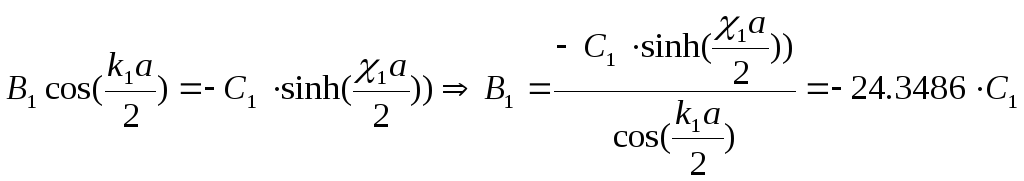
Получили систему:

Константу можно найти из условия нормировки:

Окончательно получаем выражения для волновой функции первого энергетического состояния (график функции см. на рис.4):

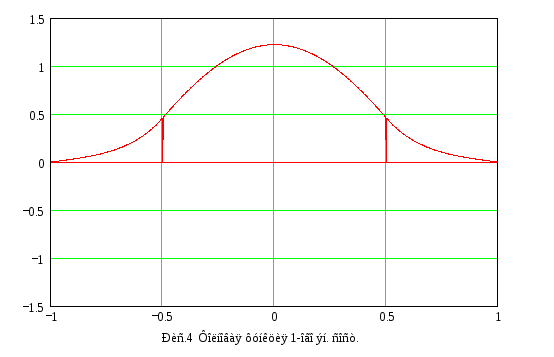
Волновая функция второго энергетического уровня

Из выражения для граничных условий (нечетные) найдем связь с :

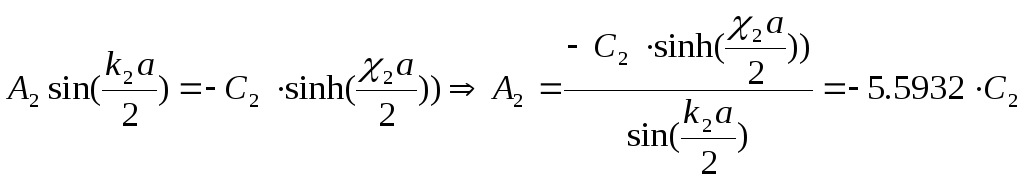
Получили систему:

Константу можно найти из условия нормировки:

Окончательно получаем выражения для волновой функции второго энергетического состояния (график функции при см. на рис.5):

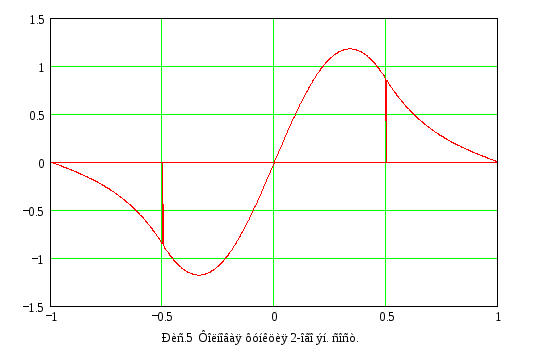
Волновая функция третьего энергетического уровня

Из выражения для граничных условий (четные) найдем связь с :

Получили систему:

Константу можно найти из условия нормировки:

Окончательно получаем выражения для волновой функции третьего энергетического состояния (график функции при см. на рис.6):

3. Расчет вероятности нахождения электрона в центральной части ямы (т.е. при ) для первых трех состояний

Первое энергетическое состояние:

Второе энергетическое состояние:

Третье энергетическое состояние:

15