11кл. Інтеграл Варіант 1
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = sin 4x
а)
б)
в) 4cos
4x
+ C г)
–cos
4x
+C
2.
Обчисліть
А) 9; Б) 3; В) 26; Г) 27; Д) 6
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
у = х2
А
4х2 + С
2
Б
3
у = 8 х
В
3х2 + С
4
Г
8 ln x + C
Д
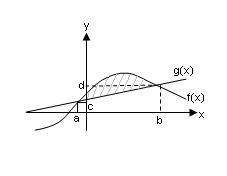
4. Площа фігури, обмеженої
л
ініями
y
= f(x)
и y
= g(x),
обчислюється за формулою:
а)
б)
в)
г)
д)
II частина (по 2б)
5.
Обчисліть: а)
6.
Укажіть первісну для функції
,
графік якої проходить через точку
III частина ( 3б)
7. Знайдіть площу фігури, обмеженої лініями у = 4 – х2 і у = 2 – х.
11кл. Інтеграл Варіант 2
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = соs 3x
а)
б)
sin
3x
+ C
в)
г)
-3sin
3x
+ C д)
3sin
3x
+ C
2.
Обчисліть
А) 24; Б) 16; В) 4; Г) 8; Д) 6
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
4х2 + С
2
у = х2
Б
3
у = 2 х
В
2 ln x + C
4
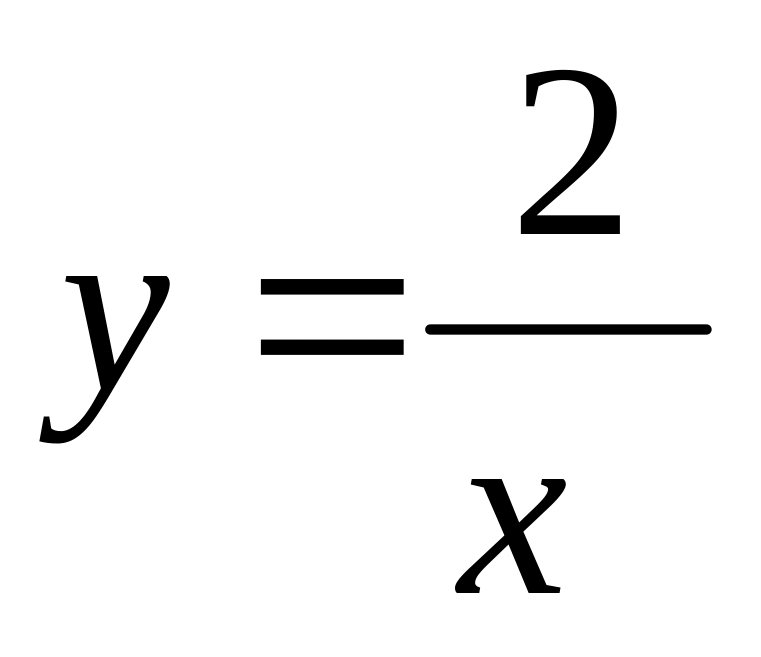
Г
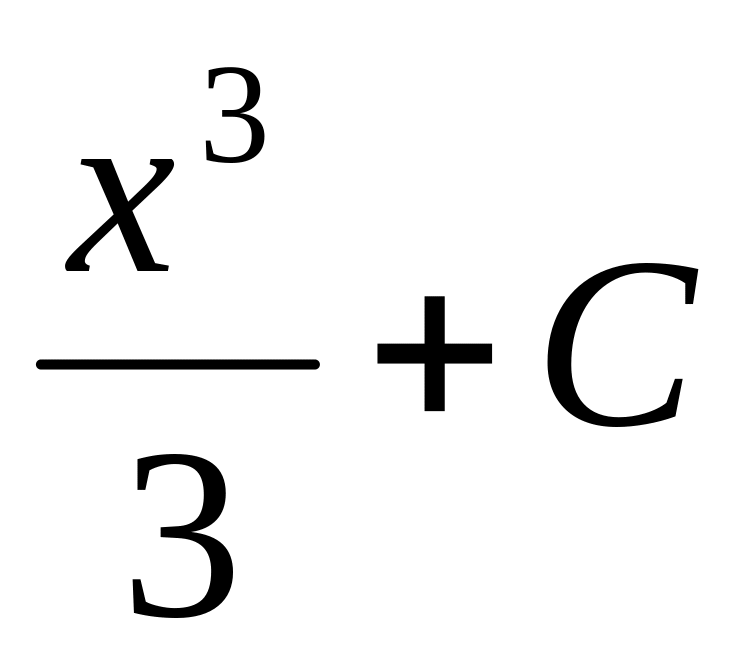
Д
х2 + С
4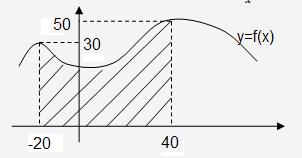
.
Площа
фігури, зображеної
на малюнку, обчислюється за формулою:
а)
б)
в)
г)
д)
інша
відповідь.
II частина (по 2б)
5.
Обчисліть: а)
6.
Укажіть первісну для функції
,
графік якої проходить через точку
III частина ( 3б)
7. Знайдіть площу фігури, обмеженої лініями у = 6 – х2 і у = х + 4.
.
11кл. Інтеграл Варіант 3
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = sin 9x
а)
б)
в) -9cos
9x
+ C
г) –cos
9x
+C
д) 9cos
9x
+ C
2.
Обчисліть
а) 4; б) 6; в) 8; г) -4; д) -6
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
2
Б
3
у = 5 х
В
3х2 + С
4
у = х5
Г
5 ln x + C
Д
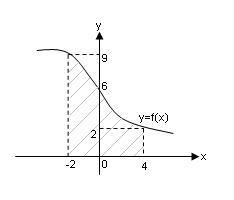
4. Площа фігури, обмеженої
лініями y = f(x) и y = g(x),
обчислюється за формулою:
а)
б)
в)
г)
д)
інша відповідь
II частина (по 2б)
5.
Обчисліть: а)
;
6.
Укажіть первісну для функції
,
графік якої проходить через точку
III частина ( 3б)
7. Знайдіть площу фігури, обмеженої лініями у = 5 – х2 і у = 3 – х.
11кл. Інтеграл Варіант 4
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = соs 5x
а)
б)
sin
5x
+ C
в)
5sin
5x
+ C г)
-5sin
5x
+ C д)
2.
Обчисліть
А)
;
Б) 1;
В)
;
Г)
; Д)
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
4х2 + С
2
у = х2
Б
3
у = 2 х
В
2 ln x + C
4
Г
Д
х2 + С
4. Площа фігури, зображеної
на малюнку, обчислюється за формулою:
а)
б)
в)
г)
д)
.
II частина (по 2б)
5. Обчисліть: а) ;
6. Укажіть первісну для функції , графік якої проходить через точку
III частина ( 3б)
7. Знайдіть площу фігури, обмеженої лініями у = 6 – х2 і у = х + 4.
11кл. Інтеграл Варіант 5
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = sin 4x
а) б) в) 4cos 4x + C г) –cos 4x +C д) інша відповідь
2.
Обчисліть
dx
а)5xlnx
+ С;
б)
5xln5
+ С;
в)
;
г) 
;
д)
інша
відповідь
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
у = х2
А
4х2 + С
2
Б
3
у = 8 х
В
3х2 + С
4
Г
8 ln x + C
Д
4. Площа фігури, обмеженої
л ініями y = f(x) и y = g(x),
обчислюється за формулою:
а)
б)
в)
г) д)
II частина (по 2б)
5.
Обчисліть: а)
; б)
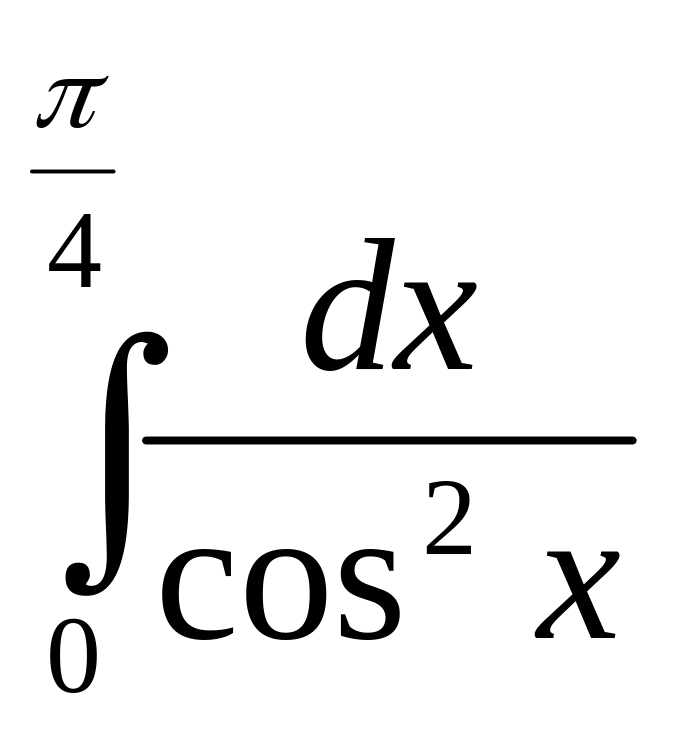
6. Укажіть первісну для функції , графік якої проходить через точку
III частина ( 3б)
7. Знайдіть площу фігури, обмежену параболою y=6x-3x2, дотичною, яка проведена до цієї параболи в точці з абсцисою х0=2 і віссю ординат.
11кл. Інтеграл Варіант 6
I частина (по 1б)
1. Укажіть загальний вигляд первісної для функції f(x) = соs 3x
а) б) sin 3x + C в) г) -3sin 3x + C д) 3sin 3x + C
2.
Обчисліть
а)
7xlnx+C;
б) 
+C;
в) 
+C;
г) 7xln7+C;
д) інша відповідь
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
4х2 + С
2
у = х2
Б
3
у = 2 х
В
2 ln x + C
4
Г
Д
х2 + С
4 . Площа фігури, зображеної
на малюнку, обчислюється за формулою:
а)
б)
в)
г) д) інша відповідь.
II частина (по 2б)
5
Обчисліть: а)
; б)
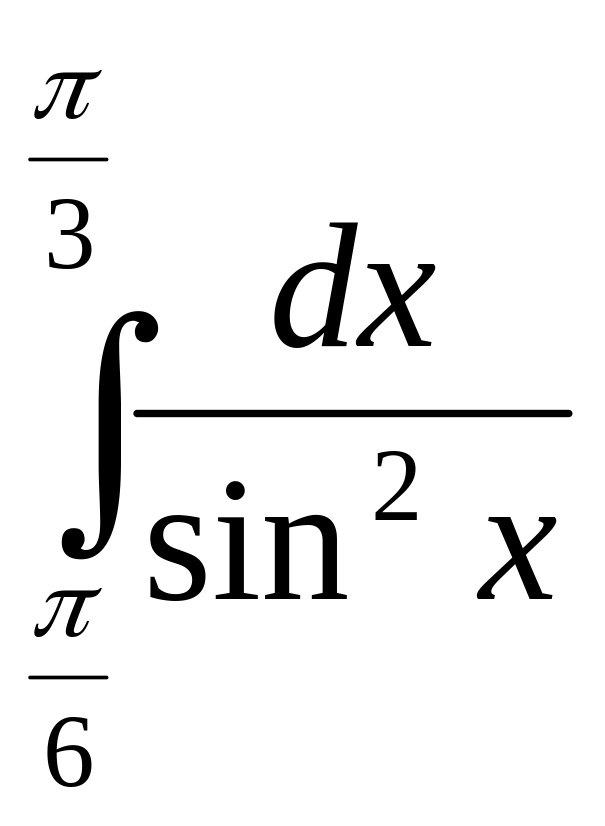
6. Укажіть первісну для функції , графік якої проходить через точку
III частина ( 3б)
7.
Знайдіть
площу фігури, обмеженої лініями y=sinx,
y=cosx,
x=
,
x=
.
..11кл. Інтеграл Варіант 7
I частина (по 1б)
1.
Укажіть
загальний вигляд первісної для функції
f(x)
= f(x)=x4+
а)
б)
4x3+
ctgx
в) 
+
ctgx+C г)
4x3+
tgx
+С
д) інша відповідь.
2.
Обчисліть
а)
+C;
б)
+C;
в)
+C;
г)
+C; д)
інша
відповідь
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
2
Б
3
у = 5 х
В
3х2 + С
4
у = х5
Г
5 ln x + C
Д
4. Площа фігури, обмеженої
лініями y = f(x) и y = g(x),
обчислюється за формулою:
а)
б)
в)
г) д) інша відповідь
II частина (по 2б)
5.
Обчисліть: а)
; б)
6. Укажіть первісну для функції , графік якої проходить через точку
III частина ( 3б)
7. При
якому
значенні
параметра а пряма х=а ділить
площу
фігури,
обмеженої
лінією y=
и прямими
y=0,
x=4,
x=9,
навпіл?
11кл. Інтеграл Варіант 8
I частина (по 1б)
1.
Укажіть
загальний вигляд первісної для функції
f(x)
= x3-
а) 
б)
+ctgx+C
в)
3x2-tgx+C г)
3x2+2cosx+C д)
інша відповідь.
2.
Обчисліть
а)
;
б)
; в)
; г)
; д)
) інша
відповідь
3. (За кожну відповідь по 0,5 б.) Установіть відповідність між функціями (1-4) та їхніми первісними (А-Д)
-
1
А
4х2 + С
2
у = х2
Б
3
у = 2 х
В
2 ln x + C
4
Г
Д
х2 + С
4. Площа фігури, зображеної
на малюнку, обчислюється за формулою:
а)
б)
в)
г) д) .