Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

« ПЕРМСКИЙ ГОСУДАРСТВЕНЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

КАФЕДРА МАТЕМАТИЧЕСКОГО АНАЛИЗА

Курсовая работа

Интегралы зависящие от параметра

Работу выполнил:

студент 132 группы

математического факультета

Зенков Яков Алексеевич

Проверила: Скорнякова Анна Юрьевна.

Пермь 2009 г.

Содержание.

1. СОБСТВЕННЫЕ и несобственные ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА

2.1. Определение сообственных интегралов, зависящих от параметра.

2.2. О допустимости предельного перехода по параметру под знаком

2.3. Определение равномерной сходимости несобственных интегралов.

2.4. О непрерывности интеграла как функции параметра.

2. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ.

3.1. Интеграл Эйлера первого рода (Бета-функция).

3.2. Интеграл Эйлера второго рода (Гамма-функция).

Введение

Данная тема актуальна в ВУЗах, так как тема интегралы зависящие от параметра в курсе математического анализа не изучается. Эта исследовательская работа позволяет углубленно изучить студентами данную тему.

Целью исследования является накопление и обработка имеющейся информации.

Для достижения цели необходимо решить следующие задачи:

• Изучить историю понятий

• Систематизировать виды интегралов зависящих от параметра

• Составить курс практических заданий.

Объектом исследования являются различные виды интегралов зависящих от параметра в курсе ВУЗов.

В работе использованы следующие методы исследования:

1. Анализ научной литературы

2. Синтез полученных знаний

3. Обобщение всех знаний

Работа насчитывает 24 страницы, состоит из введения, трех глав, заключения, библиографического списка используемой литературы и содержащего 7 наименований, вспомогательные указатели, а также содержит 3 иллюстраций.

Работа может быть использована в качестве методического материала в любых ВУЗах и СУЗах, где углубленно изучается теория интегралов, а также для самостоятельного изучения материала.

Теоретическая значимость данной работы заключается в систематизации материала.

1. Собственные и несобственные интегралы, зависящие от параметра Собственные интегралы зависящие от параметра

Определение интегралов зависящих от параметра

Пусть функция определена в прямоугольнике . Пусть при каждом закрепленном из существует . Ясно, что каждому значению из будет отвечать свое, вполне определенное значение этого интеграла. Следовательно представляет собой функцию переменной (параметра) , определенную в промежутке .

Введем обозначение

(1)

Наша задача будет состоять в том, чтобы, зная свойства функции , получить информацию о свойствах функции . Эти свойства, как будет показано ниже, имеют многообразные применения в особенности при вычислении интегралов.

Допустим еще, что при каждом закрепленном из существует . Тогда этот интервал будет представлять собой функцию переменной (параметра) , определенную в промежутке . Обозначим ее через , так что

( )

О допустимости предельного перехода по параметру под знаком интеграла

Теорема. Пусть функция и пусть - любое из . Тогда.

(1)

Отметим, что существует для каждого значения из , так как при любом закрепленном . В частности существует .

Возьмем - любое. Выберем и закрепим любое .

По условию , поэтому равномерно непрерывна в , и, следовательно, взятому отвечает , зависящее только от , такое, что для любых двух точек из , для которых , оказывается .

Положим , , где - любое, но такое, что , , , где - любое из . Тогда для любого , если , .

Имеем:

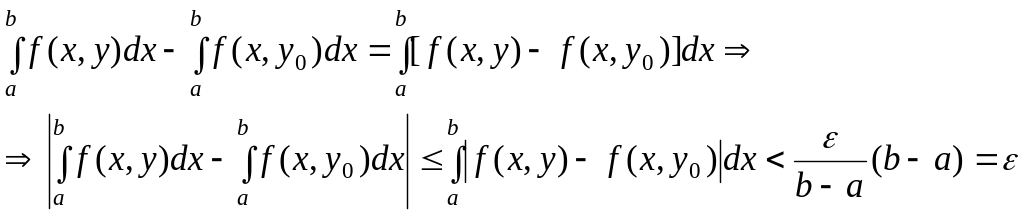
Итак, любому отвечает такое, что как только , , так сейчас же . Последнее означает, что .

Совершенно аналогично доказывается утверждение: Если и если - любое из , то

.