- •Курсовая работа.
- •I.История возникновения дифференциального исчисления
- •1.Определение производной.
- •3.Односторонние производные.
- •3.Дифференцируемость функции.
- •4. Правила вычисления производной.
- •5. Производная и дифференциал сложной функции.
- •6. Основные теоремы дифференциального исчисления.
- •7.Условие постоянства, возрастания и убывания функций.
- •8.Экстремумы функции. Достаточные условия экстремума в терминах первой и высших порядков.
- •9.Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке.
- •III.Применение производной
7.Условие постоянства, возрастания и убывания функций.
Теорема 7.1.
Пусть на [a,b]определена непрерывная функция f(x),имеющая на (a,b) конечную производную.
Тогда:
1)Для того чтобы f(x) была постоянной на [a,b] ,необходимо и достаточно, чтобы f '(x)=0 для всех x из (a,b).
2)для того чтобы f(x)была возрастающей (убывающей ) на [a,b]в широком смысле, необходимо и достаточно, чтобы f’(x)≥0(f’(x)≤0)для всех x из (a,b).
3)для того чтобы f(x) была возрастающей(убывающей) на [a,b] в узком смысле, достаточно выполнения условия f’(x)>0(f’(x)<0) для всех x из (a,b).
Доказательство(см.247 [3])
Замечание.
Обращаем внимание на то, что в данной теореме доказана монотонность функции f(x)в некотором промежутке [a,b] в предположении f (x)≥0(>0) или f (x)≤0(<0)внутри всего этого промежутка. Если же известно ,что f ( )>0(<0) в одной точке ,то отсюда нельзя заключить, что f(x) монотонна хотя бы в малой окрестности точки .в качестве примера рассмотрим функцию:
F(x)=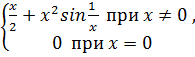 .
.
Ее
производная f’(x)=![]() .значение
f
'(0) из
этой формулы получить нельзя, так как
при x=0
выражение
.значение
f
'(0) из
этой формулы получить нельзя, так как
при x=0
выражение
![]() теряет
смысл. Найдем
теряет
смысл. Найдем
f (0),исходя из определения производной:
![]() .
.
Покажем, что хотя f (x)>0,тем не менее, ни в какой окрестности нуля функция не монотонна. Действительно, если взять точки, то если же взять точки :
![]() ,то,f
,то,f![]()
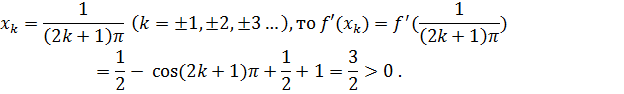
![]() и
и
![]() попадают в любую окрестность нуля т.к
попадают в любую окрестность нуля т.к
![]() и
и ![]() при
при ![]() .следовательно,
производная функции меняет знак в любой
окрестности нуля, что и доказывает наше
утверждение. Этот факт имеет место,
очевидно, из-за того, что производная f
(x)
в
нуле имеет разрыв.
.следовательно,
производная функции меняет знак в любой
окрестности нуля, что и доказывает наше
утверждение. Этот факт имеет место,
очевидно, из-за того, что производная f
(x)
в
нуле имеет разрыв.
Примеры
1.Определить промежутки, на которых функция:
![]() возрастает и убывает в строгом смысле.
возрастает и убывает в строгом смысле.
Находим
производную функции ![]() .
.
Из
неравенств ![]() и получаем ,что данная функция возрастает
на
и получаем ,что данная функция возрастает
на ![]() и
убывает на
и
убывает на ![]() .
.
2.Определить
промежутки возрастания и убывания
функции: ![]() .
.
Находим
производную ![]() .
.
Поскольку
![]() при
всех x,
то и
при
всех x,
то и ![]() на всей числовой оси. Следовательно,
данная функция строго возрастает на
всей оси (
на всей числовой оси. Следовательно,
данная функция строго возрастает на
всей оси (![]() ).
).
8.Экстремумы функции. Достаточные условия экстремума в терминах первой и высших порядков.
Определение 8.1.
Функция
f(
x
) заданная на некотором промежутке,
имеет максимум (минимум) в некоторой
внутренней точке
из
этого промежутка ,если существует такая
окрестность (![]() )точки
,что
для всех x
из этой окрестности(кроме
)
справедливо неравенство
)точки
,что
для всех x
из этой окрестности(кроме
)
справедливо неравенство
f( x )<f( ) , (f( x )>f( )).
Значение f( )в этом случае называют значением максимума (минимума)
Необходимые
условия экстремума. Если точка xо
является точкой экстремума функции f(
x ), то либо f ![]() ( xо ) = 0, либо f
( xо ) не существует.
Такие точки называют критическими,
причем сама функция в критической точке
определена. Экстремумы функции следует
искать среди ее критических точек.
( xо ) = 0, либо f
( xо ) не существует.
Такие точки называют критическими,
причем сама функция в критической точке
определена. Экстремумы функции следует
искать среди ее критических точек.
Первое достаточное условие.
Пусть xо - критическая точка. Если f (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие.
Пусть
функция f(x) имеет
производную
f
( x ) в окрестности точки xо
и вторую производную
![]() в
самой точке xо. Если f
( xо ) = 0,
в
самой точке xо. Если f
( xо ) = 0, ![]() >0
(
>0
(![]() <0), то точка xо
является точкой локального минимума
(максимума) функции f( x ).
Если же
=0, то нужно, либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
<0), то точка xо
является точкой локального минимума
(максимума) функции f( x ).
Если же
=0, то нужно, либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
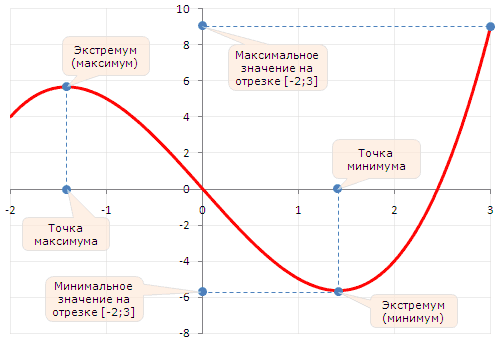
На отрезке [a,b] функция y = f( x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Пример: