3. Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

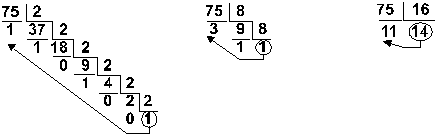
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

4. Перевод правильных десятичных дробей в любую другую позиционную систему счисления

При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.

Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

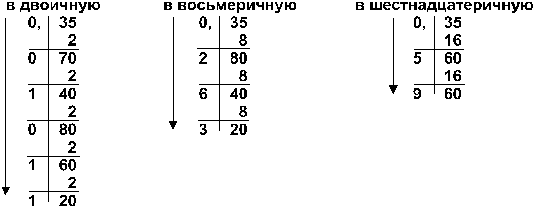
Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆ .

Пример. Перевести десятичное число 315 в шестнадцатеричную систему:

_315 16

16 _ 19 16

155 16 1

144 3

11

315₁₀ = 13В₁₆.

Пример. Перевести десятичную дробь 0,1875 в шестнадцатеричную систему счисления.

0 1 8 7 5 Здесь вертикальная черта отделяет целые части чисел от дробных частей.

^Х 1 6

1 1 2 5 0

1 8 7 5_

3 0 0 0 0

0,1875₁₀ = 0,3₁₆.

5. Перевод чисел из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Пример:

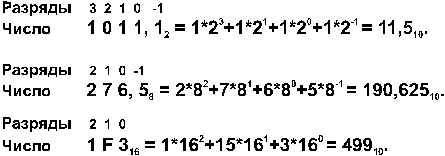
Контрольные вопросы и задания

1. Какие системы счисления называют позиционными, а какие – непозиционными? Приведите примеры.

2. Что называется основанием системы счисления?

3. Какие способы перевода целых десятичных чисел в двоичные и обратно Вы знаете?

4. Как переводить целые числа из двоичного представления в восьмеричное и шестнадцатеричное представление и обратно?

5. Дайте определение системы счисления. Назовите и охарактеризуйте свойства системы счисления.

6. Какие символы используются для записи чисел в двоичной системе счисления, восьмеричной, шестнадцатеричной?

7. Может ли в качестве цифры использоваться символ буквы?

8. Какое количество цифр используется в q-ичной системе счисления?

8

Авторы: Короткова Т.В., Родионова И.В.