2. Реализация задания на компьютере с помощью ппп Ехсеl

С целью повышения эффективности решения задачи необходимо воспользоваться возможностями ППП Ехсеl. Для этого требуется инициировать опцию Мастер функций. В основном будет востребована категория Статистические и некоторые функции из категорий Математические и Ссылки и массивы. Перечень этих функций и краткое описание представлены в Приложении «Стандартные функции».

ВНИМАНИЕ ! Каждый студент должен выполнить индивидуальное задание с использованием компьютера в двух вариантах:

1. Реализовать формулы (1.1) – (1.15) с помощью ППП Ехсеl.

2. Использовать «комплексные» функции, выходом которых являются не только коэффициенты регрессии, но и дополнительная регрессионная статистика (среднеквадратические отклонения, коэффициент детерминации и т.д.).

1. Реализация регрессионных формул (1.1) – (1.15).

В начале необходимо воспользоваться Мастером диаграмм, выбрать тип Точечная и нанести значения выборки на корреляционное поле (рис. 1.1). По расположению точек на графике сделать предварительный анализ о возможной линейной зависимости между переменными.

С помощью функций ППП Ехсеl определить оценки коэффициентов регрессии b₀ , b₁ , реализуя формулы (1.7), (1.8), например , вычисляются с помощью функции СРЗНАЧ, а с помощью функции СУММПРОИЗВ( )/ n. Для вычисления можно воспользоваться соотношением СУММКВ(число1;число2; ...) /n. Однако составляющие коэффициента b₁ можно вычислить проще, через Статистические функции КОВАР(массив1; массив2) Cov (X,Y) и ДИСПР S_x² или СТАНДОТКЛОНП S_x².

По соответствующим формулам вычисляются дисперсии , и на основании Т-статистик делается вывод о значимости коэффициентов регрессии и определяются их доверительные интервалы. Значения t_кр можно получить, используя статистическую функцию СТЬЮДРАСПОБР.

Рис. 1.1.

Примерный вид реализации задачи на компьютере представлен на рис.1.2.

Для графической иллюстрации приближения корреляционной функции и выборочных данных y_i воспользуемся Мастером диаграмм (Точечная) (см. рис.1.3.).

Параметры линейной регрессии можно рассчитать и сразу. Для этого в Ехсеl существуют функции Наклон и Отрезок. Функция Наклон служит для определения углового коэффициента связи (b₁), а функция Отрезок – для определения свободного члена уравнения (b₀). В качестве аргументов этих функций вводятся массивы Х и Y.

Кроме перечисленных возможностей существует еще и следующая возможность. Построим график по имеющимся данным. Чтобы ось Х отражала фактические данные, выберем тип диаграммы Точечная. На построенной диаграмме выделим график функции, щелкнув по ней левой кнопкой мыши. Затем нажмем правую кнопку мыши, выведем контекстное зависимое меню, в котором выберем опцию Добавить линию тренда. В панели линии тренда во вкладке Тип надо выбрать тип функции (по умолчанию выбирается Линейная). Во вкладке Параметры введем название тренда (теоретической кривой) и установим флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». В результате появится график вида (рис.1.4.).

		Парная регрессия (пример)
		y = b0 + b1*x
Введите исходную информацию
Территория	Прожиточный	Среднемесячн	Оценка У	Ошибки Е
региона	минимум (х)	зарплата (у)
1	78	133	148,7700683	-15,77006831
2	82	148	152,4517905	-4,45179052
3	87	134	157,0539433	-23,05394328
4	79	154	149,6904989	4,309501138
5	89	162	158,8948044	3,105195612
6	106	195	174,5421238	20,45787622
7	67	139	138,6453322	0,354667771
8	88	158	157,9743738	0,025626164
9	73	152	144,1679155	7,832084455
10	87	162	157,0539433	4,946056717
11	76	159	146,9292072	12,0707928
12	115	173	182,8259988	-9,825998758
Вычисление по формулам				Al
				0,05
Вспомогательные параметры					Кэфф. регрессии
Хср	Уср	ХУср	ХквСр		В0	В1
85,58333333	155,75	13484	7492,25		76,9764852	0,92043055
КвХср	ЕквСр	УквСр	КвУср		Кху	Rкв
7324,506944	131,2435245	24531,41667	24258,0625		0,72102521	0,51987736
Тв1	Тв0	Ткр	Sb0Кв	Sb1Кв	SКв
3,290594434	3,179327594	2,433444024	586,1997046	0,078240809	157,492229

Рис.1.2.

Рис.1.3.

Рис.1.4.

2. Использование «Комплексных» функций.

Одной из таких функций является встроенная статистическая функция ЛИНЕЙН (описание функции и ее аргументов приведено в приложении «Стандартные функции»).

Дополнительная регрессионная статистика (в случае ее инициализации) будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b1	Значение коэффициента b0
Среднеквадратическое отклонение b1	Среднеквадратическое отклонение b0
Коэффициент детерминации R2	Среднеквадратическое отклонение у
F - статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для данных из вышерассмотренного примера результат вычисления функции ЛИНЕЙН представлен на рис.1.5.

Территория	Прожиточный	Среднемесячн
региона	минимум (х)	зарплата (у)		0,920431	76,97649
1	78	133		0,279716	24,21156
2	82	148		0,519877	12,54959
3	87	134		10,82801	10
4	79	154		1705,328	1574,922
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Рис.1.5.

Примечание. Функция ЛИНЕЙН должна быть введена, как формула массива в интервал с необходимым количеством строк и столбцов. Перед использованием функции ЛИНЕЙН выделяем ячейку (1,1) (1-ая строка, 1-ый столбец) массива, в который будет занесен результат вычисления функции, затем инициализируем Мастер функций, выбираем категорию Статистические и функцию Линейн. Щелкните по кнопке ОК. После заполнения аргументов в ячейке (1,1) появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, выделите массив нужной размерности, включая и ячейку (1,1) (в нашем примере 5 – строк, 2 – столбца), нажмите на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Для лучшей наглядности можно нужные значения из этой таблицы выбирать индивидуально и размещать в нужных форматах документа. Для этого можно воспользоваться функцией ИНДЕКС из категории Ссылки и массивы. Выделите ячейку, в которую хотите поместить отдельный элемент массива и введите формулу, например: Индекс (Линейн (Y; Х; Истина; Истина); 1; 2).

В результате в данную ячейку будет записан элемент (1,2) регрессионной таблицы, т.е. значение b₀. Таким образом можно создать более наглядную таблицу (рис.1.6)

b0	b1	Sb0	Sb1
76,97649	0,920431	24,21156	0,279716
Sy	r2	F -статист	Кол.ст.св	Ss рег		Ss ост
12,54959	0,519877	10,82801	10	1705,328		1574,922

Рис.1.6.

Кроме функции Линейн можно также воспользоваться Статистическим пакетом анализа данных. Чтобы установить пакет Анализа данных в меню Сервис, выберите команду Надстройки и установите флажок Пакет анализа. Диалоговое окно данной опции приведено на рис.1.7.

Чтобы запустить пакет анализа в меню Сервис, выберите команду Анализ данных. В диалоговом окне Анализ данных в списке Инструменты анализа выберите строку Регрессия (рис.1.8).

Примечание. В Ехсеl-2007 установка пакета осуществляется по схеме: «Officе» Параметры Ехсеl Неактивные надстройки приложений Пакет анализа в окне Надстройки (рис.1.7) установить флажок Пакет анализа ОК. Запускается пакет анализа в меню Данные.

Заполните диалоговое окно ввода данных и параметров вывода (рис.1.9):

Входной интервал Y – диапазон, содержащий данные объясняемой переменной;

Входной интервал Х – диапазон, содержащий данные объясняющей переменной;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно задать произвольное имя нового листа.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты регрессионного анализа представлены на рис.1.10.

Рис.1.7.

Рис.1.8.

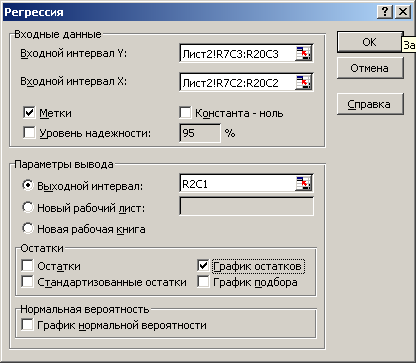
Рис.1.9.

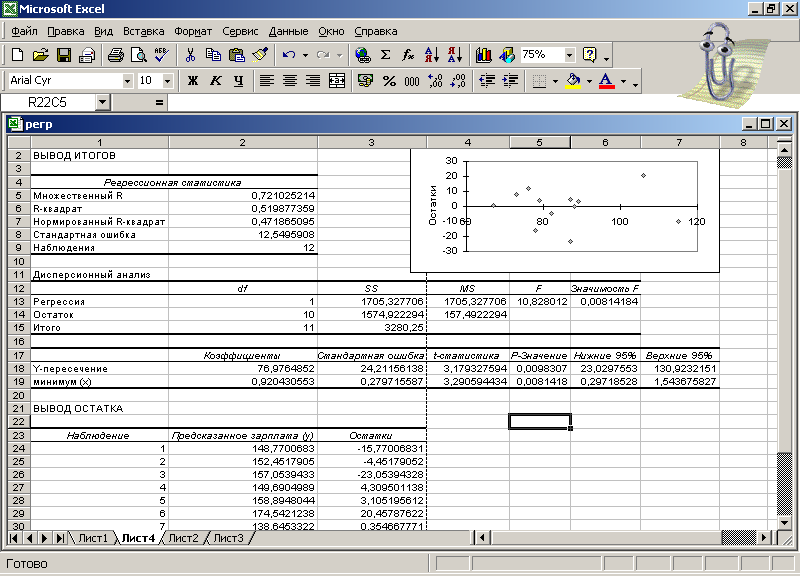
Рис.1.10.

Поясним некоторые обозначения результатов регрессионного анализа:

Множественный R - коэффициент корреляции r_xy;

R-квадрат – коэффициент детерминации;

Стандартная ошибка – СКО объясняемой переменной y;

df - количество степеней свободы;

SS (Регрессия) - объясненная сумма квадратов k_i².

SS (Остаток) - остаточная сумма квадратов e_i² ;

Коэффициенты (Y-пересечение) – b₀;

Коэффициенты (минимум( Х)) – b₁;

Стандартная ошибка(Y-пересечение) – ;

Стандартная ошибка(минимум( Х)) – ;

Нижние (Верхние) – соответствующие границы доверительных интервалов для оценок b₀ и b₁.

Как видно функции Линейн и особенно опция Регрессия выводят большинство показателей, которые до этого были рассчитаны с помощью одиночных функций.