4.2.2. Проверка наличия мультиколлинеарности

Решение данной задачи рассмотрим на Примере 4.1.

Результаты вычислений с помощью ППП Ехсеl представлены на рис.4.5. Парные коэффициенты корреляции (Х₁, Х₂) и (Y, Х₁, Х₂) были получены с помощью функции Корреляция. Доступ к этой функции осуществляется следующим образом:

1) в главном меню выберите Сервис/Анализ данных/Корреляция (рис.4.6). Щелкните по кнопке ОК;

				Корреляция 1
Y	Х1	Х2			Х1	Х2
28,4	635,7	92,9		Х1	1	0,9971653
32	688,1	94,5		Х2	0,9971653	1
37,7	753	97,2
40,6	796,3	100		det R	Хи кв.	Хи кв.кр.
47,7	868,5	104,2		0,0056613	13,874514	5,0238865
52,9	935,5	109,8
58,5	982,4	116,3		Корреляция 2
64	1063,4	121,3			Y	Х1	Х2
75,9	1171,1	125,3		Y	1
94,4	1306,6	133,1		Х1	0,9931772	1
131,9	1412,9	147,7		Х2	0,9926992	0,9971653	1
126,9	1528,8	161,2
155,4	1702,2	170,5		МОБР
185,8	1899,5	181,5		79,150987	-46,02522	-32,67836
217,5	2127,6	195,4		-46,02522	203,40132	-157,1355
260,9	2368,5	217,4		-32,67837	-157,1355	190,12991
Частные коэффициены корреляции
r(Y,X1/X2)	r(Y,X2/X1)	r(X1,X2/Y)
0,362736	0,266383	0,799047

Рис. 4.5

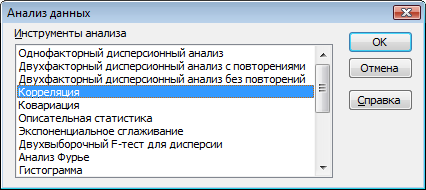
Рис. 4.6

2) заполните диалоговое окно ввода данных и параметров вывода (рис.4.7):

Входной интервал – диапазон, содержащий анализируемые данные;

Группирование – переключатель, указывающий расположение данных по столбцам или по строкам;

Метки – флажок в этой позиции означает, что первая строка исходного диапазона содержит название столбцов;

Параметры вывода – активизируйте выходной интервал и укажите адрес левой верхней ячейки выходного диапазона.

Значения частных коэффициентов корреляции были рассчитаны по формуле (4.24), для этого была обращена матрица R (корреляция 1) при помощи функции МОБР.

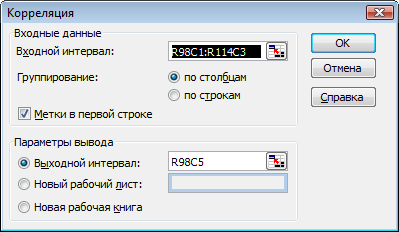
Рис. 4.7

Выводы по задаче:

1) Из рисунка следует, что значения выборочных коэффициентов корреляции указывают на достаточно сильную корреляцию между факторами Х₁, Х₂ ( = 0,997) и частный коэффициент корреляции также высок ( = 0,799), следовательно в модели присутствует мультиколлинеарность. Кроме того det R = 0,0057, т.е. близок к нулю, и проверка с помощью - распределения показала, что (13,87) > (5,024), что также свидетельствует о наличии мультиколлинеарности. Здесь значение было рассчитано по формуле (4.22).

2) Из частных коэффициентов корреляции = 0,363 и = 0,266 следует, что влияние Х₁ на Y больше, чем Х₂ на Y. Частные коэффициенты детерминации = ( )²= 0,132 и = ( )²= 0,071 показывают, что 13,2% рассеивания переменной Y обусловлено изменением только Х₁, а 7,1% - Х₂.