1. Сопоставление на основании произвольного количества значений

Две группы измерений в одной лаборатории

Стандартное отклонение разности двух групп измерений в одной лаборатории в условиях повторяемости

, (2.1)

где – дисперсия повторяемости;

n₁ = n₂ = 20 – количество измерений в каждой группе.

Средние арифметические значения в группах измерений в первой лаборатории

;

.

Разность двух групп измерений в одной лаборатории

.

Внутрилабораторные дисперсии в первой лаборатории

;

.

Дисперсия повторяемости в первой лаборатории

; .

Стандартное отклонение разности двух групп измерений

.

Критическая разность для на уровне вероятности 95%

. (2.2)

,

то есть две группы измерений в одной лаборатории не согласованы.

Две группы измерений в двух лабораториях

В первой лаборатории количество измерений n₁ = 40, во второй n₂ = 20.

Средние арифметические значения в группах измерений

;

.

Разность двух групп измерений в разных лабораториях

.

Стандартное отклонение разности в условиях повторяемости

, (2.3)

, (2.4)

, (2.5)

, (2.6)

; (2.7)

. (2.8)

;

;

;

.

Среднее значение результатов измерений в лаборатории 1 = 7,721, в лаборатории 2 = 7,6765, в двух лабораториях

.

.

Стандартное отклонение разности двух групп измерений в разных лабораториях

.

Критическая разность для на уровне вероятности 95%

, (2.9)

где – дисперсия воспроизводимости, .

= 0,0033 + 0,000866 = 0,004167;

> 0,0445.

Полученный результат дает основание говорить о согласованности результатов измерений двух лабораторий.

Группа измерений в одной лаборатории и опорное значение

Стандартное отклонение разности для каждой лаборатории, где μ₀ = 7,7 – принятое опорное значение

. (2.10)

Для первой лаборатории n₁ = 40; .

Для второй лаборатории n₂ = 20; .

Разность группы измерений и опорного значения в первой лаборатории ; разность группы измерений и опорного значения во второй лаборатории .

Критическая разность для одной лаборатории

, (2.11)

для первой лаборатории

;

для второй лаборатории

.

Полученные результаты дают основание говорить о согласованности результатов измерений каждой из двух лабораторий с опорным значением.

Группы измерений в двух лабораториях и опорное значение

Разность двух групп измерений и опорного значения

.

Стандартное отклонение разности для нескольких лабораторий

. (2.12)

Стандартное отклонение разности для двух лабораторий

, (2.13)

.

Критическая разность для двух лабораторий

.

Полученный результат дает основание говорить о согласованности результатов измерений двух лабораторий с опорным значением.

Таким образом, при проведении сопоставления:

а) двух групп измерений в одной лаборатории

CD_0,95 = 0,035631, = 0,037;

б) двух групп измерений в разных лабораториях

CD_0,95 = 0,088106, = 0,0445;

в) группы измерения в одной лаборатории с опорным значением

CD_0,95 = 0,060988, ; CD_0,95 = 0,063585, ;

г) двух групп измерений в разных лабораториях с опорным значением

CD_0,95 = 0,044053, = 0,006.

Можно сделать вывод, что почти во всех экспериментах абсолютное расхождение не превышает соответствующий предел и лишь при проведении двух групп измерений в одной лаборатории (а) абсолютное расхождение превышает критическую разность, что должно рассматриваться как подозрительное и подлежащее дополнительному изучению.

2. Проверка приемлемости результатов измерений и установления окончательного результата

Для двух измерений в каждой лаборатории дисперсии повторяемости

; ; ;

Стандартные отклонения повторяемости:

σ_1r = 0,035355; σ_2r = 0,000000; σ_3r = 0,014142.

Абсолютные расхождения

x_1max – x_1min = 0,0500; x_2max – x_2min = 0,0000; x_3max – x_3min = 0,0200.

В условиях повторяемости критическую разность и стандартное отклонение повторяемости связывает табулированная функция f(n) (табл. 2.2)

CD_0,95 = r = f(n) σ_r. (2.13)

Для n = 2 критическая разность CD_0,95 = 2,8σ_r, в этом случае пределы повторяемости для каждой лаборатории:

r₁ = 2,80,35355 = 0,098995; r₂ = 0,000000; r₃ = 0,039598.

Проверка приемлемости результатов выполняется в виде последовательности этапов сравнения абсолютных расхождений результатов измерений с критическими разностями.

Таблица 2.2

Коэффициенты критического диапазона f(n)

n	f(n)	n	f(n)	n	f(n)
2	2,8	18	4,9	34	5,4
3	3,3	19	5,0	35	5,4
4	3,6	20	5,0	36	5,4
5	3,9	21	5,0	37	5,4
6	4,0	22	5,1	38	5,5
7	4,2	23	5,1	39	5,5
8	4,3	24	5,1	40	5,5
9	4,4	25	5,2	45	5,6
10	4,5	26	5,2	50	5,6
11	4,6	27	5,2	60	5,8
12	4,6	28	5,3	70	5,9
13	4,7	29	5,3	80	5,9
14	4,7	30	5,3	90	6,0
15	4,8	31	5,3	100	6,1
16	4,8	32	5,3
17	4,9	33	5,4

На рис. 2.1 изображен алгоритм определения результата измерения в случае, если измерения не являются дорогостоящими.

Рис. 2.1. Алгоритм определения результата измерений, не являющихся дорогостоящими

На первом этапе сравнивают абсолютные расхождения с критическими разностями и определяют итоговый результат по двум измерениям.

x_1max – x_1min  r₁, 0,05  0,098995; x_2max – x_2min  r₂, 0  0;

x_3max – x_3min  r₃, 0,02  0,039598.

= (7,75+7,8)/2 = 7,775; = (7,7+7,7)/2 = 7,7; = (7,72+7,74)/2 = 7,73.

В случае невыполнения условий сравнения на втором этапе проводят еще два измерения в каждой лаборатории, при этом стандартные отклонения повторяемости: σ_1r = 0,047871; σ_2r = 0,047871; σ_3r = 0,014142.

Абсолютные расхождения:

x_1max – x_1min = 0,10; x_2max – x_2min = 0,10; x_3max – x_3min = 0,03.

Для n = 4 критическая разность CD_0,95 = 3,6σ_r, пределы повторяемости:

r₁ = 0,172337; r₂ = 0,172337; r₃ = 0,050912.

Сравнение абсолютных расхождений с критическими разностями

x_1max – x_1min  r₁, 0,1  0,172337; x_2max – x_2min  r₂, 0,1  0,172337;

x_3max – x_3min  r₃, 0,03  0,050912.

Итоговый результат по четырем измерениям

; ;

.

В случае невыполнения условий сравнения на третьем этапе из четырех результатов измерения выбирают второй и третий наименьшие результаты и рассчитывают их среднее арифметическое. Полученные результаты будут считаться окончательными.

; ; .

Так как на первом этапе для всех лабораторий x_max – x_min ≤ CD_0,95, то в этом случае окончательнным результатом будет x₁ = 7,775; x₂ = 7,7; x₃ = 7,73.

На рис. 2.2 изображен алгоритм определения результата измерения в случае, если измерения являются дорогостоящими.

В этом случае первый этап аналогичен первому этапу предыдущего алгоритма. При невыполнении условий сравнения на втором этапе проводят еще одно измерение в каждой лаборатории, при этом стандартные отклонения повторяемости: σ_1r = 0,05; σ_2r = 0,028868; σ_3r = 0,015275.

Абсолютные расхождения:

x_1max – x_1min = 0,10; x_2max – x_2min = 0,05; x_3max – x_3min = 0,03.

Для n = 3 критическая разность CD_0,95 = 3,3σ_r, при этом пределы повторяемости: r₁ = 0,165; r₂ = 0,095263; r₃ = 0,050408.

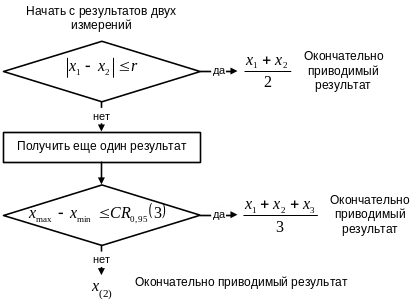
Рис. 2.2. Алгоритм определения результата измерений, являющихся дорогостоящими

Сравнение абсолютных расхождений с критическими разностями

x_1max – x_1min  r₁, 0,1  0,165; x_2max – x_2min  r₂, 0,05  0,095263;

x_3max – x_3min  r₃, 0,03  0,050408.

Итоговый результат по трем измерениям

; ;

.

В случае невыполнения условий сравнения на третьем этапе в каждой лаборатории из трех результатов измерения выбирают второй наименьший результат. Полученные результаты будут считаться окончательными:

; ; .

Так как на первом этапе для всех лабораторий x_max – x_min ≤ CD_0,95, то для первоначальных двух измерений окончательнным результатом будет x₁ = 7,775; x₂ = 7,7; x₃ = 7,73.

На рис. 2.3 изображен алгоритм определения результата измерения для случая с более, чем двумя первоначальными измерениями.

Выбираем n = 10 значений в качестве групп первоначальных измерений в каждой из трех лабораторий (табл. 2.1).

Стандартные отклонения повторяемости:

σ_1r = 0,062902; σ_2r = 0,053748; σ_3r = 0,044522.

Абсолютные расхождения:

x_1max – x_1min = 0,2000; x_2max – x_2min = 0,1500; x_3max – x_3min = 0,1500.

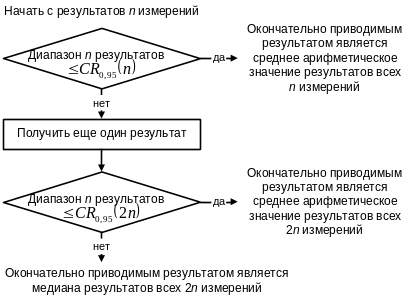
Рис. 2.3. Алгоритм определения результата измерения для случая

с более, чем двумя первоначальными измерениями

Пределы повторяемости r = 4,5σ_r:

r₁ = 0,283059; r₂ = 0,241868; r₃ = 0,200350.

Сравнение абсолютных расхождений с критическими разностями

x_1max – x_1min  r₁, 0,2  0,283059; x_2max – x_2min  r₂, 0,15  0,241868;

x_3max – x_3min  r₃, 0,15  0,200350.

Итоговый результат по десяти измерениям определяется в виде средних арифметических значений

= 7,743; = 7,68; = 7,724.

В данном случае абсолютные расхождения не превышают соответствующих пределов во всех лабораториях, поэтому окончательными результатами будут x₁ = 7,743; x₂ = 7,68; x₃ = 7,724.

В случае, если такое превышение существует, необходимо выбрать количество измерений в два раза больше первоначального.

Выбираем 2n = 20 значений в качестве вторичных измерений по трем лабораториям (табл. 2.1).

Стандартные отклонения повторяемости:

σ_1r = 0,065412; σ_2r = 0,053634; σ_3r = 0,042302.

Абсолютные расхождения:

x_1max – x_1min = 0,2500; x_2max – x_2min = 0,1800; x_3max – x_3min = 0,1500.

Пределы повторяемости r = 5,0σ_r:

r₁ = 0,327058; r₂ = 0,268169; r₃ = 0,211511.

Сравнение абсолютных расхождений с критическими разностями

x_1max – x_1min  r₁, 0,25  0,327058; x_2max – x_2min  r₂, 0,18  0,268169;

x_3max – x_3min  r₃, 0,15  0,211511.

Итоговый результат по двадцати измерениям определяется в виде средних арифметических значений

= 7,7395; = 7,6765; = 7,7200.

В данном случае абсолютные расхождения не превышают соответствующих пределов во всех лабораториях. Поэтому окончательными результатами будут x₁ = 7,7395; x₂ = 7,6765; x₃ = 7,72.

В случае, если соответствующие пределы будут превышены, то в качестве окончательного результата выбираются медианы:

= 7,735; = 7,655; = 7,72.

Так как на первом этапе для всех лабораторий x_max – x_min ≤ CD_0,95, то для первоначальных десяти измерений окончательнным результатом будет x₁ = 7,743; x₂ = 7,68; x₃ = 7,724.