3.3. Вероятность поражения целей

Вероятность попадания, показывая степень объективной возможно­сти попадания в цель, уже является некоторым критерием, определяю­щим действительность данной стрельбы. Однако сама по себе вероят­ность попадания не дает ответа на целый ряд практических вопросов, знание которых необходимо для эффективного использования оружия. Так, вероятность попадания не отвечает на вопрос о том, сколько в среднем можно ожидать попаданий в цель, если при данной вероятности попадания по ней будет израсходовано определенное количество боепри­пасов, или какова вероятность попасть в цель хотя бы одним снарядом, или какой процент пораженных фигур можно рассчитывать при стрельбе данным количеством патронов по групповой цели.

Решение подобных вопросов связано с понятиями о вероятности по­ражения цели и математическом ожидании числа попаданий в цель.

Математическое ожидание числа попаданий

В практике стрельбы часто надо знать, на какое количество попада­ний в среднем можно рассчитывать, если в данных условиях по цели будет произведено определенное количество выстрелов.

Из главы «Сведения из теории вероятностей» известно, что среднее ожидаемое значение какой-либо случайной величины называется мате­матическим ожиданием данной величины. Математическое ожидание оп­ределяется как сумма парных произведений частных значений данной величины на соответствующую ей вероятность:

МОЖ(Х) = Х₁·Р₁ + Х₂·Р₂+ …+Х_n ·P_n.

Таким образом, математическое ожидание числа попаданий при од­ном выстреле (a₁) найдется из выражения:

МОЖ (числа попаданий) =а₁ = 1 · Р_ф +0 · q,

где а₁ – математическое ожидание числа попаданий при одном выстреле;

Р_ф – вероятность попадания в фигуру;

q – вероятность промаха, равная (1-Р_ф).

Так как второй член произведения равен нулю, можно записать: а₁=Р_ф, т. е. При одном выстреле математическое ожидание числа попа­даний численно равно вероятности попадания.

Необходимо помнить, что это равенство только численное, т. к. ма­тематическое ожидание числа попаданий в отличие от вероятности попа­дания есть именованное число. Оно может быть целым, дробным, большим чем единица и вообще любым именованным числом, в то время как вероятность попадания отвлеченное число, которое не бывает меньше нуля и больше единицы.

Математическое ожидание числа попаданий при нескольких выстре­лах определяется на основе одной из теорем теории вероятностей, кото­рая читается следующим образом.

Математическое ожидание суммы событий равно сумме математических ожиданий этих событий:

a_n=a₁ + а₂ + а₃ + . . . +а_n.

Пример. Определить математическое ожидание числа попаданий в танк, двигающийся на огневую позицию противотанкового орудия, если по нему будет произведено 3 выстрела со следующими вероятностями по­падания: 0,3; 0,6; 0,9.

Решение. 1. Математическое ожидание числа попаданий при каж­дом выстреле численно равно вероятности попадания.

А) При первом выстреле: а₁ = р₁=0,3 попадания.

Б) При втором выстреле: а₂=р₂ =0,6 попадания.

В)При третьем выстреле: а₃=р₃=0,9 попадания.

3. На основе вышеприведенной теоремы определим математическое ожидание числа попаданий при трех выстрелах:

а_з=а₁ + а₂ + а₃=0,3+0,6+0,9=1,8 попаданий.

Если вероятность попадания от выстрела к выстрелу не изменяется, то математические ожидания числа попаданий при каждом выстреле будут равными между собой. В этом случае можно записать: а_n =n·a₁ или, учитывая, что a₁ = Р, а_n = n· Р,

где n – число предпо­лагаемых выстрелов.

Математическое ожидание числа попаданий есть среднее возмож­ное число попаданий, которое может быть получено при большом числе выстрелов в возможно одинаковых условиях.

Пример. Определить, сколько в среднем можно ожидать попаданий при стрельбе короткими очередями по поясной мишени из автомата Ка­лашникова (АК74) на дальность 200 м, если СТП совпадает с серединой нижнего обреза цели и по цели будет израсходовано 9 патронов.

Решение. 1. Определим вероятность попадания в фигуру

Вц=Вб =0,11 м.

; ; .

; ; Pб=Ф(2,27)=0,874.

Рф=Рв·Рб; Рф=0,5·0,874=0,437.

К_ф в данном случае применять не следует, так как фигурные очер­тания цели выходят за пределы эллипса рассеивания.

4. Определим среднее ожидаемое число попаданий.

A_n = n·р; а_n=9·0,437=3,933; а_n≈ 4 попадания.

Найденный ответ «≈4 попадания» необходимо понимать следующим образом. При каждой отдельной стрельбе может быть различное число попаданий: от нуля (все промахи) до 9 попаданий. Однако, при большом числе аналогичных стрельб в среднем на каждые 9 выстрелов будет при­ходиться 4 попадания.

Формула а_n =n ·р применима для определения математического ожидания числа попаданий в цель при стрельбе как одиночными выст­релами, так и очередями (залпами) при условии, что вероятность попа­дания р от выстрела к выстрелу не изменяется.

При стрельбе очередями, когда вероятность попадания первых (Р₁) и последующих (Р_посл.) снарядов (пуль) неодинакова, математическое ожидание числа попаданий можно определить по формуле:

А_n =n₁·P₁+ n_посл.·P_посл.,

где n₁ – число первых снарядов (пуль);

P₁ – вероятность попадания каждого из первых снарядов (пуль);

n_посл. – число последующих снарядов в очереди;

Р_посл. – вероятность попадания последующих снарядов очереди.

Пример. Определить математическое ожидание числа попаданий при стрельбе тремя очередями, если общее число всех выстрелов равно 12, а вероятность попадания для каждого первого Р₁ =0,2, а для каждо­го последующего Р_посл. =0,1.

Решение. А_n=n₁ · P₁ + n_посл.· Р_посл. = 3·0,2+9·0,1 = 1,5 попадания.

Вероятность поражения цели (надежность стрельбы)

Математическое ожидание числа попаданий, являясь определенным показателем эффективности стрельбы, не дает, однако, ответа на вопрос о том, как часто может быть получен данный результат, то есть не отве­чает на вопрос о том, какова вероятность того, что при первой же стрельбе будет получено 5, 4, 3, 2 или хотя бы одно попадание в цель.

При стрельбе по живой цели достаточно получить хотя бы одно попадание, чтобы вывести ее из строя; поэтому вероятность попасть хотя бы один раз при заданном числе выстрелов называется вероятностью по­ражения живой цели или надежностью стрельбы.

Из определения вероятности поражения цели (надежности стрель­бы) видно, что вероятность поражения будет определяться по формуле вероятности появления события хотя бы один раз, выведенной в главе «Сведения из теории вероятностей»:

Р₁=1-(1-р)ⁿ,

где Р₁ – вероятность поражения цели (надежность стрельбы) или ве­роятность появления события хотя бы один раз;

р – вероятность попадания при одном выстреле;

n – число выстрелов.

Пример. Пулеметчик ПКМ ведет огонь по грудной мишени на рас­стоянии 400 метров очередями в 5 патронов. Какова вероятность того, что цель будет поражена первой очередью? Стрельба ведется легкой пу­лей, СТП совпадает с центром цели.

Решение. 1. Определим вероятность попадания в грудную мишень (по приведенным размерам цели).

Рв=0,517.

; Рб=0,401.

Рф=0,517· 0,401 = 0,207; Рф,=0,207.

5. Определим вероятность поражения цели при стрельбе 5-ю патро­нами

Р₁=1-(1-р)^п; р₁ = 1- (1-0,207)⁵=1- 0,793⁵=0,687.

Таким образом, при стрельбе в данных условиях вероятность пора­зить цель первой (так же как и любой последующей) очередью в 5 патро­нов равна 0,69.

Найденная вероятность, отвечая на вопрос о том, как часто может быть выполнена поставленная задача, характеризует степень надежно­сти данной стрельбы. Поэтому вероятность попасть хотя бы один раз в данных условиях, кроме вероятности поражения, называют еще надеж­ностью стрельбы.

Из анализа формулы видно, что вероятность поражения цели (на­дежность стрельбы) зависит от вероятности попадания и от числа выст­релов. При одном выстреле вероятность поражения равна вероятности попадания Р₁₌р. Чем больше вероятность попадания и число выстре­лов, тем надежнее стрельба.

Для повышения надежности стрельбы по одиночным целям в боевых условиях используют оба эти направления: или стремятся повысить ве­роятности попадания (например, огонь снайперов), или увеличивают количество патронов (применение сосредоточенного огня нескольких огневых средств).

Рассмотренная нами формула Р₁ =(1-р)ⁿ применима для оп­ределения вероятности поражения не только одиночными выстрелами, но и очередями (залпами) при условии, если вероятность попадания р от выстрела к выстрелу не изменяется.

В предыдущей главе было отмечено, что при стрельбе очередями рассеивание последующих снарядов в очереди может быть больше рассеивания пер­вых и, кроме того, между СТП первых и последующих снарядов может быть некоторый разрыв.

В таких случаях вероятность попадания каждого последующего снаряда (пули) будет отличаться от вероятности попадания первого снаряда (пули) в каждой очереди выстрелов.

Порядок определения вероятности поражения цели в этом случае мо­жет быть следующим.

Пример. Стрельба ведется из автомата Калашникова по грудной фи­гуре на дальность 300 м. Определить вероятность поражения цели при стрельбе двумя очередями по три выстрела в каждой, если средняя точ­ка попадания первых и последующих пуль совпадает с центром цели.

Решение. По таблицам стрельбы (ТС № 63 ГРАУ) находим:

• при стрельбе одиночными выстрелами Вв=0,10 м, Вб=0,10 м;

• при стрельбе очередями Вв=0,17 м; Вб=0,17 м.

Высота цели 2у¹=0,42 м, ширина 2z¹ =0,42 м (приведенные разме­ры цели).

6. Определим вероятность поражения цели первыми (двумя) выст­релами очередей.

а) Находим вероятность попадания в цель

; ; рв=0,843.

; ; рб=0,843.

Рф = Р_в · Рб ; Рф =0,843 ·0,843=0,71 или 71%.

б) Находим вероятность поражения цели первыми пулями очередей Р_1посл.-(1-р_посл.)ⁿ=1-(1-0,71)² = 0,916.

7. Определим вероятность поражения цели последующими (четырь­мя) выстрелами.

а) Находим вероятность попадания в цель

; Рв=0,593.

; Рб=0,593.

Р_посл.=0,593·0,593=0,353.

б) Находим вероятность поражения

Р_{I посл.} = 1-(1-р_посл.)ⁿ =1-(1-0,353)⁴ = 0,825.

8. Определим вероятность поражения цели с учетом и первых, и последующих выстрелов.

Вероятность непоражения цели только первыми выстрелами равна 1-Р_I,1 =1-0,916=0,084 и только последующими выстрелами 1- Р_{I посл.} =1 – 0,825= =0,175.

Вероятность того, что цель не будет поражена при всех шести выст­релах, равна (1-Р_I,1)·( 1- Р_{I посл.}) = 0,084·0,175 = 0,015.

Вероятность поражения цели при стрельбе очередями (Р_{I оч.})с уче­том первых и последующих выстрелов равна Р_{I оч}. =1-0,015=0,985.

Пример. Все условия задачи те же, что и в предыдущем примере, но средняя точка попадания последующих выстрелов левее центра цели на 20 см и ниже его на 20 см (рис. 62).

Решение. 1. Вероятность поражения цели первыми (двумя) выстре­лами Р_I,1 =0,916 (как в предыдущем примере).

9. Определим вероятность поражения цели последующими (четырь­мя) выстрелами.

а) Находим вероятность попадания.

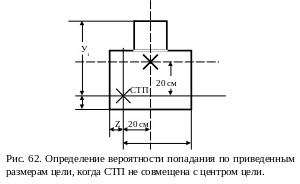
Hа рис. 62 видно, что у₁=0,41 м; у₂=0,01 м; z₁=0,41 м; z₂ = 0,01 м.

; ; .

; ; .

Рв=Рв₁+Рв₂; Рв=0,448+0,016=0,464.

; ; .

; ; .

Рб= Рб₁+Рб₂; Рб=0,448+0,016=0,464.

Р_посл.=Рв+Рб; Р_посл.=0,464·0,464≈0,215.

б) Находим вероятность пора­жения цели последующими выстре­лами

P_i, _поcл. =1 – (1- Р_посл.)ⁿ ; P_{i поcл}.=1-(1-0,215)⁴=0,62.

в) Находим вероятность поражения цели при стрельбе обеими очередями Р₁, _оч. = 1 – (1 – 0,916)· (1 – 0,62) =1 –0,084·0,38=0,968.

Если стрельба ведется несколь­кими одинаковыми очередями, по­рядок определения вероятности по­ражения целей может быть еще и такой:

1. Определить вероятность по­ражения цели при стрельбе одной очередью (вышеописанным спосо­бом).

2. Определить вероятность поражения цели при стрельбе заданным числом очередей по формуле:

р_i,оч. = 1 — (1 — Р_1,оч.)ⁿ,

где Р_{1, оч}. – вероятность поражения цели одной очередью;

n – число таких очередей.

Решим этим способом ту же задачу, что и в первом примере.

1. Вероятность поражения цели последующими двумя выстрелами очереди равна: Р_{1, посл}. =1-(1- 0,353)²=1- 0,647²=1- 0,418=0,582.

2. Вероятность поражения при стрельбе одной очередью равна:

Р_{1, оч}. = 1-(1-0,916)·(1-0,582) =1- 0,084 · 0,418 = 0,965.

Вероятность поражения цели двумя очередями равна

Р_{1, оч}.= 1- (1-0,965) ²=1-0,012=0,988.

Как видим, вероятность поражения цели такая же, как и в первом примере. Поэтому гораздо удобнее производить расчеты вероятности по­ражения цели при стрельбе несколькими очередями по приведенной формуле.

Для определения вероятности поражения одиночных целей при ус­ловии, что вероятность попадания от выстрела к выстрелу не меняется, можно пользоваться приложением № 1.

Данная таблица представляет собой рассчитанную формулу Р₁ = 1-(1-р)^п для различной величины вероятности попадания и числа выстрелов.

После того, как будет найдена вероятность попадания в мишень, например, р=0,28, вероятность поражения находится по таблице следую­щим образом: в вертикальном столбце находим значение вероятности попадания р=0,28, а в горизонтальной строчке против числа, соответст­вующего числу выстрелов n, находим вероятность поражения цели (на­дежность стрельбы), например, при пяти выстрелах – 0,81.

Пользование этой таблицей облегчает решение целого ряда задач. Однако она не оказывает помощи в решении задач при большом числе выстрелов. Для облегчения решения этой задачи пользуются зависимо­стью между математическим ожиданием числа попаданий и вероятно­стью поражения цели.

Зависимость между математическим ожиданием числа попаданий и вероятностью поражения (надежностью стрельбы)

Анализируя формулы для определения математического ожидания числа попаданий (а_n = n · р) и для определения вероятности пора­жения

(Р_i =1-(1-р)ⁿ), можно увидеть, что обе эти величины зависят от ве­роятности попадания и числа выстрелов. Вполне естественно, что эти две величины связаны между собой определенной зависимостью: чем больше математическое ожидание числа попаданий, тем больше вероят­ность поражения цели. (Исключение представляет случай, когда вероят­ность попадания равна нулю или единице).

Это положение позволяет составить специальные таблицы для пере­хода от математического ожидания числа попаданий к вероятности по­ражения.

Однако составление и пользование такими таблицами осложняется тем, что характер зависимости между математическим ожиданием числа попаданий и вероятностью поражения изменяется с изменением вероят­ности попадания. Например, при вероятности попадания, равной едини­це, увеличение количества выстрелов будет систематически увеличивать математическое ожидание числа попаданий. Однако вероятность пора­жения P₁ все время будет оставаться равной единице.

Для перехода от вероятности поражения к математическому ожида­нию числа попаданий можно пользоваться приложением № 1, составленным для вероятности попадания, равной 0,1. (Практически этим приложением можно пользоваться при вероятности попадания, не пре­вышающей 0,3 – 0,4).

Наличие такого приложения значительно облегчает решение задач по определению вероятности поражения цели, т. к. вместо решения формулы

P_i =1- (1-р)ⁿ , где приходится возводить дробное число в «n-ную» степень, можно решить формулу а_n= n·р и по приложению № 1 определить значение вероятности поражения.

Решение вышеприведенного примера с помощью таблицы выгляде­ло бы следующим образом.

После определения вероятности попадания в фигуру Р_ф = 0,28 надо определить математическое ожидание числа попаданий при 5 выстрелах.

А_n =n·р; а_n =5·0,28= 1,4 попадания.

По данному значению а_п = 1,4 попадания по приложению №1 определя­ем, что вероятность поражения равна 0,772. Небольшое расхождение в значении вероятности поражения (Р₁), рассчитанной по формуле и определенной по таблице, получается в результате того, что таблица рассчи­тана для вероятности попадания, равной 0,1, а в нашем примере вероят­ность попадания равна 0,28.

Таким образом, наличие приложения № 2 позволяет быстро переходить от вероятности поражения к математическому ожиданию числа попада­ния и обратно, что особенно удобно при определении процента поражен­ных фигур групповой цели и при определении количества патронов, не­обходимых для выполнения той или иной огневой задачи.

Математическое ожидание числа пораженных фигур групповой цели

Степень наносимого поражения при стрельбе по групповым целям определяется числом (процентом) пораженных фигур, входящих в дан­ную цель. Считают, что огонь на уничтожение групповой цели соответствует поражению 80 % фигур цели, огонь на подавление соответствует по­ражению 50% фигур цели. Решая огневую задачу, необходимо иметь представление о том, каково может быть поражение цели при израсхо­довании данного количества патронов.

Для определения процента пораженных фигур при стрельбе по широ­ким целям из пулеметов применяется рассмотренная выше таблица № 1, показывающая зависимость между математическим ожи­данием числа попаданий в одну фигуру и вероятностью поражения этой фигуры.

Сущность решения задачи сводится к следующему.

Пусть на фронте АВ имеется несколько перебегающих фигур. Тре­буется определить средний процент пораженных фигур групповой цели, если по цели будет израсходовано n патронов.

Для решения этой задачи прежде всего необходимо определить ве­роятность попадания в одну из фигур данной групповой цели:

.

Зная вероятность попадания в одну фигуру и число патронов n, по формуле Р₁ = 1- (1- р)ⁿ определим вероятность поражения одной фи­гуры.

Так как при определении вероятности попадания и поражения этой фигуры мы не задавались определенным положением этой фигуры, то, следовательно, она будет иметь приведенную вероятность поражения на лю­бом участке обстреливаемого фронта. Отсюда понятно, что сколько бы подобных фигур не было на данном фронте, все они будут иметь одина­ковую вероятность поражения P₁. Так как P₁ показывает вероятность поражения фигуры при данной стрельбе, то вполне естественно, что при этой стрельбе процент пораженных фигур будет равен вероятности пора­жения одной фигуры, выраженной также в процентах.

Таким образом, для определения процента пораженных фигур груп­повой цели необходимо:

а) Определить вероятность попадания в одну фигуру.

Б) По найденной вероятности попадания и числу патронов, по формуле Р₁=1-(1-р)ⁿ определить вероятность поражения одной фигуры цели. Вероятность поражения одной фигуры цели численно равна про­центу пораженных фигур.

Пример. На удалении 500 м от пулемета на фронте 20 м замечена группа перебегающих солдат противника. Какой можно ожидать про­цент пораженных фигур, если по цели будет израсходовано 40 патронов? Огонь ведется пулей обр. 1908г. Ось рассеивания проходит через сере­дину высоты фигур.

Решение. 1. Определим вероятность попадания в одну фигуру.

Вв=0,19 м; так как стрельба ведется с рассеиванием по фронту, то для определения входного числа необходимо Вв увеличить в 1,75 раза.

; ;

Рв= Ф(2,27) = 0,874; .

10. Определим вероятность поражения одной фигуры, если по цели израсходовано 40 патронов.

Р₁ = 1(1- р)ⁿ; P₁ = 1- (1- 0,017)⁴⁰=0,51; Р₁=51%.

Таким образом, при стрельбе в данных условиях мы можем в сред­нем ожидать 51% пораженных фигур.

Эту же задачу проще решать используя приложение № 2, которое по математическому ожиданию числа попаданий в 1 фигуру дает значение вероятности поражения данной фигуры; последняя, как мы видели выше, численно равна проценту пораженных фигур групповой цели.

Решение вышеприведенной задачи по приложению № 2 осуществляется следующим образом.

После определения вероятности попадания в одну фигуру групповой цели необходимо найти математическое ожидание числа попаданий в эту фигуру при 40 выстрелах,

а_n = n·р; а_n = 40 ·0,017 = 0,68 попадания.

Затем по таблице найдем, что данному числу а_п =0,68 попаданий со­ответствует вероятность поражения, равная 0,51. Это и есть ожидаемый процент пораженных фигур.

Так решается вопрос о поражении групповых и одиночных целей при заданном числе выстрелов.