2.5 Зависимость между мерами рассеивания. Соотношение между величинами рассеивания по высоте и по дальности

При рассмотрении зависимости между мерами рассеивания следует подчеркнуть, что все применяемые для характеристики рассеивания ме­ры имеют определенную связь друг с другом, так как все они выражают количественную характеристику одного и того же явления.

Установим сначала зависимость между сердцевинной полосой и сре­динным отклонением.

Из теории ошибок известно, что

или

г де В - вероятное отклонение, В₂ - среднее квадратическое отклонение. Указанную зависимость можно записать так:

откуда 3В=2В₂.

Но два средних квадратических отклонения по ширине равны серд­цевинной полосе, следовательно, С = ЗВ. По высоте Св = ЗВв; по дально­сти Сд=ЗВд; по боковому направлению Сб=ЗВб.

Таким образом, сердцевинная полоса равна трем соответствующим срединным отклонениям (по полтора отклонения в каждую сторону).

Рассмотрим зависимость между срединным (вероятным) отклоне­нием и радиусом круга, вмещающего 50% всех пробоин.

Теория стрельбы установила зависимость между срединным откло­нением В и радиусом R₅₀. Радиус круга, содержащего 50% попаданий, R₅₀=1,76B.

Можно показать, допустив некоторые приближения, этот вывод сле­дующим образом. При равенстве Св и Сб сердцевина рассеивания представляет собой квадрат со стороной Св=Сб =С. Площадь сердцевины С² приравняем к площади круга, вмещающего в себя 50% всех попаданий (точек встречи):

С²=πR²;

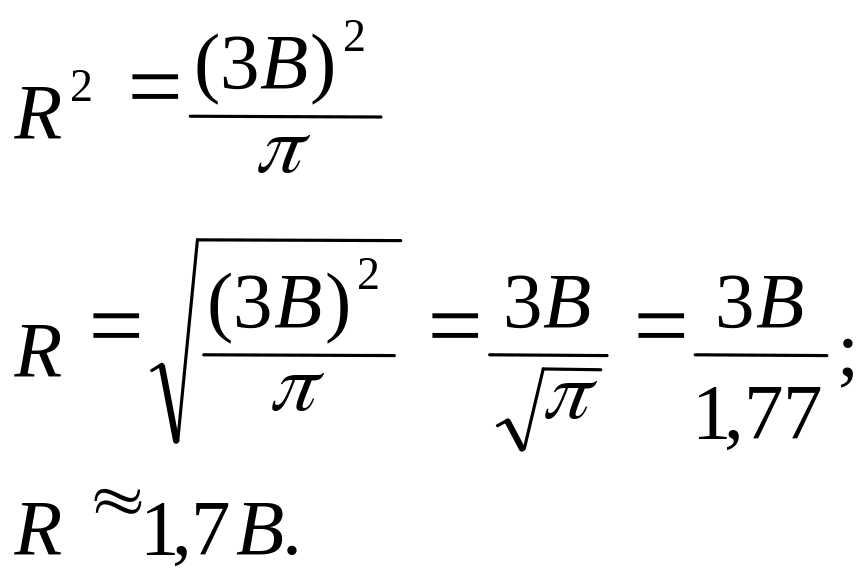( 3В)²=πR²;

Пользуясь этой зависимостью и зная величину срединного отклоне­ния, легко найти величину радиуса круга, вмещающего лучшую полови­ну попаданий.

Пример: При стрельбе из автомата одиночными выстрелами на рас­стояние 100 м Св=21 см, Сб = 20 см (согласно табличным данным). Тогда Вв или Вб можно считать равным 7 см. Определить величинуR ₅₀[12].

Решение. R₅₀=l,76·7=12,32 см.

В этом примере при определении величины R₅₀ мы пользовались средними данными величины В, взятыми из таблиц. Чтобы определить величину R₅₀ в каждом частном случае стрельбы, исходя из располо­жения попаданий, можно поступить так:

• провести оси рассеивания по высоте и по боковому направлению;

• измерить отклонения попаданий относительно этих осей;

• найти величину среднего квадратического отклонения как по вы­соте, так и по боковому направлению;

• пользуясь зависимостью В =2/3 В₂, найти величину срединных отклонений по высоте и по боковому направлению;

• по формуле найти величину R₅₀.

Как было указано, R₅₀ = 1,76 В. Если считать, что полное рассеи­вание равно ±4 В, то R₁₀₀ будет равен (4 : 1,76)R₅₀ =2,3 R₅₀.

Если же считать, что полное рассеивание равно ±6 В, то

R₁₀₀=(6:1,76)R₅₀ =3,4 R₅₀.

Из этого следует вывод, что R₅₀ является более точной мерой, чем R₁₀₀, так как величина последней зависит от заданной степени точно­сти полной площади рассеивания.

Обычно считают, что R_l00=(2,5 : 3)R₅₀.

Таким образом, установлены зависимости между всеми мера­ми рассеивания. Эти зависимости в дальнейшем позволят решить ряд вопросов практического значения.

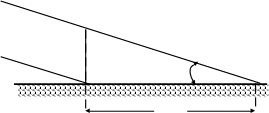
Чтобы найти соотношение между величинами рассеивания по высоте и по дальности, рассмотрим рис. 35, на котором изображены две траек­тории, проходящие на расстоянии одного срединного отклонения одна от другой. Величина АВ есть срединное отклонение по высоте (Вв), а ВС - срединное отклонение по дальности (Вд).

Без существенных погрешностей можно считать, что на небольших участках снопа рассеивания отдельные траектории параллельны между собой. Тогда между срединным отклонением по высоте и срединным от­клонением по дальности будет следующее соотношение:

Вв= Вд ·tg Θ_c, где Θ_c - угол падения.

При небольших углах падения Вв легко находится по формуле «ты­сячной» из треугольника ABC (рис. 35):

А

Вв

В Θ_с С

Вд

Рис. 35. Зависимость между Вв и Вд.

П риведенная зависимость ме­жду Вв и Вд позволит далее решать ряд задач, объясняющих не­которые особенности изменения величин рассеивания для пулеметов и минометов; позволит также выяснить законо­мерность изменения рассеивания дальности и обосновать правила выбора заряда при стрельбе с пере­менными зарядами.