1.8 Меры точности измерений - средние ошибки. Определение подходящего значения срединной ошибки

В стрелковой практике часто приходится сравнивать разные способы измерения по степени их точности. Для этого используют какую-то общую меру точности способов измерения. Такой мерой явля­ется средняя ошибка, допускаемая при том или ином методе измерения.

За среднюю ошибку принимают одну из следующих мер: или сре­динную, или среднюю арифметическую, или среднюю квадратическую ошибку.

Наиболее распространенной мерой точности является срединная ошибка, которая обозначается буквой Е.

Срединной ошибкой называется такая ошибка, которая по своей абсолютной величине больше каждой из ошибок одной половины и мень­ше каждой из ошибок другой половины всех ошибок, расположенных в ряд в возрастающем или убывающем порядке.

Исходя из этого определения, найдем срединную ошибку из 100 результатов измерений. Для этого абсолютные величины всех получен­ных ошибок расположим в возрастающем порядке в приводимой ниже таблице.

Таблица № 3.

Результаты измерений ошибок.

№	Δ	№	Δ	№	Δ	№	Δ	№	Δ
1	2	3 4	4 5	5 6	6 8	7 9	8	9 11	10
1	+ 1	21	+ 19	41	-33	61	-53	81	+ 74
2	-2	22	-20	42	+ 34	62	+ 53	82	+ 75
3	- 5	23	-20	43	-35	63	-56	83	- 78
4	- 5	24	-21	44	+ 36	64	- 56	84	- 81 ----- — \J J.
5	+ 5	25	+ 21	45	-37	65	+ 57	85	+ 82
6	- 6	26	-22	46	-37	66	-59	86	+ 86
7	+ 7	27	+ 22	47	+ 38	67	-61	87	+ 86
8	- 8	28	-23	48	+ 38	68	+ 62	88	+ 89
1	2	3	4	5	6	7	8	9	10
9	+ 8	29	-24	49	+ 39	69	-63	89	- 92
10	+8	30	+24	50	+39	70	-63	90	+98
11	+10	31	+25	51	-41	71	+63	91	+97
12	-11	32	-27	52	-41	72	+ 64	92	- 103
13	-12	33	-27	53	+ 44	73	-65	93	+ 105
14	+ 12	34	-28	54	-46	74	+ 67	94	-107
15	-13	35	+ 28	55	+ 46	75	-70	95	-112
16	+ 13	36	-29	56	+ 47	76	+ 70	96	+ 112
17	-14	37	+ 29	57	-49	77	+ 71	97	-114
18	-17	38	-31	58	+ 49	78	+ 72	98	- 117
19	+ 17	39	-31	59	-52	79	-74	99	- 121
20	+ 18	40	+ 32	60	+ 52	80	+ 74	100	+ 124

Найдем такую ошибку, которая в ряде всех ошибок занимает срединное положение. Так как мы имеем всего 100 измерений, то сре­динная ошибка будет занимать место между 50-й и 51-й ошибками. Абсолютная величина 50-й ошибки равна 39 м, а 51-й— 41 м. Срединная ошибка рассматриваемого ряда измерений равна:

м.

Действительно, ошибка величиной 40 м больше каждой ошибки пер­вой половины ряда всех ошибок и меньше каждой ошибки второй половины ряда всех ошибок.

В приведенной таблице из всех 100 ошибок 50% ошибок по своей абсолютной величине меньше найденной нами срединной ошибки. По­смотрим, сколько в этой половине положительных и сколько отрица­тельных ошибок.

Положительных ошибок, в пределах 1Е оказалось 24, т. е., приблизительно, 25% всех ошибок; отрицательных ошибок в этих пределах - 26, т. е. также около 25% всех ошибок.

Найдем число ошибок в пределах от +1Е до +2Е и выразим их в %. Ошибок от 41 до 80 м всего оказалось 33; из них положительных ошибок - 17, отрицательных - 16, т. е. примерно, по 16%.

Таким же образом определяется % ошибок в пределах от ±2Е до ±3Е и от ±3 Е до ±4 Е.

Р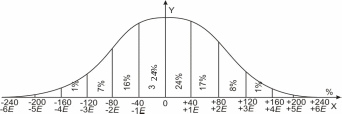 езультаты подсчетов отразим графиком - шкалой ошибок (рис. 11),

Рис. 11. Шкала ошибок из опыта.

Если взять достаточно большое число ошибок, при котором можно считать, что частота события равна вероятности его появления, тогда частота появления ошибок в пределах одной Е будет выражена в % на рис. 12. Этот график представляет собой численное выражение нормального закона ошибок, так как он показывает численную зависимость между величинами ошибок, выраженными в Е, и вероятностями получе­ния их в определенных пределах.

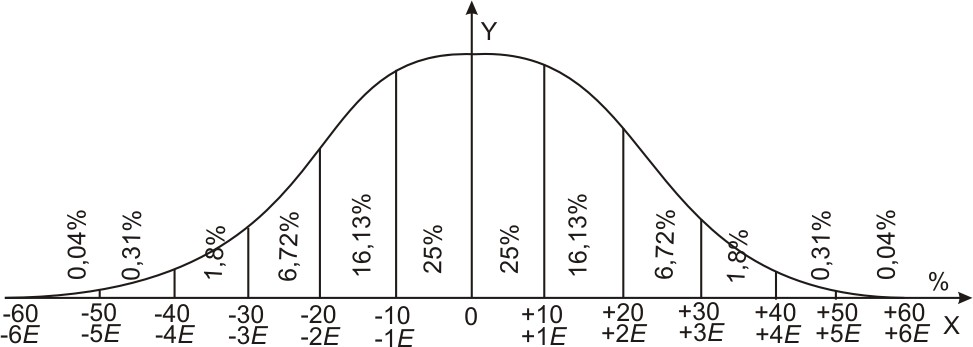
Рис. 12. Численное выражение нормального закона ошибок.

Так, например, на основании полученного графика мы можем ска­зать, что вероятность получения ошибки в пределах величин:

• одной срединной ошибки равна 25% +25%= 50%;

• двух срединных ошибок равна 16,13%+25%+25%+16,13% = 82,26%.

На основании данных рис. 12 можно сказать, что ошибки измере­ния по своей величине могут достигать до ±5Е и даже до ±6Е. Но из этого же рисунка видно, что вероятность получения таких больших ошибок очень невелика. На самом деле, вероятность получения ошибки бо­лее 4Е равна 2·(0,31% +0,04%) =0,70%. Это означает, что из 1000 из­мерений только в 7 случаях ошибка может быть больше 4Е.

На основании этого с целью упрощения расчетов численное выра­жение нормального закона ошибок обычно округляют, представляя его в виде шкалы (рис. 13), которую называют шкалой ошибок. В этом случае практическим пределом ошибки для любого способа измерения при­нимают предел ± 4Е.

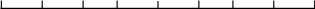0,02 0,07 0,16 0,25 0,25 0,16 0,07 0,02

-4Е –3Е –2Е –1Е 0 +1Е +2Е +3Е +4Е

Рис. 13. Шкала ошибок.

Шкала ошибок на рис. 13 составлена в целых долях срединной ошибки Е. Такую шкалу можно составить с любой точностью - в любых долях Е. На рис. 14 дана шкала ошибок, которая позволяет определить вероятность получения ошибки в пределах с точностью до 1/2 Е и до 1/4 Е. Так, например, вероятность получить ошибку в пределах ± 1/2Е равна 0,13+0,13 =0,26 или 26%; в пределах ±1 Е равна (0,25+ 0,051)2 =0,602 или 60,2%; в пределах от – -l Е до + 1 Е равна 0,09 + 0,25 + 0,067 = 0,407 или 40,7%; в пределах от

+ Е до+1 Е равна 0,12 + 0,09 + 0,037 = 0,247 или 24,7%.

0,02				0,07				0,16				0,25				0,25				0,16				0,07				0,02
0,005		0,015		0,03		0,04		0,07		0,09		0,12		0,13		0,13		0,12		0,09		0,07		0,04		0,03		0,015		0,005
0,002	0,004	0,005	0,008	0,011	0,014	0,019	0,024	0,031	0,037	0,044	0,051	0,056	0,064	0,066	0,067	0,067	0,066	0,064	0,056	0,051	0,044	0,037	0,031	0,024	0,019	0,014	0,011	0,008	0,005	0,004	0,002

-4Е –3Е –2Е –1Е 0 +1Е +2Е +3Е +4Е

Рис. 14. Шкала ошибок с точностью до 1/4 Е.

При расчетах, требующих большой точности, пользуются шкалой ошибок, составленной до 0,01 Е. Такая шкала имеет вид таблицы, где вероятность получения ошибки в пределах от 0 до ± Вдается как Ф (В), т. е. как функция того или иного предела, выраженного в Е.

Пользование этой таблицей покажем на примерах.

Положим, что истинное расстояние до цели равно 800 м. Наблюдатель, измеряя это расстояние глазомером, допускает какую-то ошибку. Срединная ошибка измерения равна 10% (см. табл. № 4), что в данном случае состав­ляет 80 м.

Таблица № 4.

Процентный размер ошибок

№ по пор.	Наименование ошибок	величина срединной ошибки
1 2 3 4 5 6 7	Ошибка в определении расстояния до цели: глазомером……………………………………. промером местности шагами………………... по карте……………………………………….. Ошибка в определении скорости ветра (без приборов)…… Ошибка в определении скорости цели (без приборов)……………. Ошибка в определении температуры воздуха (без приборов)……. Ошибка приведения оружия к нормальному бою…………………. Ошибка наводки оружия: лёжа с руки…………………………………………………… с колена без упора…………………………………………… на ходу с короткой остановки………………………………. Ошибка в определении курсового угла цели……………………….	10%Д 4%Д 5%Д 1,5м/сек 20% ц 5°С 0,3 тыс. 0,4 тыс. 0,8 тыс. 2,0 тыс. 0,1 радиана

1 Определить вероятность получения ошибки в пределах ±100 м (рис. 15). Решение В =100:80= ±1,25Е.

Вероятность получения ошибки в заданных пределах

Р =Ф(В)=Ф(1,25Е)=0,601 или 60,1%.

Рис. 15. Вероятность получения ошибок в пределах ±1,25Е.

2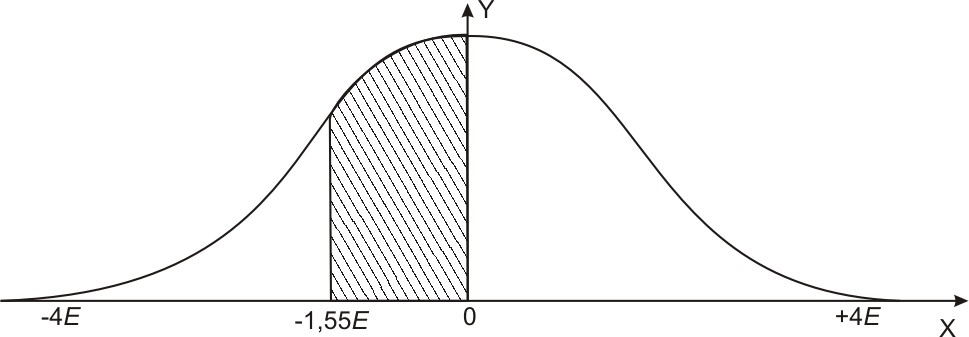 . Определить вероятность получения отрицательной ошибки в преде­лах от 0 до 124 м (рис. 16).

Рис. 16. Вероятность получения ошибок в пределах от 0 до – 1,55 Е.

Решение В= 124:80=1,55 Е

и ли 35,2%.

Повторяя измерения какой-либо величины одним и тем же спосо­бом, мы получаем разные результаты с разными по величине и знаку ошибками. Положим, что мы имеем ряд измерений и нам требуется оп­ределить ошибку каждого результата измерения. Для этого надо знать истинное значение измеряемой величины. Но так как это невозможно, нужно найти такое значение, которое можно было бы считать наиболее подходящим к истинному значению измеряемой величины. Данному ус­ловию отвечает среднее арифметическое из всех отдельных результатов измерений, т. е. средний результат.

Например, 10 человек измеряли глазомерным способом расстояние до одного и того же местного предмета. При этом были получены сле­дующие результаты измерений: 930, 1150, 1071, 730, 1050, 955, 760, 1260, 839, 1015 м.

( Средний результат 976 м считаем наиболее подходящим значением измеряемой величины, т. е. принимаем его за истинное значение. Теперь можно определить ошибки каждого результата измерений, как разность между результатами отдельных измерений и найденным подходящим значением измеряемой величины. Мы получим: -46, + 174, +95, -246, +74, -21, -216, +284, -137, +39 м). Определить средний результат Д_ср.

Р асположим абсолютные значения этих ошибок в возрастающем (можно в убывающем) порядке: 21, 39, 46, 74, 95, 137, 174, 216, 246, 284 (м). Срединная ошибка этого ряда будет равна:

Однако так находить срединную ошибку можно только при большом количестве измерений. При малом числе измерений срединную ошибку определяют одним из следующих двух способов: или по величине сред­ней арифметической ошибки, или по величине средней квадратической ошибки. Для этого нужно знать, как определяются, величины названных ошибок и какие существуют численные зависимости между этими ошиб­ками и срединной ошибкой.

Средняя арифметическая ошибка (E₁) равна сумме абсолютных значений величин ошибок, деленной на число ошибок, т. е.

П о условию предыдущего примера, где было произведено 10 изме­рений и получено 10 ошибок, средняя арифметическая ошибка равна:

Между срединной ошибкой (Е) и средней арифметической ошибкой (E₁) существует следующая численная зависимость: срединная ошибка равна 5/6 средней арифметической ошибки Е=5/6Е₁

(точнее Е=0,84535Е₁).

На основании этого можно найти величину срединной ошибки, если известна величина средней арифметической ошибки.

По условию нашего примера срединная ошибка

E= м.

Средняя квадратическая ошибка (Е₂) равна квадратному корню из

с уммы квадратов абсолютных значений величин ошибок, деленной на число ошибок без одной, т. е.

По условию предыдущего примера из 10 измерений средняя квадра­тическая ошибка равна:

М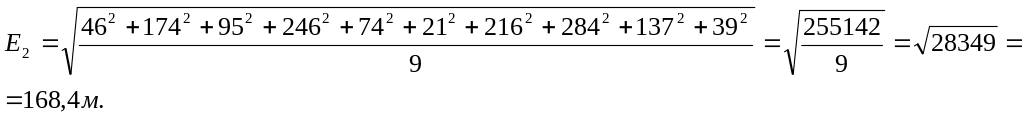 ежду срединной ошибкой (Е) и средней квадратической ошибкой (E₂) установлена следующая зависимость: срединная ошибка равна 2/3 средней квадратической ошибки

(точнее, Е = 0,67449 Е₂).

Н а основании этой зависимости найдем величину срединной ошибки, если известна величина средней квадратической ошибки по условию на­шего примера:

В приведенных примерах величина срединной ошибки Е, найденная построением ошибок в ряд (116 м), незначительно отличается от вели­чины срединной ошибки, найденной по средней арифметической (111 м), и от величины Е, найденной по средней квадратической ошибке (112 м). Однако теория стрельбы установила, что наиболее точно срединная ошибка может быть определена по средней квадратической ошибке.

Рассмотрим пример, на котором покажем, что при небольшом ко­личестве измерений срединную ошибку необходимо определять только через среднюю квадратическую.

Два офицера при троекратном измерении расстояния по карте коман­дирской линейкой допустили следующие ошибки в миллиметрах: пер­вый измерявший - 1, 3, 5; второй измерявший - 2, 3, 4. Кто из них рабо­тал точнее?

По характеру допущенных ошибок можно предположить, что точнее измерял второй.

П одсчитаем среднюю ошибку каждого измерявшего, взяв за нее среднюю арифметическую величину. Тогда получается, что средняя арифметическая ошибка первого измерявшего

и у второго

т. е. они работали одинаково точно. Однако сам вид ошибок показывает нам, что точнее работал второй измерявший. Проверим это по средней квадратической ошибке, которая являет­ся более высокой мерой точности при небольшом числе измерений. Най­дем среднюю квадратическую ошибку первого и второго измерявшего:

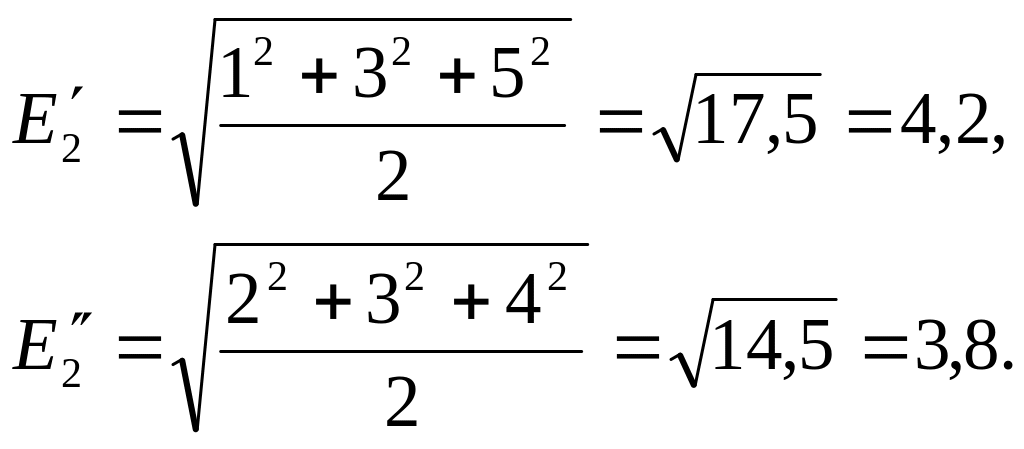
Теперь мы подтвердили свое предположение о том, что второй изме­рявший работал точнее: у него средняя квадратическая ошибка меньше, чем у первого. Этот расчет убеждает нас и в том, что средняя квадрати­ческая ошибка оказывается более высокой мерой точности, чем средняя арифметическая.

Если же мы в приведенном примере сравним допущенные измеряв­шими срединные ошибки, находя их по положению в ряду, то мы не придем к правильному решению: срединные ошибки оказываются равными. Получается, что точность работы измерявших одинакова. Это, как мы уже показали, неверно и произошло потому, что при малом количестве измерений срединную ошибку нельзя находить построением ошибок в ряд.

Итак, при небольшом числе измерений срединную ошибку следует находить по средней квадратической ошибке, зная, что Е = Е₂.

Тогда в нашем примере для первого измерявшего Е'= 4,2=2,8, для второго измерявшего Е"= ·3,8=2,53, т. е. он работал точнее.

Таким образом, при малом количестве измерений за подходящее значение срединной ошибки следует принимать срединную ошибку, най­денную по средней квадратической.

Вернемся к рассмотренному ранее примеру с 10-ю измерениями. Мы нашли ошибку каждого результата измерения, после чего определили подходящее значение срединной ошибки различными способами:

- по месту в ряде абсолютных значений ошибок срединная ошибка оказалась равна Е=116 м;

- по средней квадратической ошибке срединная ошибка равна 112м.

И здесь легко убедиться в недостаточной точности первого способа. Действительно, достаточно добавить к нашему ряду еще одно (11-е) из­мерение, как искомая величина Е резко изменится (вместо 116 м станет 137 м или 95 м).

Чтобы убедиться в преимуществе второго способа, применим к нему те же испытания, что и к первому способу, т. е. посмотрим, как изменит­ся искомая величина Е, если к имеющимся ошибкам 10-ти измерений добавить ошибку 11-го измерения. Пусть в одном случае эта ошибка равна 140 м (больше 137 м), а в другом - 80 м (меньше 95 м).

При 11-ти измерениях с добавлением ошибки 140 м срединная ошибка Е, найденная по средней квадратической, будет равняться 110м.

При 11-ти измерениях с добавлением ошибки 80 м срединная ошибка Е, найденная по средней квадратической, будет составлять 108 м.

Как видим, добавочное измерение незначительно изменяет сужде­ние о величине срединной ошибки, если ее определять по средней квадратической ошибке.

Таким образом, практически для определения подходящего значе­ния срединной ошибки следует применять способ определения срединной ошибки по средней квадратической, пользуясь зависимостью

П ример. Определить срединную ошибку измерения дальности до цели, если получены следующие результаты в м: 360, 400, 450, 390.

Решение: