Определение:

Верхняя опорная прямая для набора точек на плоскости включает минимум одну точку из , и все точки из лежат ниже или на этой линии.

Сейчас допустим, что является верхней опорной прямой для набора и проходит через точку èç . Предположим, что не является верхним мостиком для è , также допустим, что является отрезком, где . Если наклон не меньше, чем наклон , тогда легко увидеть, что этот отрезок не может быть включен в верхний мостик для è . В частности, точка не может принадлежать верхнему мостику. Подобным образом, если является верхней опорной прямой набора , проходящей через точку èç , полагаем, что не принадлежит верхнему мостику для è , è является отрезком, где . Если наклон не больше, чем наклон , тогда отрезок не может находиться в этом верхнем мостике для è . В частности, точка не может принадлежать верхнему мостику.

Это ключевое наблюдение предлагает нам следующий алгоритм решения описанной задачи.

Алгоритм ‘Верхний мостик’ (s,l)

Входные данные: Набор из точек на плоскости и вертикальная линия , разделяющая на левое и правое подмножества.

Выходные данные: Верхний мостик для множеств и .

НАЧАЛО

1. Произвольно образуем пары точек из :

;

2. Допустим, что наклон для сегмента есть .

Используем алгоритм Поиска Медианы для нахождения пары , такой, что наклон есть медиана для;

3. Конструируем верхнюю опорную прямую, с наклоном : Вычерчиваем линию с наклоном 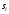через каждую точку в . Далее берем линию, которая имеет самую старшую координату по оси .

4. Если 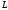проходит через точки и в и в , тогда является верхним мостиком, который мы хотели построить, значит, мы останавливаемся и возврат. Иначе, делаем следующий шаг.

5. Если проходит только через точки в , тогда просматриваем список из пар , который мы создали на Шаге 1. Если наклон сегмента не меньше, чем наклон этой опорной прямой , то отбрасываем точку .

6. Если проходит только через точки из, тогда просматривается список пар , полученный нами на Шаге 1. Если наклон сегмента не больше, чем наклон этой опорной прямой, то отбрасывается точка .

6. Пусть будет набором оставшихся точек из , рекурсивно вызываем

Верхний мостик.

КОНЕЦ.

Корректность Алгоритма ‘Верхний мостик’ может быть доказана с помощью рассуждения, предшествующего алгоритму: мы никогда не удаляем точки из верхнего мостика. Теперь мы должны обсудить временную сложность этого алгоритма. Шаг1, Шаг3 и Шаг4 могут быть явно сделаны за время . Шаг2 может быть выполнен за линейное время, используемое алгоритмом Нахождения Медианы, описываемом ранее. Теперь мы должны обсудить, как много точек передается при рекурсивном вызове алгоритма на Шаге7. Т.к. наклон из является медианой среди наклонов для отрезков , от 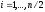, то, если Шаг5 выполнен, то по меньшей мере половина отрезков имеет наклон не меньший чем . Таким образом соответствующие точки отбрасывается. Следовательно, как минимум точек из будет отброшена. Подобным же образом, если Шаг6 выполнен, также минимум точек отбрасывается. Следовательно максимум 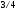точек из передана при рекурсивном вызове на Шаге7. Можем оценить временную сложность Алгоритма ‘Верхний мостик’, для которой мы имеем следующее рекуррентное соотношение:

Просто показать, что . Следовательно, Алгоритма ‘Верхний мостик’ выполняется за линейное время.

С такой подготовкой теперь можно представить следующий алгоритм Кирпатрика – Сайделя:

Алгоритм Кирпатрика – Сайделя:

Входные данные: Множество из точек на плоскости

Выходные данные: Выпуклая оболочка над

НАЧАЛО:

1. Определим и как точки из , которые имеют минимальную и максимальную -координаты соответственно, определим линию через и как.

2. Разобьем множество на два подмножества и, т.ч. является набором точек из , лежащих выше линии , и является набором точек из , лежащих ниже линии .

3. Вызов Верхняя_Оболочка ;

4. Вызов Нижняя_Оболочка;

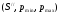КОНЕЦ.

Шаг1 и Шаг2 алгоритма Кирпатрика – Сайделя могут быть выполнены за линейное время. Функции Верхняя_Оболочка è Нижняя_Оболочка подобны. Мы обсудим только функцию Верхняя_Оболочка, она следующая:

Алгоритм Верхняя_Оболочка(S, p_min, p_max)

Входные данные: Множество èç точек на плоскости, которое лежит выше, чем линия, проходящая через è , которые тоже точки из .

Выходные данные: Верхняя оболочка над .

НАЧАЛО

1. Íàø Алгоритм Поиск Медианы ищет вертикальную линию , которая разделяет множество на два эквивалентных по размеру подмножества è .

2. Вызов Верхний_Мостик конструирует верхний мостик äëÿ è , ãäå лежит в è лежит в .

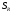3. Определим , как множество из точек в , которое лежит выше линии, проходящей через è , и определим , как множество точек из , которые лежат выше линии, проходящей через è .

4. Рекурсивно вызываем Верхняя_Оболочка è Верхняя_Оболочка

5. Сливаем результаты Шага4 с собственно верхним мостиком .

КОНЕЦ.

Теперь обсудим временную сложность Алгоритма ‘Верхняя Оболочка’.

Пусть точек из множества принадлежат этой выпуклой оболочке .

Допустим, является временной сложностью этого алгоритма. Шаг 1 потребует время при работе Алгоритма Поиск Медианы. Шаг 2 потребует время по нашему анализу Алгоритма ‘Верхний Мостик’. Шаг3 и Шаг 5 могут быть явно сделаны за время . Теперь допустим, что вершин из входят во множество , è вершин из входят во множество 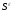. Тогда рекурсивные вызовы на Шаге4 потребуют время максимум , ãäå , т.к. легко увидеть, что è . Следовательно, мы имеем следующее рекуррентное соотношение:

Мы можем доказать по индукции по , ÷òî 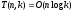. Детали доказательства здесь опускаются.

Таким образом, Алгоритм Кирпатрика – Сайделя выполняется за время. Когда невелико, Алгоритм Кирпатрика – Сайделя íå õóæå, ÷åì Алгоритм Джарвиса, который имеет временную сложность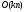 (даже лучше), а если – большое, то является, однако не хуже, чем Просмотр Грэхема.

В заключение, мы кратко обсудим отличие между Алгоритмами Слияние Оболочек, Быстрая Оболочка и Алгоритмом Кирпатрика-Сайделя. Алгоритм Кирпатрика-Сайделя имеет преимущество над обоими (Слияние Оболочек, Быстрая Оболочка) алгоритмами. Он разделяет заданные множества равномерно, подобно Быстрой Оболочке. Временная сложность Слияния Оболочек имеет коэффициент вместо , потому что разделен на два рекурсивных вызова, что позволяет представить многие точки из выпуклых оболочек двух подмножеств, не принадлежащие выпуклой оболочке исходного множества.

К сожалению, в Быстрой Оболочке медиана заданного множества может не быть вершиной оболочки, следовательно, алгоритм не будет работать, если мы просто заменим следующую точку в алгоритме на медиану.

^#70 Нарисовать выпуклую оболочку

Рисуется выпуклая оболочка. При нажатой кнопке оболочка будет автоматически перерисовываться при изменении множества точек.

^#71 Пауза

Остановка автоматического пошагового режима.

^#72 Cтоп

Выход из пошагового режима.

^#73 Перемотка

Автоматический вывод шагов алгоритма в обратном порядке.

^#74 Демо

Автоматический вывод шагов алгоритма.

^#75 Следующий шаг

Визуализация следующего шага алгоритма.

^#76 Предыдущий шаг

Визуализация предыдущего шага алгоритма.

^#77 Помощь

Помощь по выбранному элементу интерфейса.

^#78 Добавить точку

При выборе данного пункта меню вызывается диалоговое окно в котором можно задать координаты добавляемой точки.

{bmc p_add.bmp}

^#79 Удалиь точку

При выборе данного пункта меню вызывается диалоговое окно в котором можно задать номер удаляемой точки.

{bmc p_del.bmp}

^#80 Редактировать точку

При выборе данного пункта меню вызывается диалоговое окно в котором можно задать номер редактируемой точки и изменить её координаты.

{bmc p_edt.bmp}

^#81 Случайная генерация точек

При выборе данного пункта меню вызывается диалоговое окно, в котором можно задать количество генерируемых точек, а также задать область генерации точек. Область может быть задана пользователем (координаты верхнего левого и нижнего правого угла прямоугольника в котором будет производится генерация точек) либо точки разбрасываются по всему рабочему пространству.

{bmc p_rnd.bmp}

^#82 Установка задержки

При выборе данного пункта меню вызывается диалоговое окно, в котором можно задать задержку (в секундах) между шагами алгоритма в автоматическом пошаговом режиме.

{bmc setdelay.bmp}

1^# main_index

2^# menu_file

3^K files: managing

4^$ File menu commands

5^# menu_edit

6^# menu_view

7^# points_edit

8^# setshowch

9^# setings

10^# menu_window

11^# menu_window

12^# menu_help

13^# HID_FILE_NEW

14^K files: managing

15^$ File New command

16^# HID_FILE_OPEN

17^K files: managing

18^$ File Open command

19^# HID_FILE_CLOSE

20^K files: managing

21^$ File Close command

22^# HID_FILE_SAVE

23^K files: managing

24^$ File Save command

25^# HID_FILE_SAVE_AS

26^K files: managing

27^$ File Save As command

28^# HID_APP_EXIT

29^K exit

30^$ File Exit command

31^# HID_EDIT_CUT

32^# HID_EDIT_COPY

33^# HID_EDIT_PASTE

34^# HID_VIEW_TOOLBAR

35^K toolbar

36^$ View Toolbar command

37^# AFX_HIDW_TOOLBAR

38^K toolbar

39^$ toolbar

40^# HID_VIEW_STATUS_BAR

41^K status bar

42^$ View Status Bar Command

43^# AFX_HIDW_STATUS_BAR

44^K status bar

45^$ status bar

46^# HID_WINDOW_NEW

47^# HID_WINDOW_CASCADE

48^# HID_WINDOW_TILE

49^# HID_WINDOW_ARRANGE

50^# HID_WINDOW_ALL

51^# HID_APP_ABOUT

52^# HIDR_DOC1TYPE

53^# HID_HT_NOWHERE

54^# AFX_HIDP_default

55^# HIDD_ADD_DIALOG

56^# HID_OPEN_TEXT

57^# HID_SAVE_TEXT

58^# HID_POINTS_DELETE

59^# HID_1_1

60^# HID_BEST_FIT

61^# HID_ZOOM_IN

62^# HID_ZOOM_OUT

63^# HID_SHOW_POINTS

64^# HID_SHOW_TEXT

65^# HID_HELP_INDEX

66^# HIDD_DELETE_DIALOG

67^# HIDD_EDIT_DIALOG

68^# HIDD_RANDOM_DIALOG

69^# algorithm

70^# HID_SHOW_DIAG

71^# HID_PAUSE

72^# HID_STOP

73^# HID_BACK

74^# HID_DEMO

75# HID_STEP_BY_STEP_TOOLBAR

76^# HID_REWIND

77^# HID_CONTEXT_HELP

78^# HID_POINTS_ADD

79^# HID_POINTS_DEL

80^# HID_POINTS_EDT

81^# HID_POINTS_RND

82^# HID_STEP_BY_STEP