
- •Лабораторная работа по теме: методы поиска
- •Краткие сведения из теории
- •1. Линейный (последовательный) поиск
- •2. Быстрый последовательный список
- •3. Дихотомический (бинарный) поиск
- •4. Интерполяционный поиск
- •5. Сравнение рассмотренных методов
- •Контрольные вопросы
- •Методические указания
- •Содержание отчета
- •Варианты индивидуальных заданий
4. Интерполяционный поиск
Рассмотрим еще один метод, имеющий хорошую теоретическую сложность. Как и предыдущий, этот метод предполагает, что множество хранится в массиве и массив отсортирован. Как и предыдущий метод, этот на каждом шаге своей работы сокращает область поиска. Но в отличие от предыдущего метода проба берется не в середине рассматриваемой области.
Пусть имеется область поиска (l, r). Предположим, что элементы множества – целые числа, возрастающие в арифметической прогрессии. Тогда искомый элемент должен находится в массиве (если он вообще там есть) под индексом (это следует из свойств арифметической прогрессии). В этом элементе и будем брать пробу.
l := 1; r := n;
while (l<>r) do
begin
m := l+(r-l)*(Key-A[l])/(A[r]-A[l]);
if Key>A[m] then l := m+1 else r := m;
end;
if A[l]=Key then <элемент найден> else <элемент не найден>;
Мы сделали очень большое допущение, предположив, что элементы массива представляют собой возрастающую арифметическую прогрессию. В реальности такая ситуация встречается редко. Но этот метод хорошо работает для любых пусть не идеально, но более-менее равномерно распределенных данных. Если же мы имеем дело с неравномерно распределенными данными, то интерполяционный поиск может увеличить число шагов по сравнению с дихотомическим поиском. Теоретическая сложность интерполяционного поиска – T(log(log(n))). Это, конечно, лучше, чем сложность дихотомического поиска, но эти преимущества становятся достаточно заметными лишь при очень больших значениях n. Практически на всех реальных n разница между дихотомическим и интерполяционным поиском по скорости не существенна.
Добавление и удаление можно реализовать так же, как при дихотомическом поиске. К этим операциям предъявляется то же требование: они должны сохранять массива отсортированным.
5. Сравнение рассмотренных методов
Приведенная таблица поможет сравнить методы друг с другом.
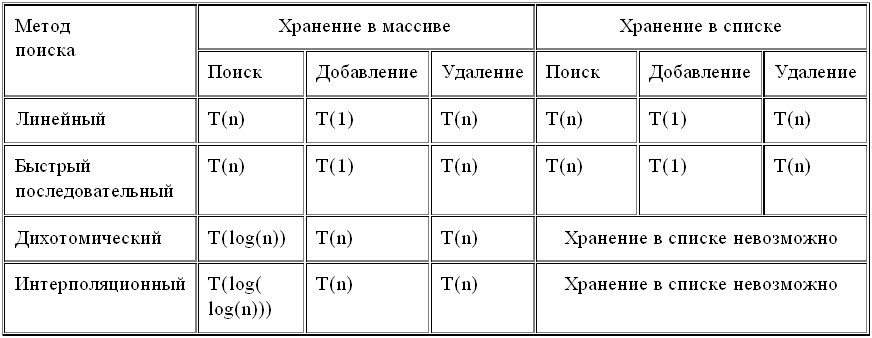
Быстрый последовательный поиск с хранением множества в списке (при списковом хранении удаление будет выполняться в среднем в 2 раза быстрее) лучше применять в случаях, когда операции добавления/удаления будут выполняться чаще операции поиска. В этом случае лучше проиграть на поиске, но выиграть на добавлении и удалении.
Для случая же когда будут преобладать операции поиска, лучшим выбором является дихотомический поиск. Почему не интерполяционный? Частично об этом уже сказано в разделе 4. Интерполяционный поиск предполагает, что данные распределены равномерно. В противном случае, возможно, замедление работы по сравнению с дихотомическим поиском. Да и дихотомический поиск работает достаточно быстро. Чтобы найти искомый элемент (или выяснить, что его нет) среди 1 млрд. элементов отсортированного множества, бинарному поиску хватит около 30 сравнений.
Контрольные вопросы
Почему последний из разобранных методов поиска называется интерполяционным?
Почему при хранении в списке невозможно воспользоваться дихотомическим и интерполяционным поиском?
Почему операция удаления при хранении множества в списке в среднем в 2 раза медленнее, чем при хранении в неотсортированном массиве?
