Задача:

Заданы два набора и точек на плоскости, так, что есть такая вертикальная линия , что - слева от и – справа от . Как найти верхний мостик между и , т.е. линию, проходящую через точку в и точку в таким образом, что все точки из и лежат ниже этой линии?

В алгоритме ‘Слияния оболочек ‘, мы знаем, что когда выпуклая оболочка обоих наборов и известна, верхний мостик может быть сконструирован за линейное время при подъеме отрезка между и до тех пор, пока уже больше не сможем поднимать отрезок. Однако построение выпуклой оболочки над и само требует времени , которое чересчур велико для нас, т.к. мы ожидаем от алгоритма линейного времени решения задачи.

В решении вышеописанной задачи использована технология Отсечения и Поиска. Главная идея касается поиска “подходящих” линий за время , линий, которые позволяют отбросить постоянную долю точек, как кандидатов на попадание в мостик. Мы используем рекурсию относительно оставшихся точек.

Определение:

Верхняя опорная прямая для набора точек на плоскости включает минимум одну точку из , и все точки из лежат ниже или на этой линии.

Сейчас допустим, что является верхней опорной прямой для набора и проходит через точку из . Предположим, что не является верхним мостиком для и , также допустим, что является отрезком, где . Если наклон не меньше, чем наклон , тогда легко увидеть, что этот отрезок не может быть включен в верхний мостик для и . В частности, точка не может принадлежать верхнему мостику. Подобным образом, если является верхней опорной прямой набора , проходящей через точку из , полагаем, что не принадлежит верхнему мостику для и , и является отрезком, где . Если наклон не больше, чем наклон , тогда отрезок не может находиться в этом верхнем мостике для и . В частности, точка не может принадлежать верхнему мостику.

Это ключевое наблюдение предлагает нам следующий алгоритм решения описанной задачи.

Алгоритм ‘Верхний мостик’ (s,l)

Входные данные: Набор из точек на плоскости и вертикальная линия , разделяющая на левое и правое подмножества.

Выходные данные: Верхний мостик для множеств и .

НАЧАЛО

1. Произвольно образуем пары точек из :

;

2. Допустим, что наклон для сегмента есть .

Используем алгоритм Поиска Медианы для нахождения пары , такой, что наклон есть медиана для;

3. Конструируем верхнюю опорную прямую, с наклоном : Вычерчиваем линию с наклоном через каждую точку в . Далее берем линию, которая имеет самую старшую координату по оси (максимальный коэффициент b, имея ввиду представление прямой уравнением y=s_l*x+b ).

4. Если проходит через точки и в и в , тогда 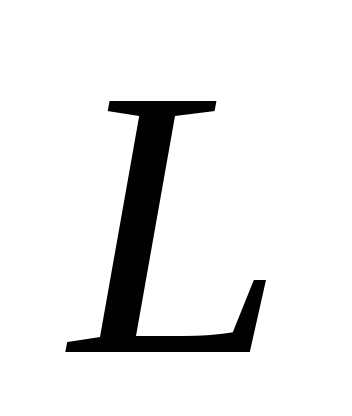является верхним мостиком, который мы хотели построить, значит, мы останавливаемся и возврат. Иначе, делаем следующий шаг.

5. Если проходит только через точки в , тогда просматриваем список из пар , который мы создали на Шаге 1. Если наклон сегмента не меньше, чем наклон этой опорной прямой , то отбрасываем точку .

6. Если проходит только через точки из, тогда просматривается список пар , полученный нами на Шаге 1. Если наклон сегмента не больше, чем наклон этой опорной прямой, то отбрасывается точка .

6. Пусть будет набором оставшихся точек из , рекурсивно вызываем

Верхний мостик.

КОНЕЦ.

Корректность Алгоритма ‘Верхний мостик’ может быть доказана с помощью рассуждения, предшествующего алгоритму: мы никогда не удаляем точки из верхнего мостика. Теперь мы должны обсудить временную сложность этого алгоритма. Шаг1, Шаг3 и Шаг4 могут быть явно сделаны за время . Шаг2 может быть выполнен за линейное время, используемое алгоритмом Нахождения Медианы, описываемом ранее. Теперь мы должны обсудить, как много точек передается при рекурсивном вызове алгоритма на Шаге7. Т.к. наклон из является медианой среди наклонов для отрезков , от , то, если Шаг5 выполнен, то по меньшей мере половина отрезков имеет наклон не меньший чем . Таким образом соответствующие точки отбрасывается. Следовательно, как минимум точек из будет отброшена. Подобным же образом, если Шаг6 выполнен, также минимум точек отбрасывается. Следовательно максимум точек из передана при рекурсивном вызове на Шаге7. Можем оценить временную сложность Алгоритма ‘Верхний мостик’, для которой мы имеем следующее рекуррентное соотношение:

Просто показать, что . Следовательно, Алгоритма ‘Верхний мостик’ выполняется за линейное время.

С такой подготовкой теперь можно представить следующий алгоритм Киркпатрика – Сайделя:

Алгоритм Киркпатрика – Сайделя:

Входные данные: Множество из точек на плоскости

Выходные данные: Выпуклая оболочка над

НАЧАЛО:

1. Определим и как точки из , которые имеют минимальную и максимальную -координаты соответственно, определим линию через 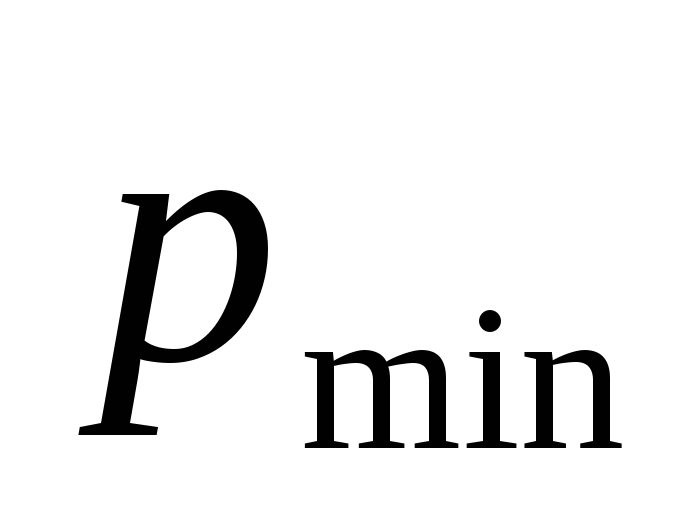и как.

2. Разобьем множество на два подмножества и, т.ч. является набором точек из , лежащих выше линии 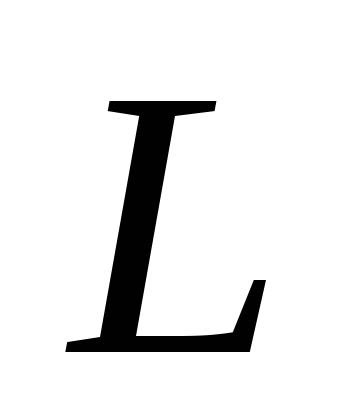, и является набором точек из , лежащих ниже линии .

3. Вызов Верхняя_Оболочка ;

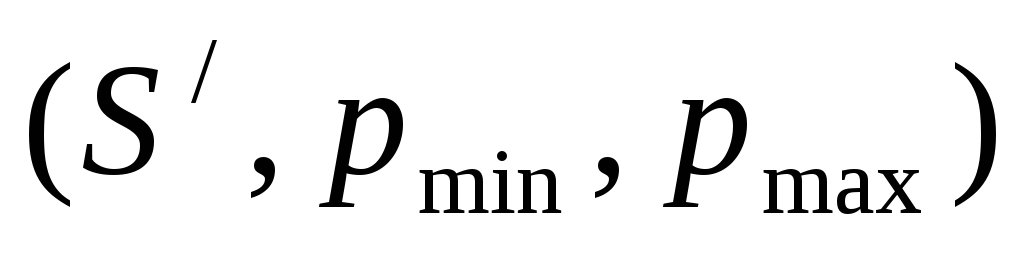4. Вызов Нижняя_Оболочка;

КОНЕЦ.

Шаг1 и Шаг2 алгоритма Киркпатрика – Сайделя могут быть выполнены за линейное время. Функции Верхняя_Оболочка и Нижняя_Оболочка подобны. Мы обсудим только функцию Верхняя_Оболочка, она следующая:

Алгоритм Верхняя_Оболочка(S, p_min, p_max)

Входные данные: Множество из точек на плоскости, которое лежит выше, чем линия, проходящая через и , которые тоже точки из .

Выходные данные: Верхняя оболочка над .

НАЧАЛО

1. Наш Алгоритм Поиск Медианы ищет вертикальную линию , которая разделяет множество на два эквивалентных по размеру подмножества и .

2. Вызов Верхний_Мостик конструирует верхний мостик для и , где лежит в и лежит в .

3. Определим , как множество из точек в , которое лежит выше линии, проходящей через и , и определим , как множество точек из , которые лежат выше линии, проходящей через и .

4. Рекурсивно вызываем Верхняя_Оболочка и

Верхняя_Оболочка

5. Сливаем результаты Шага4 с собственно верхним мостиком .

КОНЕЦ.

Теперь обсудим временную сложность Алгоритма ‘Верхняя Оболочка’.

Пусть точек из множества принадлежат этой выпуклой оболочке .

Допустим, является временной сложностью этого алгоритма. Шаг 1 потребует время при работе Алгоритма Поиск Медианы. Шаг 2 потребует время по нашему анализу Алгоритма ‘Верхний Мостик’. Шаг3 и Шаг 5 могут быть явно сделаны за время . Теперь допустим, что вершин из входят во множество , и вершин из входят во множество . Тогда рекурсивные вызовы на Шаге4 потребуют время максимум , где , т.к. легко увидеть, что и . Следовательно, мы имеем следующее рекуррентное соотношение:

Мы можем доказать по индукции по , что . Детали доказательства здесь опускаются.

Таким образом, Алгоритм Киркпатрика – Сайделя выполняется за время. Когда невелико, Алгоритм Киркпатрика – Сайделя не хуже, чем Алгоритм Джарвиса, который имеет временную сложность (даже лучше), а если – большое, то является, однако не хуже, чем Просмотр Грэхема.

В заключение, мы кратко обсудим отличие между Алгоритмами Слияние Оболочек, Быстрая Оболочка и Алгоритмом Киркпатрика-Сайделя. Алгоритм Киркпатрика-Сайделя имеет преимущество над обоими (Слияние Оболочек, Быстрая Оболочка) алгоритмами. Он разделяет заданные множества равномерно, подобно Быстрой Оболочке. Временная сложность Слияния Оболочек имеет коэффициент вместо , потому что разделен на два рекурсивных вызова, что позволяет представить многие точки из выпуклых оболочек двух подмножеств, не принадлежащие выпуклой оболочке исходного множества.

К сожалению, в Быстрой Оболочке медиана заданного множества может не быть вершиной оболочки, следовательно, алгоритм не будет работать, если мы просто заменим следующую точку в алгоритме на медиану.

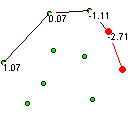
Пример работы Алгоритма.