
Алгоритм построения выпуклой оболочки (Киркпатрика – Сайделя).
Оригинал см. в гл. 6 в файле geo.pdf
Построение
выпуклой оболочки конечного множества
точек (особенно в случае точек на
плоскости) довольно широко и глубоко
исследовано и имеет целый ряд геометрических
приложений. Известно, что нижняя оценка
нахождения упорядоченной границы
выпуклой оболочки n
точек на
плоскости составляет
![]() ,
и существуют алгоритмы ее построения
за время
,
и существуют алгоритмы ее построения
за время
![]() при памяти
при памяти
![]() с использованием только арифметических
операций. Известен алгоритм, интересный
с точки зрения его быстродействия
(статья D.G.Kirpatrick
& R.Seidel
“The
ultimate
planar
convex
hull
algorithm”
(SIAM Journal on Computing, 15(2) 1986)). Его сложность
составляет
с использованием только арифметических
операций. Известен алгоритм, интересный
с точки зрения его быстродействия
(статья D.G.Kirpatrick
& R.Seidel
“The
ultimate
planar
convex
hull
algorithm”
(SIAM Journal on Computing, 15(2) 1986)). Его сложность
составляет
![]() ,
а значит, он асимптотически оптимален.
Ниже приводится перевод фрагмента
упомянутой статьи:
,
а значит, он асимптотически оптимален.
Ниже приводится перевод фрагмента
упомянутой статьи:
Отсечение
и поиск - техника, используемая для
отыскания медианы по Блуму, Флойду,
Пратту и Тарьяну. Техника, примененная
к поиску медианы, выделяет постоянную
долю чисел на каждой итерации цикла.
Решение рекуррентного уравнения дает
нам время алгоритма поиска медианы![]() .
.
При поиске медианы в списке, мы сначала обобщим проблему.
Мы
обсудим проблему поиска
![]() минимальных чисел из списка
минимальных чисел из списка
![]() ,
состоящего из
,
состоящего из
![]() чисел. Сначала мы разделим
чисел. Сначала мы разделим
![]() чисел на
чисел на
![]() групп, каждая по 5 элементов, будем искать
медиану в каждой из групп. Пусть
групп, каждая по 5 элементов, будем искать
медиану в каждой из групп. Пусть
![]() будет списком из
будет списком из
![]() медиан.
Рекурсивно ищем медиану
медиан.
Рекурсивно ищем медиану
![]() из списка
из списка
![]() .
Можно доказать, что
.
Можно доказать, что
![]() больше или равно хотя бы четверти чисел
в исходном списке
больше или равно хотя бы четверти чисел
в исходном списке
![]() и меньше либо равно хотя бы четверти
чисел в исходном списке
и меньше либо равно хотя бы четверти
чисел в исходном списке
![]() .
.
Следовательно,
число
![]() разделяет
список
разделяет
список
![]() на 2 подсписка
на 2 подсписка
![]() и
и
![]() ,
такие, что все числа в
,
такие, что все числа в
![]() меньше
или равны
меньше
или равны
![]() и все числа в
и все числа в![]() больше или равны
больше или равны
![]() .
Кроме этого, размер каждого из этих
двух подсписков минимально составляет
.
Кроме этого, размер каждого из этих
двух подсписков минимально составляет
![]() от начального списка
от начального списка![]() .
Теперь, если подсписок
.
Теперь, если подсписок
![]() включает
более
включает
более
![]() чисел, рекурсивно вызывается алгоритм
поиска
чисел, рекурсивно вызывается алгоритм
поиска
![]() минимальных чисел в списке
минимальных чисел в списке
![]() .
С другой стороны, если подсписок
.
С другой стороны, если подсписок![]() включает
включает
![]() чисел, таких что
чисел, таких что
![]() ,
рекурсивно вызывается алгоритм поиска
,
рекурсивно вызывается алгоритм поиска
![]() минимальных чисел в подсписке
минимальных чисел в подсписке
![]() .
В любом случае, из всей величины списка
мы обрабатываем максимум
.
В любом случае, из всей величины списка
мы обрабатываем максимум
![]() от начального списка
от начального списка
![]() .
Детали обсуждения алгоритма здесь
опускаются. Проведем анализ выше
описанного алгоритма поиска медианы.
.
Детали обсуждения алгоритма здесь
опускаются. Проведем анализ выше
описанного алгоритма поиска медианы.
Допустим,
что временная сложность алгоритма от
входных данных размера
![]() есть
есть
![]() .
Тогда поиск медианы из списка
.
Тогда поиск медианы из списка![]() ,
который состоит из
,
который состоит из
![]() медиан, потребует время
медиан, потребует время
![]() .
После для обоих списков
.
После для обоих списков![]() и
и![]() ,
максимальный размер которых составляет
,
максимальный размер которых составляет
![]() ,
поиск
,
поиск
![]() минимальных чисел в списке
минимальных чисел в списке![]() или
поиск
или
поиск
![]() минимальных чисел в списке
минимальных чисел в списке
![]() потребует время максимально равное
потребует время максимально равное
![]() .
Также понятно, что остальной расчет
может быть сделан за время
.
Также понятно, что остальной расчет
может быть сделан за время
![]() ,
где
,
где
![]() .
Следовательно, функция
.
Следовательно, функция![]() удовлетворяет следующему соотношению:
удовлетворяет следующему соотношению:
![]()
Имеется![]() -
целое, т.ч.
-
целое, т.ч.
![]() и
и
![]() ,из
чего несложно удостовериться по индукции
в том, что
,из
чего несложно удостовериться по индукции
в том, что
![]()
Таким
образом![]() .
.
Неформально основная идея алгоритма поиска и отсечения может быть описана следующим образом:
Алгоритм отсечения и поиска
Входные
данные: Задача
![]() размера
размера
![]()
Выходные
данные:
Решение
![]() этой задачи
этой задачи
НАЧАЛО
-
Если размер
 задачи
задачи
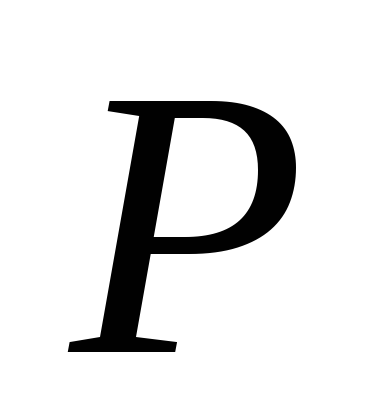 – небольшой, непосредственно решаем
– небольшой, непосредственно решаем
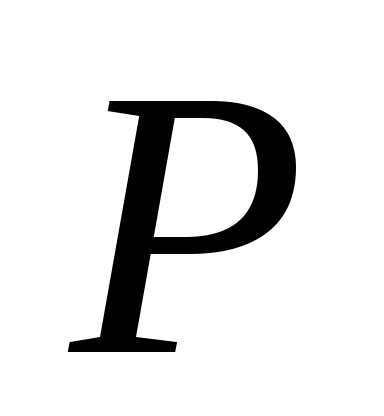 и останавливаемся.
и останавливаемся. -
Разделение задачи
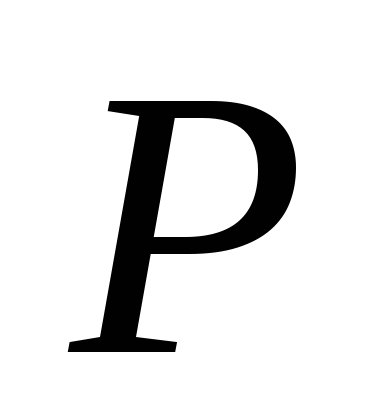 на
на
 небольших задач
небольших задач ,
размера
,
размера
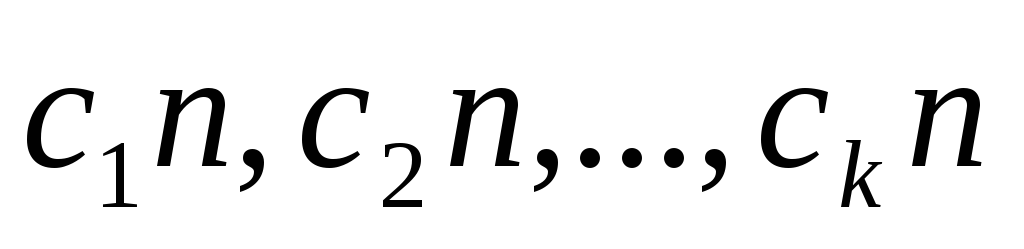 таким образом, что
таким образом, что
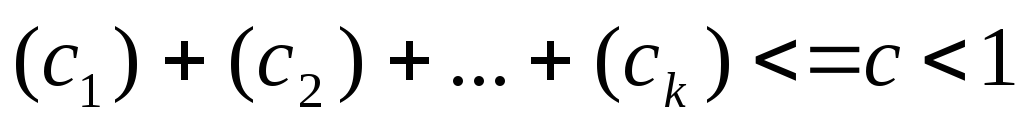 .
.
Здесь
![]() -
фиксированная константа.
-
фиксированная константа.
-
Рекурсивное решение задач
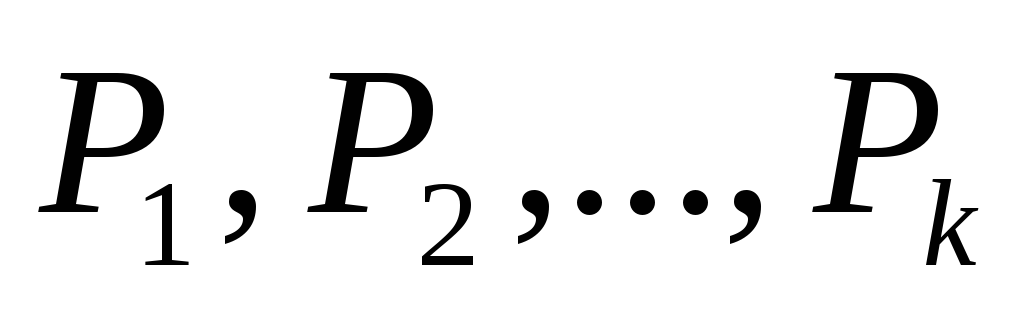 .
. -
После обработки результатов выполнения Шага 2 получаем решение задачи
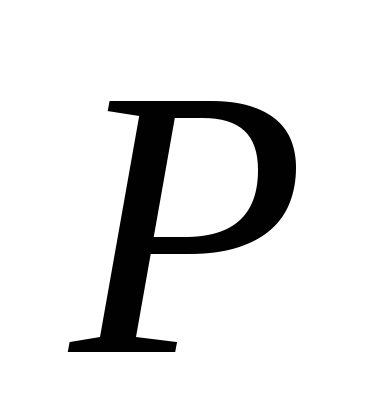 .
.
КОНЕЦ
Допустим,
что временная сложность алгоритма
Отсечения и Поиска
составляет
![]() и что Шаг1 и Шаг3 алгоритма потребуют
время
и что Шаг1 и Шаг3 алгоритма потребуют
время
![]() .
Тогда функция
.
Тогда функция
![]() может быть представлена как следующее
соотношение:
может быть представлена как следующее
соотношение:
![]()
Временная
сложность
![]() алгоритма
Отсечения и Поиска
может быть получена при решении ранее
приведенных соотношений. В частности,
если функция
алгоритма
Отсечения и Поиска
может быть получена при решении ранее
приведенных соотношений. В частности,
если функция
![]() является
является
![]() ,
тогда можно также доказать, что функция
,
тогда можно также доказать, что функция
![]() также
есть
также
есть![]() .
.
Алгоритм построения выпуклой оболочки
(Киркпатрика – Сайделя).
Представим алгоритм Отсечения и Поиска для построения выпуклой оболочки, которым обязаны Киркпатрику и Сайделю. Рассмотрим сначала следующую задачу:
