
- •16. Дифференциальные уравнения
- •16.1. Обыкновенные дифференциальные уравнения
- •13.2. Задачи, приводящие к дифференциальным уравнениям .
- •13.3. Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения однородные относительно переменных
- •Линейные дифференциальные уравнения
- •Уравнение Бернулли
- •13.4. Дифференциальные уравнения второго порядка
- •13.5. Уравнения второго порядка, допускающие понижение порядка
- •13.6. Линейные дифференциальные уравнения второго порядка
- •Метод вариации произвольных постоянных
- •13.7. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •13.8. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •13.9. Решение дифференциальных уравнений с помощью рядов.
- •Сводная таблица по теме: «Дифференциальные уравнения»
- •Решение практических задач
Решение практических задач
П р и м е р 13.1. Найти общий интеграл уравнения
 .
.
Решение. Разделим переменные в данном уравнении, поделив обе части на выражение cos2 y∙sin2 x:
 .
.
Интегрируя обе части данного уравнения, получим
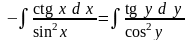 ,
,
откуда

Воспользуемся
тем, что С
– произвольная постоянная и заменим С
на
 .
Тогда
.
Тогда
 .
.
Это и есть общий интеграл данного уравнения.
П р и м е р 13.2. Найти общий интеграл уравнения
 .
.
Решение. Разрешим уравнение относительно производной :
 .
.
Поделив числитель и знаменатель правой части уравнения на х2, получим:

т. е. у есть функция отношения . Это означает, что данное уравнение – однородное.
Для решения этого
уравнения введем новую функцию
.
Тогда у
= ux
и
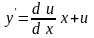 .
Тогда уравнение преобразуется в уравнение
с разделяющимися переменными:
.
Тогда уравнение преобразуется в уравнение
с разделяющимися переменными:

Интегрируя это уравнение, получим
 откуда
откуда
 .
.
Заменяя в последнем равенстве u отношением , окончательно получим:
 .
.
П р и м е р 13.3. Найти общее решение уравнения
 .
.
Решение. Положим y = u∙v, тогда y = u v + u v и данное уравнение примет вид:
 .
.
Решая уравнение
 ,
получим простейшее частное решение:
,
получим простейшее частное решение:
 .
.
Подставляя v в уравнение, получим
 .
.
из которого находим u:

Итак, искомое общее решение примет вид
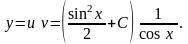
П р и м е р 13.4. Найти общее решение уравнения
 .
.
Решение. 1) Найдем решение соответствующего однородного уравнения. Для этого составим характеристическое уравнение, т. е. y = k2, y = k:
 .
.
Следовательно,
 .
.
2) Найдем теперь
у*.
Здесь правая часть имеет вид
 ,
где k
= – 3, Pn(x)
= A.
Так как k
= – 3 является двукратным корнем
характеристического уравнения, т. е. r
= 2, то частное решение у*
следует искать в форме
,
где k
= – 3, Pn(x)
= A.
Так как k
= – 3 является двукратным корнем
характеристического уравнения, т. е. r
= 2, то частное решение у*
следует искать в форме
 ,
,
где А
– коэффициент, подлежащий определению.
Вычислим производные
 и
и
 :
:
 ;
;
 .
.
Подставляя выражения
для у*,
и
в данное выражение, сокращая обе части
на
 и приводя подобные члены, в итоге получим
2 А
= 14, откуда А
= 7. Следовательно, искомое частное
решение имеет вид:
и приводя подобные члены, в итоге получим
2 А
= 14, откуда А
= 7. Следовательно, искомое частное
решение имеет вид:

Итак, общее решение данного уравнения

Пример
13.5. .
Найти три первых, отличных от нуля, члена
разложения в степенной ряд решения
 дифференциального уравнения
дифференциального уравнения
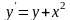 ,
удовлетворяющего начальному условию
,
удовлетворяющего начальному условию
 .
.
Решение. Представим решение данного уравнения в виде ряда
 .
(*)
.
(*)
Подставив
начальное условие
 ,
,
 в (*), получим
в (*), получим
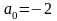 .
Продифференцируем разложение (*):
.
Продифференцируем разложение (*):
 .
(**)
.
(**)
Подставим
в данное дифференциальное уравнение
вместо
 его
значение (**), а вместо
его
значение (**), а вместо
 – его выражение (*), взяв первые три члена
(в соответствии с условием задачи).
Получим
– его выражение (*), взяв первые три члена
(в соответствии с условием задачи).
Получим
 .
Приравнивая коэффициенты при одинаковых
степенях
.
Приравнивая коэффициенты при одинаковых
степенях
 слева и справа последнего равенства,
получим
слева и справа последнего равенства,
получим
 ,
,
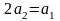 .
Так как
,
то
.
Так как
,
то
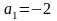 ,
,
 ,
и решение (8) примет вид
,
и решение (8) примет вид
 .
.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
13.1. Найти общие интегралы уравнений:
а) x + x y + y (y + x y) = 0;
б) x2 y + y = 0;
в) x2 + y2 – 2 x y y = 0;
г) x y + y = ln x + 1;
13.2. Найти частные интегралы по данным начальным условиям:
а) y = (2 y + 1) ctg x, y (π/4) = 0,5.
б)
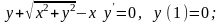
в)
 .
.
13.3. Решить уравнения:
а) x3 y + x2 y = 1;
б) y + y tg x = sin 2 x;
в) y y + y 2 = 0;
13.4. Решить уравнения:
а) y – 2 y + y = e2 x;
б) y – 2 y = x e– x;
в) y + 3 y + 2 y = sin 2 x + 2 cos 2 x.
