15. Элементы теории функций комплексного переменного
15.1. Комплексные числа, действия над ними
Определение. Комплексным числом z называется число вида
z=x+iy, (15.1)
где
x,
y
;
– мнимая
единица.
Числа x и y называются соответственно действительной и мнимой частями комплексного числа z, для них приняты обозначения:
x= Re (x + iy) = Re z; y = Im (x + iy )= Im z.
Если x=0, то число 0 + iy = iy называется чисто мнимым.
Если y=0, то число x + i0=x отождествляется с действительным числом x, т. е. любое действительное число можно рассматривать как комплексное. Множество комплексных чисел обозначается С.
Следовательно,
множество действительных чисел содержится
во множестве комплексных чисел R
C.
Форма записи комплексного числа в виде (15.1) называется алгебраической.
Комплексное число z=0 + 0i называется нулем. Понятия «больше» и «меньше» для комплексных чисел не определены.
Определение.
Комплексное число
=x-iy
называется сопряженным с числом z=x+
iy.
Два комплексных числа, которые отличаются
только знаком мнимой части, т.е. z=x+
iy
и
=x-iy,
называются комплексно-сопряженными.
Комплексное
число z=x+
iy
изображается
в плоскости xOy
или точкой
с координатами (x,
y),
или как вектор
,
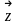с проекциями на оси абсцисс и ординат
равными соответственно x
и
y
Длина
r
вектора
называется модулем числа z
и обозначается
.
(15.2)
Плоскость xOy называется комплексной плоскостью, ось абсцисс - действительной осью, ось ординат – мнимой осью.
Угол
между положительным направлением оси
Ox
и вектором
называется
аргументом z
и обозначается Arg
z,
он определяется с точностью до слагаемого,
кратного 2.
где
arg
z
– главное значение аргумента.
Тригонометрическая форма комплексного числа имеет вид
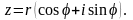(15.3)
Связь между алгебраической и тригонометрической формами:
(15.4)
Чтобы перейти от алгебраической формы комплексного числа к тригонометрической, надо найти его модуль по формуле (15.2), а затем с помощью одной из формул (15.4) найти аргумент .
Для главного значения аргумента справедливо
|
|
|
|
|
;
;
(15.5)
.Если
комплексное число z
находится на одной из осей, то
находят непосредственно. Например,
.
Тогда
.
Показательная форма комплексного числа наиболее удобная его форма. Для ее получения применяют формулу Эйлера:
,
(15.6)
(е =2,718 … иррациональное число).
Если комплексное число z записано в тригонометрической форме (15.3), то используя формулу (15.6), получим показательную форму комплексного числа:
,
(15.7)
где
;
.
Действия над комплексными числами производятся так:
а) числа заданы в алгебраической форме:
если
то
;
(15.8)
,
(15.9)
(при
z2≠0);
(15.10)
Действия над комплексными числами в алгебраической форме выполняются по тем же правилам, что и над многочленами с действительными коэффициентами, если учесть, что
,
,
,
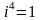и т. д.
Частное
получается при умножении числителя и
знаменателя дроби
на число
,
комплексно-сопряженное знаменателю.
Возведение
комплексного числа z
в степень n
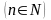рассматривается
как умножение
z
на себя n
раз. Например,
б) числа заданы в тригонометрической форме:
если
,
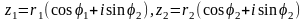то
,
(15.11)
(при
z2≠
0); (15.12)
если
то
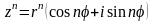– формула Муавра;
;
(15.13)
в) числа заданы в показательной:
если
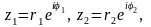то
;
(15.14)
если
то
;
(15.15)
если
то
,
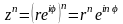(15.16)
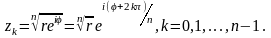(15.17)
Для взаимно сопряженных чисел z и справедливы формулы:
если
,
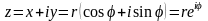то
.