7. Задача экономичного размера заказа с разрывами цен.

Обозначения:

у — объем заказа (количество единиц продукции),

D — интенсивность спроса (измеряется в ед-цах продукции на ед-цу времени),

t₀ — продолжительность цикла заказа (измеряется во временных единицах),

К— затраты на оформление, связанные с размещением заказа,

h — затраты на хранение (затраты на ед-цу складируемой продукции в ед-цу времени).

Предположим, что есть скидка при больших объемах заказов:

–q-порог скидки, где с₁>с₂.

Затраты на приобретение:

Так как цена при разных объемах разная, то можно учесть ее в общей функции затрат:

Решение о том, воспользоваться скидкой или нет зависит от того, в какой из трех областей расположена величина порога скидки:

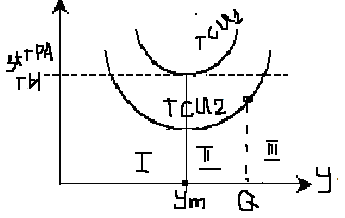
Величина Q – порог эффективности скидки (экономия от скидки съедается затратами на хранение) определяется из уравнения TCU₂(Q)=TCU₁(y_т).

17. [0,ym]-скидку уже получили

[ym,Q]-будем пользоваться

[Q,бесконечность)-нет

Оптимальное значение y*:

8.Многопродуктовая статическая модель управления запасами с ограничением вместимости.

Эта модель рассматривает задачу управления запасами п различных товаров, которые хранятся на одном складе ограниченной вместимости. Хар-ся постоянным во времени спросом, мгн.пополн-ем запаса и отсут-ем дефицита.

Определим для товара i, i=1,2,...,n, следующие параметры.

D_i— интенсивность спроса,

K_i — стоимость размещения заказа,

h_i — стоимость хранения единицы товара в единицу времени,

у_i — объем заказа,

a_i — объем, место, занимаемое на складе единицы товара,

А — максимальное складское пространство для хранения товаров n видов.

Математическая модель сформулированной задачи имеет следующий вид:

при ограничениях:

Алгоритм решения этой задачи можно описать следующим образом.

Шаг 1. Вычисляются оптимальные объемы заказов без учета ограничения по вместимости склада:

Шаг2. Проверяем, удовлетворяют ли значения у* ограничению по вместимости склада. Если "Да", то решение найдено. Иначе - шаг 3.

Шаг 3. Ограничение по вместимости склада должно выполняться в форме равенства. Для решения строим функцию Лагранжа:

Множитель Лагранжа<0. Функция Лагранжа по определению является выпуклой, поэтому оптимальное значение получаем путем приравнивания к нулю первых частных производных.

- таких выражений n штук.

Из первого Общего метода не существует, поэтому данная система решается численным методом. Так как лямбда<0, то последовательно ее уменьшаем с малым шагом до тех пор, пока найденное значение yi не удовлетворит ограничению по вместимости склада.

9. Динамическая модель управления запасами при отсутствии затрат на оформление.

В данной модели объем спроса на протяжении периода хотя и известен (является детерминированным), но он динамический, поскольку может периодически меняться.

Данная модель применяется в календарном планировании производства, где есть явно выделенные циклы (периоды) производства. Всего n равных периодов. Возможные объемы производства ограничены в каждом из периодов, могут включать несколько уровней - при сверхурочном режиме и обычном.

Основные предположения:

1)Отсутствие затрат на оформление заказов

2)недопустимость дефицита

3)Стоимость производства единицы продукции в любой период либо является постоянной, либо содержит возрастающие предельные затраты (каждый новый уровень увеличивает затраты, то есть функция затрат является выпуклой)

4)Стоимость хранения единицы продукции является постоянной величиной в каждый период.

Показано на рис, как производственные затраты на единицу продукции растут с увеличением уровня производства.

Данную задачу можно сформулировать как транспортную с числом пунктов отправления n*k, n потребителями и k способами (уровнями) выполнить заданный объем работы. В качестве стоимости перевозка берется сумма затрат используемого производственного процесса и стоимости хранения в соответствующие периоды. Оптимальное решение этой задачи определит объемы производства продукции для каждого уровня, которые минимизируют суммарные затраты на производство и хранение.