5.Обобщенная модель управления запасами.

Мало запасов может привести к остановке основного вида деятельности, а излишек запасов вызывает проблему хранения. Задачи управления запасами могут быть детерминированными или вероятностными.

Основная цель – баланс между риском недостачи и затратами на их хранение. Природа задачи управления запасами определяется неоднократным размещением и получением заказов заданных объемов продукции, которая в дальнейшем будет представлять собой хранимые запасы. Размещение запасов при этом происходит в определенный момент времени.

Стратегия управления запасами отвечает на вопросы:

1. Какое количество продукции заказывать?

2. Когда заказывать?

Ответ на первый вопрос определяет экономичный размер заказа, для чего необходимо минимизировать функцию затрат:

(суммарные затраты системы управления запасами) = (затраты на приобретение) + (затраты на оформление заказа) + (затраты на хранение) + (потери от дефицита запасов)

Оптимальный уровень запаса соответствует минимуму суммарных затрат.

Все эти затраты д.б. выражены как функции искомого объема заказа и интервалы времени между заказами.

1)Затраты на приобретение: опред-ся стоимостью единицы приобретаемой продукции.

2)Затраты на оформление: постоянные расходы, связанные с размещением заказов, не зависят от объема заказов.

3)Затраты на хранение: это затраты на содержание запасов на складе: сюда обычно включается стоимость хранения, содержания и ухода, а также процентно-инвестиционный капитал.

4)Потери от дефицита: явные потери, связанные с выплатой неустойки; неявные и неформализованные (потери доверия клиента)

Ответ на второй вопрос зависит от типа управления запасами. 2 типа проверок:

1)периодический контроль (инвентаризация) через равные промежутки времени, то момент поступления заказа совпадает с началом периода.

2)непрерывный контроль, новый заказ размещается, если уровень запаса опускается до заранее определенного значения, которое называется точкой возобновления заказа.

6. Классическая статическая модель.

Модель управления запасами простейшего типа характеризуются постоянным во времени спросом, мгновенным пополнением запаса и отсутствием дефицита.

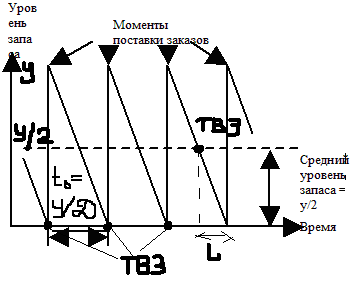
Рисунок Изменение уровня запаса во времени

y- объем заказа.

D- интенсивность спроса (единица продукции / единица времени). Наивысшего уровня запас достигается в момент поставки заказа – y. Уровень запаса достигает нуля спустя t0=y/D единиц времени после получения заказа размером y.

Пусть К – затраты на оформление заказа, имеющие место всякий раз при его размещении и затраты на хранение единицы заказа в единицу времени равны h. Cуммарные затраты в единицу времени TCU(y) как функцию от Yможно представить в виде:

.

Продолжительность цикла движения заказа составляет t₀=y/D и средний уровень запаса равен y/2.

. Оптимальное значение размера заказа: .

Оптимальная стратегия модели предусматривает заказ у^* единиц продукции через каждые t₀^*=y^*/D единиц времени.

Предположим, что на пополнение запасов требуется некоторое время: срок выполнения заказа (чистое запаздывание) L от момента размещения заказа до его поставки. Сдвигаем ТВЗ(Точку возобновления заказов) на величину L.

Если L < t₀^*, то ТВЗ=L*D.

Если это условие не выполняется, вычисляют эффективный срок поставки: , ([]-целая часть). ТВЗ=Le*D.